Реферат по теме выпускной работы
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Обзор исследований и разработок
- 3.1 Точные алгоритмы
- 3.2 Эвристические алгоритмы
- 3.3 Алгоритмы поиска
- 3.4 Обобщенные результаты
- 4. Обзор существующих систем
- 5. Описание задачи оптимизации пути
- 6. Математическая постановка задачи
- Выводы
- Список источников
Введение
Текущий уровень развития технологий обуславливает повсеместное применение грузоперевозок на предприятиях, осуществляющих различные виды деятельности. В текущее время наиболее распространенными являются автомобильные грузоперевозки, по причине как относительной дешевизны, так и возможности транспортировки груза напрямую из точки погрузки к адресату или пункту выгрузки благодаря достаточно разветвленной сети автомобильных дорог. Однако не все предприятия способны иметь в своем составе грузовой автопарк и сопутствующую инфраструктуру, в связи с чем успешно функционируют специализированные предприятия, называемые транспортными компаниями.
Транспортная компания осуществляет перевозку грузов между различными пунктами для различных заказчиков. Для осуществления такой деятельности в компании имеется соответствующая инфраструктура и ведется учет работы с использованием программных средств. На сегодняшний день развитие транспортных компаний и увеличение их количества происходит высокими темпами, в связи с чем усиливается конкуренция и появляется необходимость оптимизации работы транспортной компании с целью уменьшения затрат и увеличения прибыли [1].
1. Актуальность темы
Оптимизация работы транспортной компании подразумевает сокращение расходов на перевозку груза, требует длительных арифметических вычислений, поэтому производится с использованием специальных программных средств, называемых логистическими системами. Каждая из логистических систем использует свои собственные алгоритмы для оптимизации работы, причем эти алгоритмы скрыты от конечного пользователя системы. В текущее время существует большое количество логистических систем, каждая из которых предоставляет свой, отличный от других, функционал, учитывая при этом большое количество факторов [2]. Однако быстрое развитие транспортных компаний обуславливает постоянное изменение условий их работы, появление новых факторов, которые не в полной мере учитываются существующими логистическими системами.
Алгоритмы существующих логистических систем зачастую не адаптированы к постоянно изменяющимся условиям работы транспортной компании, в связи с чем все более актуальной становится необходимость модификации этих алгоритмов а также разработки новых алгоритмов, учитывающих все факторы, влияющие на работу транспортных компаний в настоящее время.
2. Цель и задачи исследования
Целью исследования является оптимизация работы транспортной компании за счет уменьшения затрат на перевозку грузов путем применения модифицированных алгоритмов для решения транспортных задач с учетом ограничений на несколько пунктов погрузки и различную грузоподъемность транспортных средств.
Основные задачи исследования:
- Провести анализ существующих алгоритмов, методов и технологий решения транспортной задачи;
- Разработать математическую модель перевозки грузов транспортными средствами с учетом ограничений на множество различных пунктов погрузки и различную грузоподъемность транспортных средств;
- Разработать модифицированный алгоритм решения транспортной задачи с учетом вышеперечисленных ограничений;
- Экспериментально проверить эффективность работы алгоритма.
3. Обзор исследований и разработок
Для решения задач коммивояжера и задачи о загрузке используются алгоритмы, которые можно отнести к трем группам: точные алгоритмы, эвристические алгоритмы и алгоритмы поиска. При этом для практического применения в условиях большой размерности задачи преимущественно используются эвристические алгоритмы и алгоритмы поиска, как наиболее экономичные с точки зрения временных ресурсов и вычислительных ресурсов компьютера.
3.1 Точные алгоритмы
Среди точных алгоритмов наиболее популярными для решения задачи коммивояжёра являются:
- алгоритм полного перебора;
- метод ветвей и границ;
- метод последовательной сепарации.
Без учёта условия незамкнутости ограничения для задачи коммивояжёра полностью совпадают с ограничениями задачи о назначениях, которая достаточно эффективно решается методом последовательной сепарации. Алгоритм решения можно описать следующим образом. Решается задача о назначениях. Полученное решение:
- либо представляет замкнутый маршрут, включающий все города
- либо представляет совокупность нескольких замкнутых локальных маршрутов.
Первый случай представляет собой и решение задачи коммивояжёра, т.е. решение задачи о назначениях даёт одновременно решение задачи коммивояжёра. Для получения требуемого решения из второго случая следует разорвать замкнутые ветви и соединить их в один замкнутый маршрут наименьшей стоимости.
Алгоритм полного перебора осуществляет поиск в пространстве N! решений посредством перебора всех вариантов. Результатом работы алгоритма является точное решение. Недостатком алгоритма является его временная сложность – пространство поиска растёт экспоненциально, поэтому, когда N не является значительно малым, используют эвристические и поисковые алгоритмы. К преимуществам данного алгоритма можно отнести возможность распараллеливания и точное решение задачи [8].
Метод ветвей и границ является модификацией алгоритма полного перебора. Его суть заключается в добавлении проверки критерия ограничивающей функции, исходящего из знания задачи, по которому на определённом уровне можно приостановить построение данной ветви дерева перестановок. Он сохраняет все положительные свойства алгоритма полного перебора, но тем не менее мало пригоден для задач, где N не является значительно малым. В основе метода лежат следующие этапы:
- вычисление нижней границы (оценки);
- разбиение на подмножества, т.е. ветвление;
- расчёт оценок;
- нахождение решений;
- определение признака оптимальности;
- оценка точности приближённого решения.
3.2 Эвристические алгоритмы
Эвристические алгоритмы эффективны как при решении обобщённой задачи коммивояжёра, так и при решении простой задачи коммивояжёра. К ним можно отнести довольно большое количество методов:
- BV–метод;
- метод включения дальнего;
- метод имитации отжига;
- метод ближайшего соседа;
- нейронные сети.
Более подробно будут рассмотрены два метода: BV–метод и метод включения дальнего.
Идея метода включения дальнего заключается в следующем: пункты, максимально удаленные друг от друга, никогда не будут смежными в цепи [5]. Эти два пункта и будут базовыми для дальнейшего решения. Затем опять находится вершина, максимально удаленная от вершин, уже заключенных в цепь. Находится минимальная сумма длин рёбер между найденной вершиной и парой смежных вершин в цепи, что задает место в цепи найденной вершине. Данный алгоритм имеет линейную сложность, даёт приблизительное решение задачи и не может быть распараллелен.
BV–метод основан на анализе имеющегося эталонного маршрута и его оптимизации. Алгоритм условно состоит из трёх этапов:
- получение начального эталонного решения;
- построение BV матрицы;
- оптимизация текущего решения.
Начальное решение представляет собой лучшее решение из всех решений полученных на основе «жадного» метода. Для его реализации строится N маршрутов, по количеству пунктов доставки. В каждом из этих N маршрутов, начальный пункт равен номеру маршрута, а все последующие пункты выбираются по принципу жадного алгоритма (выбирается ближайший пункт).
Далее, как уже было сказано выше, среди них выбирается наилучший маршрут, т. е., с наименьшей длиной пути и он помечается как эталонный.
Второй этап алгоритма – построение BV–матрицы. Для этого строится матрица оценок размером NхN, первоначально заполненная нулями. Далее просматривая N построенных «жадных» маршрутов, для каждой пары соседних пунктов p и q, соответствующий элемент матрицы оценок a [p, q] увеличивается на единицу.
Третий этап алгоритма состоит в преобразовании эталонного маршрута с помощью последовательного применения BV–модификаторов к каждой паре пунктов, которым соответствует ненулевой элемент матрицы оценок. Если преобразованный маршрут имеет меньшую длину пути, то он становится эталонным и в матрице оценок соответствующий элемент заменяется на 0. Проход по BV–матрице повторяется до тех пор, пока модифицированный маршрут имеет превосходство над эталоном. Отсутствие превосходства модифицированного маршрута над эталоном, говорит о том, что полученное решение является конечным для данного метода решения.
BV–модификаторы могут быть следующих видов:
- модификатор
Сглаживания
; - модификатор
Перенос
; - модификатор
Инверсный переход
; - модификатор
Инверсный перенос
.
3.3 Алгоритмы поиска
Алгоритмы поиска являются наиболее распространёнными среди алгоритмов для решения задачи коммивояжёра. Лидерами среди них являются генетические алгоритмы и алгоритмы колонии муравьёв, или муравьиные алгоритмы. Изучим их более детально.
Генетические алгоритмы – это процедуры поиска, основанные на механизмах естественного отбора и наследования. В них используется эволюционный принцип выживания наиболее приспособленных особей. Они отличаются от традиционных методов оптимизации несколькими базовыми элементами [3][4]. В частности, генетические алгоритмы обладают рядом отличительных свойств:
- кодирование параметров – генетические алгоритмы обрабатывают не значения параметров самой задачи, а их закодированную форму;
- операции на популяции – генетические алгоритмы осуществляют поиск решения исходя не из единственной точки (начальное приближение), а из некоторой популяции;
- использование минимума информации о функции – генетические алгоритмы используют только целевую функцию, а не производные либо иную дополнительную информацию;
- рандомизация операций – генетические алгоритмы применяют вероятностные, а не детерминированные правила выбора.
Генетические алгоритмы являются наиболее оптимальными среди поисковых в плане соотношения время/качество и могут быть распараллелены [8].
Идея муравьиных алгоритмов – моделирование поведения колонии муравьёв, связанного с их способностью быстро находить кратчайший путь от муравейника к источнику пищи и адаптироваться к изменяющимся условиям, находя новый кратчайший путь. При своём движении муравей оставляет за собой дорожку феромонов, и эта информация используется другими муравьями для выбора пути. Это элементарное правило поведения и определяет способность муравьёв находить новый путь, если старый оказывается недоступным.
Если промоделировать процесс такого поведения на некотором графе, рёбра которого представляют собой возможные пути перемещения муравьёв в течение определённого времени, то наиболее обогащённый феромоном путь по рёбрам этого графа и будет являться решением задачи, полученным с помощью муравьиного алгоритма [6].
3.4 Обобщенные результаты
Точные алгоритмы и методы дают точное решение, соответственно их погрешность минимальна, они могут быть распараллелены, что является важным фактором, однако они непригодны для решения задач с большим количеством вершин, при этом временные затраты являются неприемлемыми.
Эвристические алгоритмы и методы являются лидерами по быстродействию, соответственно скорость их работы не требует больших вычислительных ресурсов, однако они дают лишь приблизительное решение задачи, т.е. погрешность при их использовании достаточно велика. Кроме того, эвристические алгоритмы далеко не всегда поддаются распараллеливанию – в некоторых случаях распараллелить можно лишь конкретные этапы алгоритма, в других случаях вообще невозможно применить параллелизм при их использовании. Следовательно, применение эвристических алгоритмов для решения рассматриваемой задачи актуально лишь в случае, когда быстродействие является критичным параметром.
Алгоритмы поиска являются компромиссным решением между точными и эвристическими – результативность поисковых алгоритмов является удовлетворительной, т.к. в случае их использования и погрешность, и время выполнения стремятся к минимуму, в отличии от двух других классов алгоритмов, в которых оптимизации подлежит лишь один из вышеперечисленных критериев. При этом, для увеличения эффективности алгоритмов поиска их целесообразно комбинировать с другими, например, эвристическими методами [7].
4 Обзор существующих систем
В настоящее время существует большое количество логистических систем, каждая из которых предоставляет свой, отличный от других, функционал, учитывая при этом большое количество факторов.
- Муравьиная логистика
- ePROMIS Transportation & Logistics
- Gensoft Logistics ERP
- Interlogis ILS–Online
Муравьиная логистика – онлайн сервис для расчета оптимальных маршрутов доставки. Сервис предоставляется для бесплатного использования на пробный период, после чего требует покупки лицензии для использования, при этом количество точек в маршруте может быть ограничено в зависимости от типа лицензии, а количество маршрутов в день ограничено независимо от типа лицензии [9].
Transportation & Logitics является продуктом компании ePROMIS, которая специализируется на разработке и внедрении облачных программных решений для автоматизации управления всеми участками цепочки поставок: запасами, транспортом. Программа Transportation & Logitics специализируется на построении оптимальных маршрутов доставки товара [10].
Система Transportation & Logitics является платной и не предоставляет демо–версии для ознакомления.
Gensoft Logistics – это сервис управления транспортной логистикой для компаний, чей бизнес связан с доставкой грузов. Сервис позволяет создавать оптимальные маршруты и эффективно планировать загрузку водителей и курьеров. Сервис является бесплатным только для некоммерческого использования. В противном случае стоимость использования обсуждается при составлении договора [11].
ILS–Online – это веб–ориентированная система управления логистикой. Она автоматически распределяет работу между исполнителями и планирует оптимальные маршруты для доставки точно в срок и с минимальными затратами. С её помощью пользователь имеет возможность контролировать и при необходимости корректировать движение сотрудников в режиме реального времени [12].
5. Описание задачи оптимизации пути
Транспортная компания выполняет перевозки груза парком транспортных средств различной грузоподъемности и различного объема. Парк транспортных средств компании может быть разбит на несколько пунктов погрузки, следовательно, расстояния от различных пунктов погрузки для одного и того же пункта выгрузки будут различны. При этом каждый автомобиль может перевозить несколько грузов, при этом не менее одного и не более грузоподъемности этого транспортного средства.
Каждый груз доставляется в отдельное определенное место. Каждый груз имеет некий критический срок доставки к заказчику, при этом фактический срок доставки груза к заказчику не должен превышать критический срок. В зависимости от грузов, погруженных в одно транспортное средство, определяются пункты выгрузки, через которые должен пройти маршрут данного автомобиля.
Маршрут определяется порядком обхода точек выгрузки груза при условии, что начальной и конечной точкой маршрута является место погрузки, а точки выгрузки груза могут идти в любом порядке, однако необходимо принимать во внимание длину маршрутов между пунктами выгрузки и ограничение на сроки доставки груза. При этом затраты на преодоление пути для одного автомобиля определяются как произведение суммарной длины маршрута и стоимости перевозки груза данным транспортным средством на единицу расстояния [1].
Исходя из выше приведенных ограничений требуется определить такую загрузку транспортных средств и такие маршруты, при которых суммарные затраты на преодоление пути всеми автомобилями с грузом будут минимальны. Таким образом, в данной работе решается задача коммивояжера и частично задача о загрузке.
В ходе анализа грузоперевозок в условиях транспортной компании была разработана схема материальных и информационных потоков, приведенная на рисунке 1.
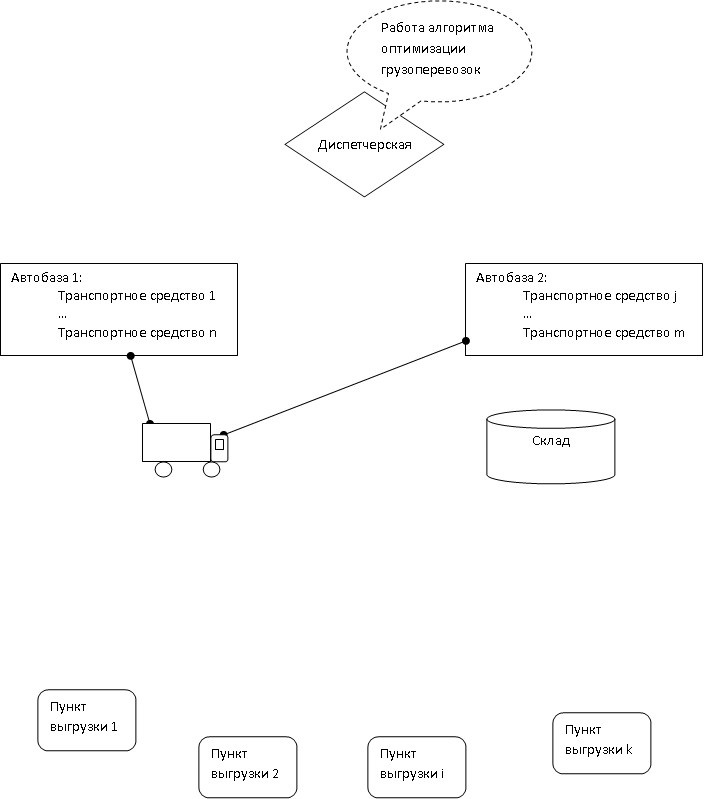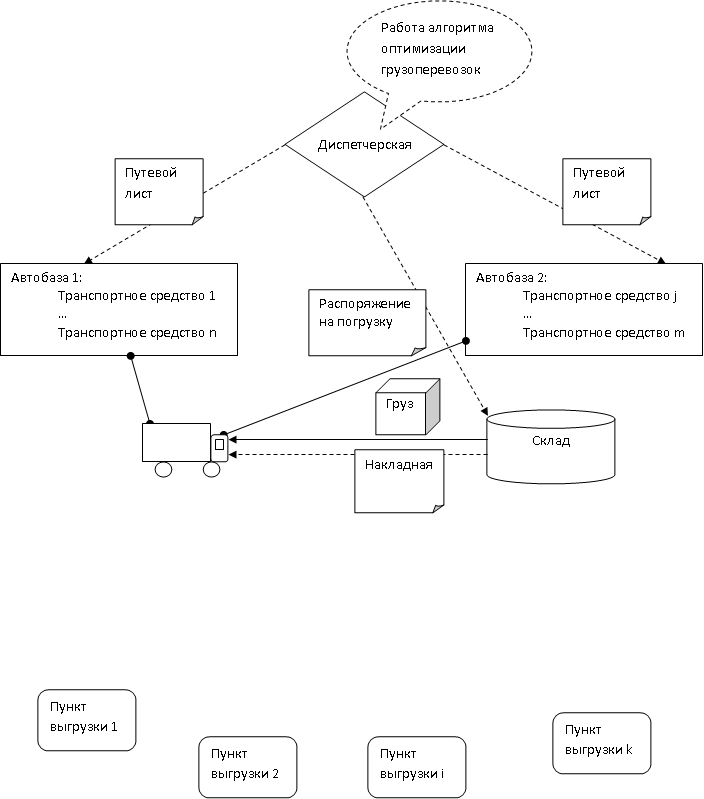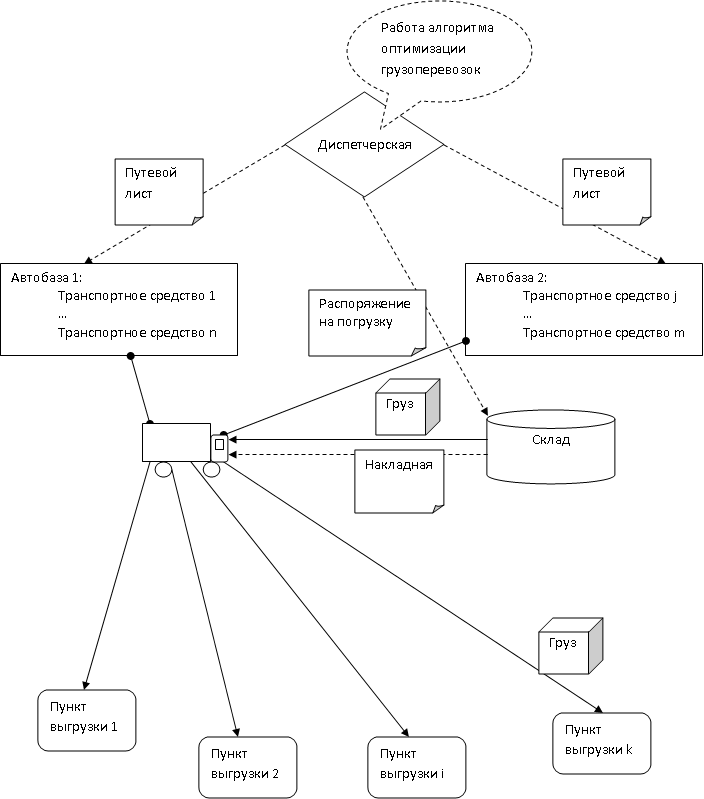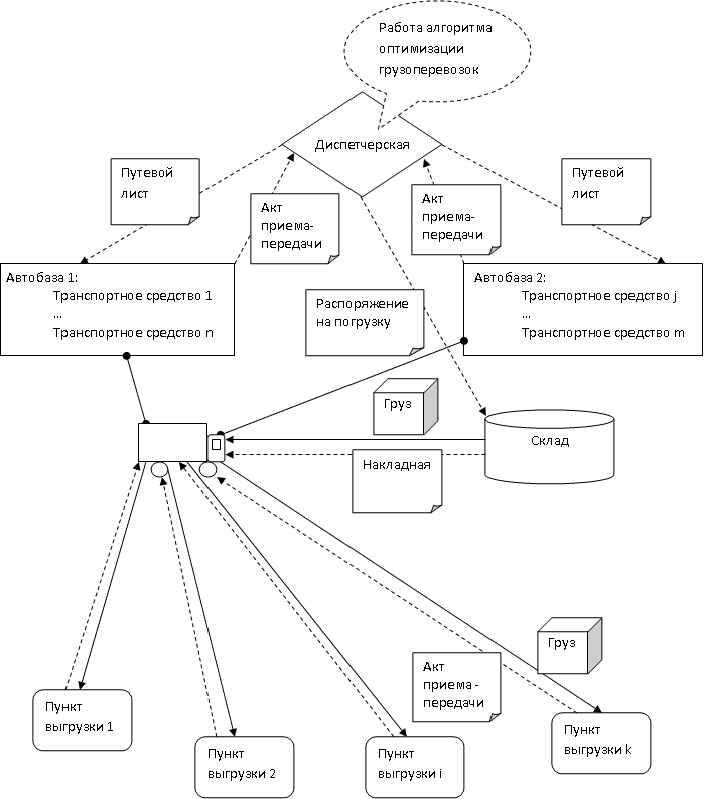
Рисунок 1 – Схема материальных и информационных потоков (анимация: 6 кадров, 5 циклов повторения, 64 килобайта)
На схеме материальные потоки(грузы) показаны сплошной линией, а информационные – прерывистой. Основными блоками являются диспетчерская, автобазы, транспортное средство, склад (пункт погрузки груза), пункты выгрузки.
Первым блоком в процессе грузоперевозок является диспетчерская. В диспетчерской формируются информационные потоки в автобазы в виде путевых листов для транспортных средств, находящихся в этих автобазах. Также диспетчерская формирует информационный поток для склада – распоряжение на погрузку. По завершении перевозки транспортным средством в диспетчерскую направляются информационные потоки в виде актов приема–передачи груза с автобаз. Именно в блоке диспетчерской предполагается работа алгоритма оптимизации грузоперевозок, выходными данными которого должны стать данные для путевых листов и распоряжения на погрузку.
Автомобиль с автобазы согласно данным из путевого листа направляется на склад, где получает груз и товарно–транспортную накладную. После погрузки автомобиль согласно путевому листу направляется в пункты разгрузки груза, очередность заезда в которые указана в путевом листе. При разгрузке автомобиля материальный поток груза направляется в пункт разгрузки, при этом в пункте разгрузки формируется информационный поток в виде акта приема–передачи груза, который направляется в автомобиль. По завершении рейса акты приема–передачи грузов через автобазу направляются в диспетчерскую.
При этом, поскольку транспортное средство движется через несколько пунктов разгрузки, пути между этими пунктами могут иметь различную длину в различных направлениях и при различном порядке следования, а при различной длине маршрутов изменяются также затраты на перевозку. В связи с этим необходимо оптимизировать грузоперевозки путем нахождения оптимального пути, то есть решить задачу коммивояжера.
6. Математическая постановка задачи
Данная задача оптимизации пути является частным случаем задачи коммивояжера, в котором присутствует разбиение на несколько начальных пунктов, в данном случае это пункты загрузки транспортных средств. Эти пункты расположены на различном удалении от пунктов выгрузки транспортных средств, таким образом, для каждого из пунктов загрузки необходимо составить свою собственную матрицу стоимости перевозок.
Целевая функция для всей системы определяется по формуле 1.
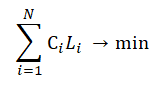 |
(1) |
где Ci – стоимость перевозки груза i–м автомобилем на единицу расстояния, Li – суммарная длина маршрута, по которому едет i–й автомобиль.
При этом необходимо учесть следующие ограничения, определяемые формулой 2.
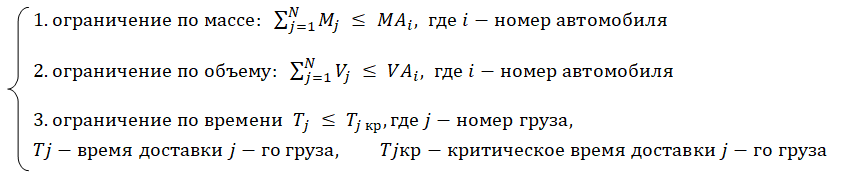 |
(2) |
При этом ограничение 1 определяет, что суммарная масса груза, перевозимого одним автомобилем, не может быть больше его грузоподъемности. Ограничение 2 определяет, что суммарный объем груза, перевозимого одним автомобилем, не может быть больше его объема. Ограничение 3 определяет, что время доставки груза в точку выгрузки должно быть не позднее некоторого T критического, которое задано в исходных данных.
Также необходимо учесть следующие дополнительные ограничения:
- грузоподъемность автомобилей различна
- пунктов отправки автомобилей несколько
- каждый груз может быть перевезен только одним автомобилем
- пункты выгрузки различны для каждого груза
Учитывая все вышеперечисленное, необходимо отметить, что рассматриваемая задача относится к задачам многокритериальной оптимизации. При объеме исходных данных 200 грузов в день и 10 транспортных средств для их перевозки область допустимых решений настолько велика, что время решения данной задачи точными методами невозможно за приемлемое время [13]. Применяемые ранее методы не лишены недостатков, в связи с чем требуются дальнейшие исследования даной темы.
Выводы
В ходе исследования был выполнен обзор алгоритмов для решения транспортных задач трех групп: точные, эвристические и поисковые. Был выполнен анализ найденных алгоритмов, их сравнение применимо к решению задачи коммивояжера с ограничениями на параметры транспортных средств, и несколько пунктов погрузки груза.
На основании анализа алгоритмов решения задач было определено, что ни один существующий алгоритм не решает задачу с учетом выше приведенных ограничений, что подтверждает актуальность исследования данной темы и разработки модифицированного алгоритма.
Было выполнено описание работы транспортной компании, представленное в виде схемы информационно–материальных потоков.
Была сформулирована и описана постановка задачи оптимизации грузоперевозок, определены целевая функция и ограничения данной задачи.
Замечания
На момент написания данного реферата магистерская работа еще не завершена. Предполагаемая дата завершения: май 2019 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Гарнов, А. П. Инструментарий логистики: учебник / А. П. Гарнов, Н. С. Киреева – М.:Креативная экономика, 2009. – 310 с.
- Товстик Т.М. Алгоритм приближенного решения задачи коммивояжера / Т.М. Товстик, Е.В. Жукова // Вестник СПбГУ. Серия 1. Математика. Механика. Астрономия. – СПБ:СПбГУ, 2013. – с. 101-106.
- Курейчик В.М. Генетический алгоритм решения логистической задачи / В.М. Курейчик, А.А. Рокотянский // Известия ЮФУ. Технические науки. – Таганрог:ТРТУ, 2012. – №136 –c. 245-251.
- Александрова О.А. Оптимизация грузовых перевозок с использованием генетических алгоритмов / О.А. Александрова, А.И. Секирин // Информатика и компьютерные технологии – 2009 №5, – Донецк: ДонНТУ, с. 237–244.
-
Борознов В.О. Исследование эвристического метода решения задачи коммивояжера / В.О. Борознов // Электронный научный журнал
ИССЛЕДОВАНО В РОССИИ
. – Москва:МФТИ, 2008. – с. 322-328. - Haroun S.A. A Performance Comparison of GA and ACO Applied to TSP / S.A. Haroun, B. Jamal, E.H. Hicham // International Journal of Computer Applications. – 2015. – vol.117 – pp. 28–35.
- Савкин В.Ю. Анализ методов решения задачи коммивояжера / В.Ю. Савкин, В.А. Светличная, Радзывыло К.Г. // Материалы IX Международной научно-технической конференции. – Донецк: ДонНТУ, 2018. – с.183–188.
- Скобцов Ю.А. Основы эволюционных вычислений. Донецк: ДонНТУ, 2008. – 326 с.
- Автоматизация транспортной логистики – онлайн сервис для планирования оптимальных маршрутов доставки [Электронный ресурс] – Режим доступа: https://ant-logistics.com/
- Transportation management software – ePROMIS ERP [Электронный ресурс] – Режим доступа: https://www.epromis.net/industries/transportation-logistics
- Gensoft – Logistics Software Provider [Электронный ресурс] – Режим доступа: http://www.gensoft.lk/
- Interlogis – Logistics Solutions for Business [Электронный ресурс] – Режим доступа: https://interlogix.com/
- Семенкина, О.Е. Effectiveness Comparison of Ant Colony and Genetic algorithms for solving combinatorial optimization problems // Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева. – 2012. – №1. – С.96-97.
