Факультет компьютерных наук и технологий
Кафедра компьютерной инженерии
Специальность «Программное обеспечение интеллектуальнных систем»
Разработка и проектирование программного обучающего модуля
Научный руководитель: д.ф.-м.н., проф. Миненко Александр Степанович
Так как генетические и эволюционные алгоритмы оптимизации являются алгоритмами случайно-направленного поиска и применяются в основном там, где сложно или невозможно сформулировать задачу в виде, пригодном для более быстрых алгоритмов локальной оптимизации (например, для градиентных алгоритмов, где возможно, вдобавок, «мгновенное» вычисление градиента представленной в виде нейронной сети функции с помощью алгоритма обратного распространения ошибки), либо если стоит задача оптимизации недифференцируемой функции или задача многоэкстремальной глобальной оптимизации, то их использование является очень актуальным, а для понимания принципа работы генетического алгоритма необходимо понимать как он работает и какую последовательность процессов в себя включает, что делает разработку обещающего модуля «Генетические алгоритмы» актуальным программным продуктом.
Создание обучающего модуля поможет студентам в изучении лекционного материала путём разделения обучающего материала на не большие теоретические блоки с последующем тестированием по пройденному учебному блоку. Так же разработанный программный продукт позволит преподавателю отслеживать пройденный материал студентов с возможностью просмотра результатов тестирования по каждому учебному блоку, а модуль администрации позволит легко изменить содержание учебных блоков при необходимости.
Разрабатываемый программный модуль является узкоспециализированным, так предназначен в большей мере для студентов, университетов, которые изучают дисциплину «генетические алгоритмы», и в дополнение к лекционным занятиям пользуется разрабатываемым модулем.
Данная разработка является актуальной, так как аналогов данному программному не было выявлено, что делает данную разработку перспективной в будущем.
Обучение с использованием компьютерных технологий рассматривается как способ обучения, не ограничивающий обучающего и обучающегося во времени или пространстве, но ограничивающий непосредственные контакты. Однако основная масса обучающихся, как правило, инертна и нуждается в постоянном «подталкивании». Над проблемой «подталкивания» работают многие ученые и разработчики обучающих программ, понимая, что самое эффективное – это комплексный подход, в который включаются все составляющие данного процесса: преподаватель – обучающая программа – обучающийся.
Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока поколения не перестанут существенно отличаться друг от друга, или не пройдет заданное количество поколений или заданное время. Для каждого поколения реализуются отбор, кроссовер (скрещивание) и мутация.
Шаг 1: генерируется начальная популяция, состоящая из N особей со случайными наборами признаков.
Шаг 2 (борьба за существование): вычисляется абсолютная приспособ-ленность каждой особи популяции к условиям среды f(i) и суммарная приспособленность особей популяции, характеризующая приспособленность всей популяции. Затем при пропорциональном отборе для каждой особи вычисляется ее относительный вклад в суммарную приспособленность популяции Ps(i), т.е. отношение ее абсолютной приспособленности f(i) к суммарной приспособленности всех особей популяции.
Поскольку количество потомства особи пропорционально ее приспособленности, то естественно считать, что если это количество информации:
- положительно, то данная особь выживает и дает потомство, численность которого пропорциональна этому количеству информации;
- равно нулю, то особь доживает до половозрелого возраста, но потомства не дает (его численность равна нулю);
-меньше нуля, то особь погибает до достижения половозрелого возраста.
Таким образом, можно сделать фундаментальный вывод, имеющий даже мировоззренческое звучание, о том, что естественный отбор представляет собой процесс генерации и накопления информации о выживании и продолжении рода в ряде поколений популяции, как системы.
Шаг 3: начало цикла смены поколений.
Шаг 4: начало цикла формирования нового поколения.
Шаг 5 (отбор): осуществляется пропорциональный отбор особей, которые могут участвовать в продолжении рода. Отбираются только те особи популяции, у которых количество информации в фенотипе и генотипе о выживании и продолжении рода положительно, причем вероятность выбора пропорциональна этому количеству информации.
Шаг 6 (кроссовер): отобранные для продолжения рода на предыдущем шаге особи с заданной вероятностью Pc подвергаются скрещиванию или кроссоверу (рекомбинации).
Шаг 7 (мутация): выполняются операторы мутации. При этом признаки потомков с вероятностью Pm случайным образом изменяются на другие. Отмечу, что использование механизма случайных мутаций роднит генетические алгоритмы с таким широко известным методом имитационного моделирования, как метод Монте-Карло.
Шаг 8 (борьба за существование): оценивается приспособленность потомков (по тому же алгоритму, что и на шаге 2).
Шаг 9: проверяется, все ли отобранные особи дали потомство.Если нет, то происходит переход на шаг 5 и продолжается формирование нового поколения, иначе – переход на следующий шаг 10.
Шаг 10: происходит смена поколений по следующему алгоритму:
- потомки помещаются в новое поколение;
- наиболее приспособленные особи из старого поколения переносятся в новое, причем для каждой из них это возможно не более заданного количества раз;
Шаг 11: проверяется выполнение условия останова генетического алгоритма. Выход из генетического алгоритма происходит либо тогда, когда новые поколения перестают существенно отличаться от предыдущих, т.е., как говорят, «алгоритм сходится», либо, когда пройдено заданное количество поколений или заданное время работы алгоритма (чтобы не было «зацикливания» и динамического зависания в случае, когда решение не может быть найдено в заданное время).
Введём основные понятия, применяемые в генетических алгоритмах.
Вектор – упорядоченный набор чисел, называемых компонентами вектора. Так как вектор можно представить в виде строки его координат, то в дальнейшем понятия вектора и строки считаются идентичными.
Булев вектор – вектор, компоненты которого принимают значения из двух элементного (булева) множества, например, {0, 1} или {−1, 1}.
Хеммингово расстояние – используется для булевых векторов и равно числу различающихся в обоих векторах компонент.
Хеммингово пространство – пространство булевых векторов, с введенным на нем расстоянием (метрикой) Хемминга. В случае булевых векторов размерности n рассматриваемое пространство представляет собой множество вершин n-мерного гиперкуба с хемминговой метрикой. Расстояние между двумя вершинами определяется длиной кратчайшего соединяющего их пути, измеренной вдоль ребер.
Хромосома –вектор (или строка) из каких-либо чисел. Если этот вектор представлен бинарной строкой из нулей и единиц, например, 1010011, то он получен либо с использованием двоичного кодирования, либо кода Грея.
Ген – позиция (бит) в хромосоме.
Индивидуум (генетический код, особь) – набор хромосом (вариант решения задачи). Обычно особь состоит из одной хромосомы, поэтому в дальнейшем особь и хромосома идентичные понятия.
Расстояние – хеммингово расстояние между бинарными хромосомами.
Кроссинговер ´ (кроссовер, скрещивание) – операция, при которой две хромосомы обмениваются своими частями. Например, 1100&1010 → 1110&1000.
Мутация – случайное изменение одной или нескольких позиций в хромосоме. Например, 1010011 → 1010001.
Инверсия – изменение порядка следования битов в хромосоме или в ее фрагменте. Например, 1100 → 0011.
Популяция – совокупность индивидуумов.
Пригодность (приспособленность) – критерий или функция, экстремум которой следует найти.
Локус – позиция гена в хромосоме.
Аллель – совокупность подряд идущих генов.
Эпистаз – влияние гена на пригодность индивидуума в зависимости от значения гена, присутствующего в другом месте. Ген считают эпистатическим, когда его присутствие подавляет влияние гена в другом локусе. Эпистатические гены из-за их влияния на другие гены иногда называют ингибирующими. Подавление проявления гена неаллельным ему геном называется гипостазом, а сам подавляемый ген – гипостатическим.
Основные операторы генетического алгоритма можно разбить на 3 группы:
- операторы выбора родителей (операторы отбора);
- операторы скрещивания (рекомбинации);
- мутация.
Панмиксия – самый простой оператор отбора. В соответствии с ним каждому члену популяции сопоставляется случайное целое число на отрезке [1; n], где n – количество особей в популяции.
Будем рассматривать эти числа как номера особей, которые примут участие в скрещивании. При таком выборе какие-то из членов популяции не будут участвовать в процессе размножения, так как образуют пару сами с собой. Какие-то члены популяции примут участие в процессе воспроизводства неоднократно с различными особями популяции.
Несмотря на простоту, такой подход универсален для решения различных классов задач. Однако он достаточно критичен к численности популяции, поскольку эффективность алгоритма, реализующего такой подход, снижается с ростом численности популяции.
Инбридинг представляет собой такой метод, когда первый родитель выбирается случайным образом, а вторым родителем является член популяции ближайший к первому. Здесь «ближайший» может пониматься, например, в смысле минимального расстояния Хемминга (для бинарных строк) или евклидова расстояния между двумя вещественными векторами. Расстояние Хемминга равно числу различающихся локусов (разрядов) в бинарной строке.
Инбридинг и аутбридинг по-разному влияют на поведение генетического алгоритма.
Так, инбридинг можно охарактеризовать свойством концентрации поиска в локальных узлах, что фактически приводит к разбиению популяции на отдельные локальные группы вокруг подозрительных на экстремум участков ландшафта.
Аутбридинг же направлен на предупреждение сходимости алгоритма к уже найденным решениям, заставляя алгоритм просматривать новые, неисследованные области.
Инбридинг и аутбридинг бывает генотипным (когда в качестве расстояния берется разность значений целевой функции для соответствующих особей) и фенотипным (в качестве расстояния берется расстояние Хемминга)
При турнирном отборе (tournament selection) из популяции, содержащей N особей, выбираются случайным образом t особей, и лучшая из них особь записывается в промежуточный массив (см. рис. 3.1). Эта операция повторяется N раз. Особи в полученном промежуточном массиве затем используются для скрещивания (также случайным образом). Размер группы строк, отбираемых для турнира, часто равен 2. В этом случае говорят о двоичном (парном) турнире. Вообще же t называют численностью турнира.
Преимуществом данного способа является то, что он не требует дополнительных вычислений.
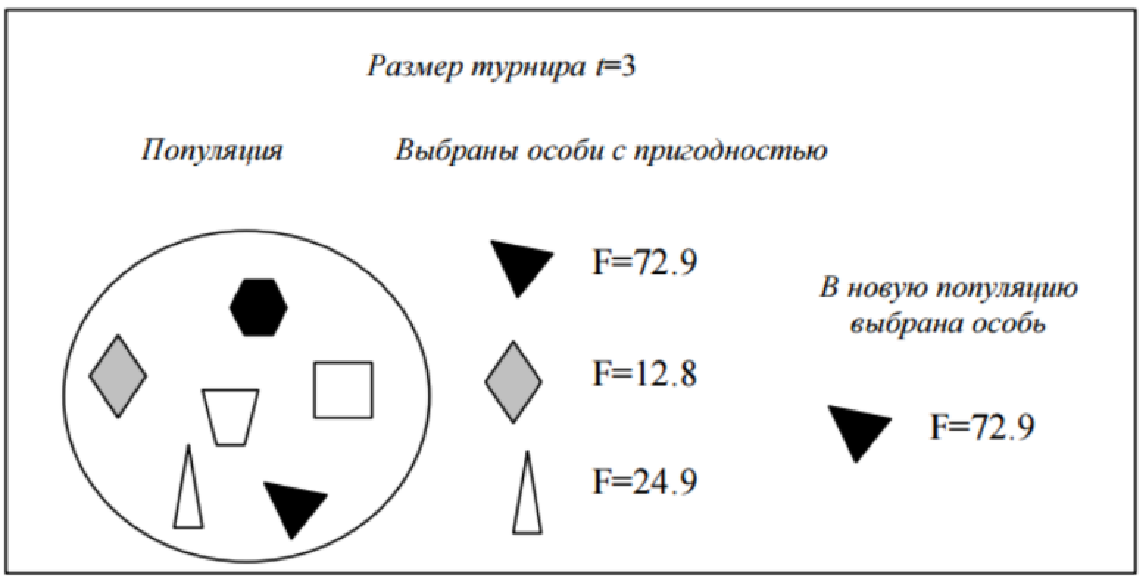
Рисунок 3.1
Другие способы отбора можно получить на основе модификации вышеприведенных. Так, например, в рулеточном отборе можно изменить формулу для вероятности попадания особи в новую популяцию.
Оператор рекомбинации применяют сразу же после оператора отбора родителей для получения новых особей-потомков. Смысл рекомбинации заключается в том, что созданные потомки должны наследовать генную информацию от обоих родителей. Различают дискретную рекомбинацию и кроссинговер.
Дискретная рекомбинация (Discrete recombination) в основном применяется к хромосомам с вещественными генами. Основными способами дискретной рекомбинации являются собственно дискретная рекомбинация, промежуточная, линейная и расширенно линейная рекомбинации. Дискретная рекомбинация соответствует обмену генами между особями.
Промежуточная рекомбинация (Intermediate recombination) применима только к вещественным переменным, но не к бинарным. В данном методе предварительно определяется числовой интервал значений генов потомков, который должен содержать значения генов родителей. Потомки создаются по следующему правилу:
Потомок=Родитель1+𝛼∗(Родитель2−Родитель1),
где множитель α – случайное число на отрезке:
[−𝑑;1+𝑑],𝑑≥0.
При промежуточной рекомбинации возникают значения генов, отличные от значения генов особей-родителей. Это приводит к возникновению новых особей, пригодность которых может быть лучше, чем пригодность родителей. В литературе такой оператор рекомбинации иногда называется дифференциальным скрещиванием.
Был проведён анализ генетических алгоритмов. Для обеспечения решения задач по этой теме было рассмотрино множестао аспектов. Первое, мы выяснили теоритическую строну генетических алгоритмов, так же мы узнали основные понятия, выделили основные операторы.
Мы выяснили, что задачи оптимизации можно решить при помощи генетических алгоритмов, потому что они являются лучшим решением оптимизации.
Разработка данного программного обеспечения направлена студентов что бы помочь им в изучение материала по дисциплине «генетические алгоритмы».
1. Генетические алгоритмы и моделирование биологической эволюции [Электронный ресурс]. – Режим доступа: http://lc.kubagro.ru/aidos/aidos04/1.3.6.htm
2. Стецюра Г.Г. Эволюционные методы в задачах управления, выбора, оптимизации / Стецюра Г.Г. – М. : ФИЗМАТЛИТ, 2006. – 320 с.
3. Панченко Т.В. Генетические алгоритмы: учебно-методическое пособие / Панченко Т.В. – Астрахань : Издательский дом «Астраханский университет», 2007. – 83 с.
4. Генетические алгоритмы [Электронный ресурс]. – Режим доступа: http://mathmod.asu.edu.ru/images/File/ebooks/GAfinal.pdf
5. Рутковская Д.В. Нейронные сети, генетические алгоритмы и нечеткие системы [пер. с польск. И. Д. Рудинского] / Д.В. Рутковская, М.Н. Пилиньский, И.Д. Рутковский – М. : Горячая линия – Телеком, 2006. – 452 с.
6. Емельянов В.В. Теория и практика эволюционного моделирования / Емельянов В.В. – М. : Физматлит, 2003. – 424 с.
7. Курейчик В.М. Поисковая адаптация: теория и практика / Курейчик В.М. – М. : Физматлит, 2006. – 320 с.
8. Задача о ранце – Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Задача_о_ранце
9. Левитин А.В. Алгоритмы. Введение в разработку и анализ / Левитин А.В. – М. : Вильямс, 2007 – С. 456-458
10. Гладков Л.А. Генетические алгоритмы: Учебное пособие / Гладков Л.А – М. : Физматлит, 2009. – 384 с.
11. Скобцов Ю.А. Основы эволюционных вычислений / Скобцов Ю.А. – Донецк : ДонНТУ, 2008. – 326 с.
12. Гладков Л.А. Биоинспирированные методы в оптимизации / Гладков Л.А. – М. : Физматлит, 2009. – 384 с.