Faculty of Computer Science and Technology
Department of Artificial Intelligence and Systems Analysis
Specialty "Software of intelligent systems"
Development and design of a software training module
Scientific adviser: Doctor of Physics and Mathematics, prof. Minenko Alexander Stepanovich
Since genetic and evolutionary optimization algorithms are random search algorithms and are used mainly where it is difficult or impossible to formulate the problem in a form suitable for faster local optimization algorithms (for example, for gradient algorithms, where, in addition, “instantaneous” calculating the gradient of a function represented as a neural network using the back propagation algorithm), or if the task is to optimize an undifferentiable function or a multiextra problem global optimization, their use is very relevant, and to understand the principle of the genetic algorithm, you need to understand how it works and what sequence of processes it includes, which makes the development of the promising module “Genetic Algorithms” an actual software product.
Creating a training module will help students in the study of lecture material by dividing the training material into small theoretical blocks with subsequent testing on the completed training block. Also, the developed software product will allow the teacher to track students' material covered with the ability to view test results for each academic unit, and the administration module will allow you to easily change the content of educational units if necessary.
The developed software module is highly specialized, so it is intended more for students, universities who study the discipline of “genetic algorithms”, and in addition to lecture classes, uses the developed module.
This development is relevant, since no analogues to this software have been identified, which makes this development promising in the future.
Learning using computer technology is considered as a learning method that does not limit the learner and student in time or space, but limits the direct contact. However, the majority of students are usually inert and need constant “pushing”. Many scientists and developers of training programs work on the “pushing” problem, realizing that the most effective is an integrated approach that includes all the components of this process: teacher – training program – student.
The work of the GA is an iterative process, which continues until the generations cease to differ significantly from each other, or a predetermined number of generations or a predetermined time passes. For each generation, selection, crossover (crossing) and mutation are implemented.
Step 1: an initial population of N individuals with random traits is generated.
Step 2 (struggle for existence): the absolute fitness of each individual of the population to environmental conditions f (i) and the total fitness of the individuals of the population, which characterizes the fitness of the entire population, are calculated. Then, with proportional selection for each individual, its relative contribution to the total fitness of the population Ps (i) is calculated, i.e. the ratio of its absolute fitness f (i) to the total fitness of all individuals in the population.
Since the number of offspring of an individual is proportional to its fitness, it is natural to assume that if this is the amount of information:
- positively, this individual survives and gives offspring, the number of which is proportional to this amount of information;
- is equal to zero, then the individual survives to mature age, but does not give offspring (its number is zero);
- less than zero, then the individual dies before reaching adulthood.
Thus, it is possible to draw a fundamental conclusion, even having a worldview sound, that natural selection is the process of generating and accumulating information about the survival and reproduction of genera in a number of generations of a population as a system.
Step 3: start the generational cycle.
Step 4: Beginning of the cycle of formation of a new generation.
Step 5 (selection): a proportional selection of individuals that can participate in procreation is carried out. Only those individuals of the population are selected for which the amount of information in the phenotype and genotype about the survival and reproduction of the genus is positive, and the probability of choice is proportional to this amount of information.
Step 6 (crossover): individuals selected for procreation in the previous step with a given probability Pc are crossed or crossover (recombination).
Step 7 (mutation): mutation operators are executed. Moreover, traits of descendants with probability Pm randomly change to others. I note that the use of the random mutation mechanism makes genetic algorithms related to such a well-known simulation method as the Monte Carlo method.
Step 8 (struggle for existence): the fitness of the descendants is evaluated (using the same algorithm as in step 2).
Step 9: it is checked whether all the selected individuals gave birth. If not, then the transition to step 5 takes place and the formation of a new generation continues, otherwise the transition to the next step 10.
Step 10: there is a generational change according to the following algorithm:
- descendants are placed in a new generation;
- the most adapted individuals from the old generation are transferred to the new one, and for each of them it is possible no more than a specified number of times;
Step 11: the condition for stopping the genetic algorithm is checked. The exit from the genetic algorithm occurs either when new generations cease to be significantly different from the previous ones, that is, as they say, “the algorithm converges”, or when a predetermined number of generations or a given algorithm running time has passed (so that there is no “loop” and dynamic freezing when a solution cannot be found at a given time).
Let's introduce the basic concepts used in genetic algorithms.
Vector is an ordered set of numbers called components of a vector. Since the vector can be represented as a string of its coordinates, then in the future the concepts of the vector and the string are considered identical.
A Boolean vector is a vector whose components take values from two elemental (Boolean) sets, for example, {0, 1} or {−1, 1}.
Hamming distance - used for Boolean vectors and is equal to the number of components that differ in both vectors.
Hamming space is the space of Boolean vectors, with Hamming distance (metric) entered on it. In the case of Boolean vectors of dimension n, the space under consideration is the set of vertices of an n-dimensional hypercube with a hamming metric. The distance between two vertices is determined by the length of the shortest path connecting them, measured along the edges.
A chromosome is a vector (or string) of any numbers. If this vector is represented by a binary string of zeros and ones, for example, 1010011, then it is obtained either using binary coding or the Gray code.
Gene - position (bit) in the chromosome.
Individual (genetic code, individual) - a set of chromosomes (solution to the problem). Usually an individual consists of one chromosome, therefore in the future the individual and the chromosome are identical concepts.
Distance - the hemming distance between binary chromosomes.
Crossover ´ (crossover, crossing) - an operation in which two chromosomes exchange their parts. For example, 1100 & 1010 → 1110 & 1000.
Mutation - a random change in one or more positions in the chromosome. For example, 1010011 → 1010001.
Inversion - a change in the sequence of bits in the chromosome or in its fragment. For example, 1100 → 0011.
A population is a collection of individuals.
Fitness (fitness) - a criterion or function whose extremum should be found.
Locus - the position of the gene in the chromosome.
Allele - a collection of consecutive genes.
Epistasis is the effect of a gene on an individual’s fitness, depending on the value of the gene present elsewhere. A gene is considered epistatic when its presence suppresses the influence of the gene at another locus. Epistatic genes are sometimes called inhibitory because of their effect on other genes. Suppression of gene expression by a non-allelic gene is called hypostasis, and the suppressed gene itself is called hypostatic.
The main operators of the genetic algorithm can be divided into 3 groups:
- parent selection operators (selection operators);
- crossing (recombination) operators;
- mutation.
Panmixia is the easiest selection operator. In accordance with it, a random integer on the segment [1; n], where n is the number of individuals in the population.
We will consider these numbers as the numbers of individuals that will take part in the crossing. With this choice, some of the members of the population will not participate in the reproduction process, since they form a pair with themselves. Some members of the population will take part in the reproduction process repeatedly with various individuals of the population.
Despite its simplicity, this approach is universal for solving various classes of problems. However, it is quite critical for the population size, since the efficiency of the algorithm that implements this approach decreases with increasing population size.
Inbreeding is a method in which the first parent is randomly selected and the second parent is the member of the population closest to the first. Here “nearest” can be understood, for example, in the sense of the minimum Hamming distance (for binary strings) or the Euclidean distance between two real vectors. Hamming distance is equal to the number of different loci (bits) in the binary string.
Inbreeding and outbreeding have different effects on the behavior of the genetic algorithm.
So, inbreeding can be characterized by the property of concentration of the search in local nodes, which actually leads to the division of the population into separate local groups around areas of terrain that are suspicious of extremum.
Outbreeding is aimed at preventing the algorithm from converging to already found solutions, forcing the algorithm to view new, unexplored areas.
Inbreeding and outbreeding can be genotypic (when the difference in the values of the objective function for the corresponding individuals is taken) and phenotypic (the Hamming distance is taken as the distance)
During tournament selection, t individuals are randomly selected from a population containing N individuals, and the best individual is recorded in an intermediate array (see Fig. 3.1). This operation is repeated N times. The individuals in the resulting intermediate array are then used for crossbreeding (also randomly). The size of a group of rows selected for a tournament is often 2. In this case, we are talking about a binary (pair) tournament. In general, t is called the size of the tournament.
The advantage of this method is that it does not require additional calculations.
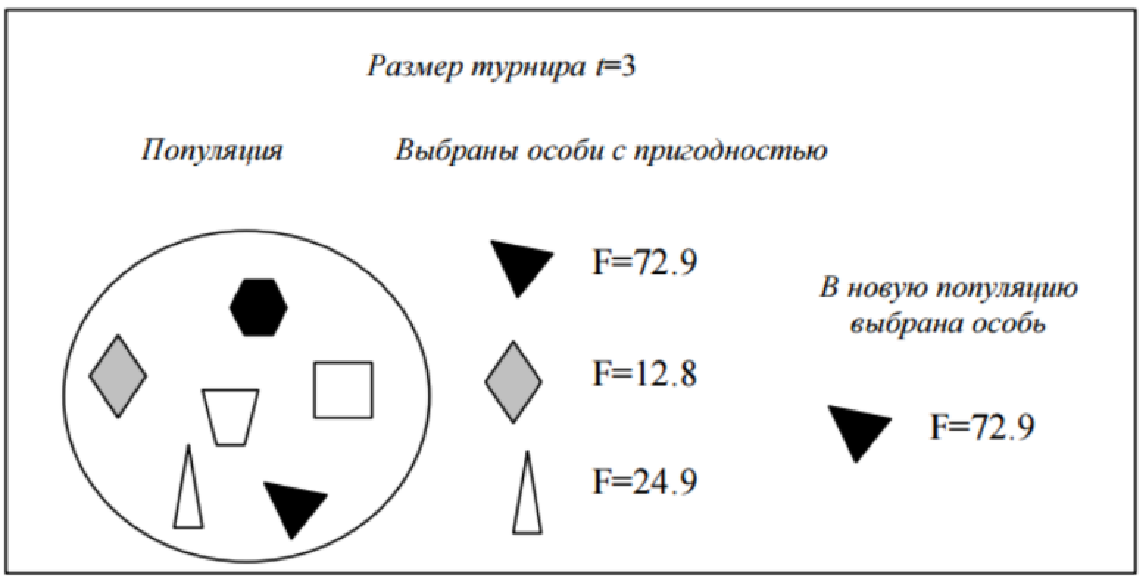
Figure 3.1
Other selection methods can be obtained based on a modification of the above. So, for example, in roulette selection you can change the formula for the probability of an individual entering a new population.
The recombination operator is used immediately after the parent selection operator to obtain new offspring. The meaning of recombination is that the created descendants must inherit the gene information from both parents. There are discrete recombination and crossing over.
Discrete recombination is mainly applied to chromosomes with material genes. The main methods of discrete recombination are actually discrete recombination, intermediate, linear and expanded linear recombination. Discrete recombination corresponds to the exchange of genes between individuals.
Intermediate recombination is applicable only to real variables, but not to binary ones. In this method, the numerical range of the gene values of the descendants, which should contain the values of the genes of the parents, is preliminarily determined. Descendants are created by the following rule:
Descendant = Parent1 + 𝛼 ∗ (Parent2 − Parent1),
where the factor α is a random number on the segment:
[−𝑑; 1 + 𝑑], 𝑑≥0.
With intermediate recombination, gene values differ from the genes of the parent individuals. This leads to the emergence of new individuals whose suitability may be better than the suitability of parents. In the literature, such a recombination operator is sometimes called differential crossover.
An analysis of genetic algorithms was carried out. To ensure the solution of problems on this topic, many aspects were considered. First, we found out the theoretical side of genetic algorithms, we also learned the basic concepts, identified the main operators.
We found that optimization problems can be solved using genetic algorithms, because they are the best optimization solution.
The development of this software is aimed at students to help them study material on the subject of «genetic algorithms».
1. Генетические алгоритмы и моделирование биологической эволюции [Электронный ресурс]. – Режим доступа: http://lc.kubagro.ru/aidos/aidos04/1.3.6.htm
2. Стецюра Г.Г. Эволюционные методы в задачах управления, выбора, оптимизации / Стецюра Г.Г. – М. : ФИЗМАТЛИТ, 2006. – 320 с.
3. Панченко Т.В. Генетические алгоритмы: учебно-методическое пособие / Панченко Т.В. – Астрахань : Издательский дом «Астраханский университет», 2007. – 83 с.
4. Генетические алгоритмы [Электронный ресурс]. – Режим доступа: http://mathmod.asu.edu.ru/images/File/ebooks/GAfinal.pdf
5. Рутковская Д.В. Нейронные сети, генетические алгоритмы и нечеткие системы [пер. с польск. И. Д. Рудинского] / Д.В. Рутковская, М.Н. Пилиньский, И.Д. Рутковский – М. : Горячая линия – Телеком, 2006. – 452 с.
6. Емельянов В.В. Теория и практика эволюционного моделирования / Емельянов В.В. – М. : Физматлит, 2003. – 424 с.
7. Курейчик В.М. Поисковая адаптация: теория и практика / Курейчик В.М. – М. : Физматлит, 2006. – 320 с.
8. Задача о ранце – Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Задача_о_ранце
9. Левитин А.В. Алгоритмы. Введение в разработку и анализ / Левитин А.В. – М. : Вильямс, 2007 – С. 456-458
10. Гладков Л.А. Генетические алгоритмы: Учебное пособие / Гладков Л.А – М. : Физматлит, 2009. – 384 с.
11. Скобцов Ю.А. Основы эволюционных вычислений / Скобцов Ю.А. – Донецк : ДонНТУ, 2008. – 326 с.
12. Гладков Л.А. Биоинспирированные методы в оптимизации / Гладков Л.А. – М. : Физматлит, 2009. – 384 с.