Факультет комп'ютерних наук і технологій
Кафедра штучного інтелекту і системного аналізу
Спеціальність « Програмне забезпечення інтелектуальних систем »
Розробка та проектування програмного навчального модуля
Науковий керівник: д.ф.-м.н., проф. Міненко Олександр Степанович
Так як генетичні та еволюційні алгоритми оптимізації є алгоритмами випадково-спрямованого пошуку і застосовуються в основному там, де складно або неможливо сформулювати завдання у вигляді, придатному для більш швидких алгоритмів локальної оптимізації (наприклад, для градієнтних алгоритмів, де можливо, до того ж, «миттєве» обчислення градієнта представленої у вигляді нейронної мережі функції за допомогою алгоритму зворотного поширення помилки), або якщо стоїть завдання оптимізації недиференційованої функції або завдання многоекстр емальной глобальної оптимізації, то їх використання є дуже актуальним, а для розуміння принципу роботи генетичного алгоритму необхідно розуміти як він працює і яку послідовність процесів в себе включає, що робить розробку обіцяє модуля «Генетичні алгоритми» актуальним програмним продуктом.
Створення навчального модуля допоможе студентам у вивченні лекційного матеріалу шляхом поділу навчального матеріалу на не великі теоретичні блоки з наступним тестуванням з пройденого навчального блоку. Так само розроблений програмний продукт дозволить викладачеві відстежувати пройдений матеріал студентів з можливістю перегляду результатів тестування з кожного навчального блоку, а модуль адміністрації дозволить легко змінити зміст навчальних блоків при необхідності.
Розроблюваний програмний модуль є вузькоспеціалізованим, так призначений в більшій мірі для студентів, університетів, які вивчають дисципліну «генетичні алгоритми», і на додаток до лекційних занять користується розробляються модулем.
Дана розробка є актуальною, так як аналогів даного програмного не було виявлено, що робить дану розробку перспективної в майбутньому.
Навчання з використанням комп'ютерних технологій розглядається як спосіб навчання, що не обмежує навчає і навчається в часі або просторі, але обмежує безпосередні контакти. Однак основна маса учнів, як правило, інертна і потребує постійного «підштовхуванні». Над проблемою «підштовхування» працюють багато вчених і розробники навчальних програм, розуміючи, що найефективніший - це комплексний підхід, в який включаються всі складові цього процесу: викладач - навчальна програма - навчається.
Робота ГА являє собою ітераційний процес, який триває до тих пір, поки покоління не перестануть істотно відрізнятися один від одного, або не пройде заданий кількість поколінь або заданий час. Для кожного покоління реалізуються відбір, кросовер (схрещування) і мутація.
Крок 1: генерується початкова популяція, що складається з N особин з випадковими наборами ознак.
Крок 2 (боротьба за існування): обчислюється абсолютна пристосованість кожної особини популяції до умов середовища f (i) і сумарна пристосованість особин популяції, що характеризує пристосованість всієї популяції. Потім при пропорційному відборі для кожної особини обчислюється її відносний внесок у сумарну пристосованість популяції Ps (i), тобто ставлення її абсолютної пристосованості f (i) до сумарної пристосованості всіх особин популяції.
Оскільки кількість потомства особини пропорційно її пристосованості, то природно вважати, що якщо ця кількість інформації:
- позитивно, то дана особина виживає і дає потомство, чисельність якого пропорційна цій кількості інформації;
- дорівнює нулю, то особина доживає до статевозрілого віку, але потомства не дає (його чисельність дорівнює нулю);
- менше нуля, то особина гине до досягнення статевозрілого віку.
Таким чином, можна зробити фундаментальний висновок, що має навіть світоглядне звучання, про те, що природний відбір є процес генерації та накопичення інформації про виживання і продовження роду в ряді поколінь популяції, як системи.
Крок 3: початок циклу зміни поколінь.
Крок 4: початок циклу формування нового покоління.
Крок 5 (відбір): здійснюється пропорційний відбір особин, які можуть брати участь в продовженні роду. Відбираються тільки ті особини популяції, у яких кількість інформації в фенотипі і генотипі про виживання і продовження роду позитивно, причому ймовірність вибору пропорційна цій кількості інформації.
Крок 6 (кросовер): відібрані для продовження роду на попередньому кроці особини із заданою вірогідністю Pc піддаються схрещуванню або кросоверу (рекомбінації).
Крок 7 (мутація): виконуються оператори мутації. При цьому ознаки нащадків з імовірністю Pm випадковим чином змінюються на інші. Зазначу, що використання механізму випадкових мутацій ріднить генетичні алгоритми з таким широко відомим методом імітаційного моделювання, як метод Монте-Карло.
Крок 8 (боротьба за існування): оцінюється пристосованість нащадків (за тим же алгоритмом, що і на кроці 2).
Крок 9: перевіряється, чи всі відібрані особи дали потомство.Еслі немає, то відбувається перехід на крок 5 і триває формування нового покоління, інакше - перехід на наступний крок 10.
Шаг 10: происходит смена поколений по следующему алгоритму:
- потомки помещаются в новое поколение;
- найбільш пристосовані особини зі старого покоління переносяться в нове, причому для кожної з них це можливо не більше заданої кількості разів;
Крок 11: перевіряється виконання умови зупинки генетичного алгоритму. Вихід з генетичного алгоритму відбувається або тоді, коли нові покоління перестають істотно відрізнятися від попередніх, тобто, як кажуть, «алгоритм сходиться», або, коли пройдено задану кількість поколінь або заданий час роботи алгоритму (щоб не було «зациклення» і динамічного зависання в разі, коли рішення не може бути знайдено в заданий час).
Введемо основні поняття, що застосовуються в генетичних алгоритмах.
Вектор - упорядкований набір чисел, які називаються компонентами вектора. Так як вектор можна представити у вигляді рядка його координат, то в подальшому поняття вектора і рядки вважаються ідентичними.
Логічний вектор - вектор, компоненти якого приймають значення з двох елементного (булева) безлічі, наприклад, {0, 1} або {-1, 1}.
Хеммінгово відстань - використовується для булевих векторів і дорівнює числу розрізняються в обох векторах компонент.
Хеммінгово простір - простір булевих векторів, з введенням на ньому відстанню (метрикою) Хемминга. У разі булевих векторів розмірності n розглядається простір являє собою безліч вершин n-мірного гіперкуба з хеммінговой метрикою. Відстань між двома вершинами визначається довжиною найкоротшого з'єднує їх шляху, виміряної уздовж ребер.
Хромосома – вектор (або рядок) з будь-яких чисел. Якщо цей вектор представлений бінарної рядком з нулів і одиниць, наприклад, 1010011, то він отриманий або з використанням двійкового кодування, або коду Грея.
Ген – позиція (біт) в хромосомі.
Індивідуум (генетичний код, особина) – набір хромосом (варіант вирішення завдання). Зазвичай особина складається з однієї хромосоми, тому в подальшому особина і хромосома ідентичні поняття.
Відстань – хеммінгово відстань між бінарними хромосомами.
Кроссинговер (кросовер, схрещування) – операція, при якій дві хромосоми обмінюються своїми частинами. Наприклад, 1100 & 1010 → 1110 & 1000.
Мутація – випадкове зміна однієї або декількох позицій у хромосомі. наприклад, 1010011 → 1010001.
Інверсія – зміна порядку проходження бітів в хромосомі або в її фрагменті. Наприклад, 1100 → 0011.
Популяція – сукупність індивідуумів.
Придатність (пристосованість) – критерій або функція, екстремум якої слід знайти.
Локус – позиція гена в хромосомі.
Аллель – сукупність поспіль генів.
Епістаз – вплив гена на придатність індивідуума в залежності від значення гена, присутнього в іншому місці. Ген вважають Епістатичний, коли його присутність пригнічує вплив гена в іншому локусі. Епістатичні гени через їх впливу на інші гени іноді називають інгібують. Придушення прояви гена неалельні йому геном називається гіпостазов, а сам придушений ген - гіпостатична.
Основні оператори генетичного алгоритму можна розбити на 3 групи:
- оператори вибору батьків (оператори відбору);
- оператори схрещування (рекомбінації);
- мутація.
Панміксія – найпростіший оператор відбору. Відповідно до нього кожному члену популяції зіставляється випадкове ціле число на відрізку [1; n], де n – кількість особин в популяції.
Будемо розглядати ці числа як номери особин, які візьмуть участь в схрещуванні. При такому виборі якісь із членів популяції не будуть брати участь в процесі розмноження, так як утворюють пару самі з собою. Якісь члени популяції візьмуть участь в процесі відтворення неодноразово з різними особинами популяції.
Незважаючи на простоту, такий підхід універсальний для вирішення різних класів задач. Однак він досить критичний до чисельності популяції, оскільки ефективність алгоритму, що реалізує такий підхід, знижується зі зростанням чисельності популяції.
Інбридинг є такий метод, коли перший батько вибирається випадковим чином, а другим батьком є член популяції найближчий до першого. Тут «найближчий» можна розуміти, наприклад, в сенсі мінімальної відстані Хеммінга (для бінарних рядків) або евклидова відстані між двома речовими векторами. Відстань Хеммінга дорівнює числу розрізняються локусів (розрядів) в бінарній рядку.
Інбридинг і аутбридинг по-різному впливають на поведінку генетичного алгоритму.
Так, інбридинг можна охарактеризувати властивістю концентрації пошуку в локальних вузлах, що фактично призводить до розбиття популяції на окремі локальні групи навколо підозрілих на екстремум ділянок ландшафту.
Аутбридинг ж спрямований на попередження збіжності алгоритму до вже знайденим рішенням, змушуючи алгоритм переглядати нові, недосліджені області.
Інбридинг і аутбридинг буває генотипного (коли в якості відстані береться різниця значень цільової функції для відповідних особин) і фенотипних (як відстані береться відстань Хеммінга)
При турнірному відборі (tournament selection) з популяції, що містить N особин, вибираються випадковим чином t особин, і найкраща з них особина записується в проміжний масив (див. зоб. 3.1). Ця операція повторюється N раз. Особи в отриманому проміжному масиві потім використовуються для схрещування (також випадковим чином). Розмір групи рядків, що відбираються для турніру, часто дорівнює 2. У цьому випадку говорять про довічним (парному) турнірі. Взагалі ж t називають чисельністю турніру.
Перевагою даного способу є те, що він не вимагає додаткових обчислень.
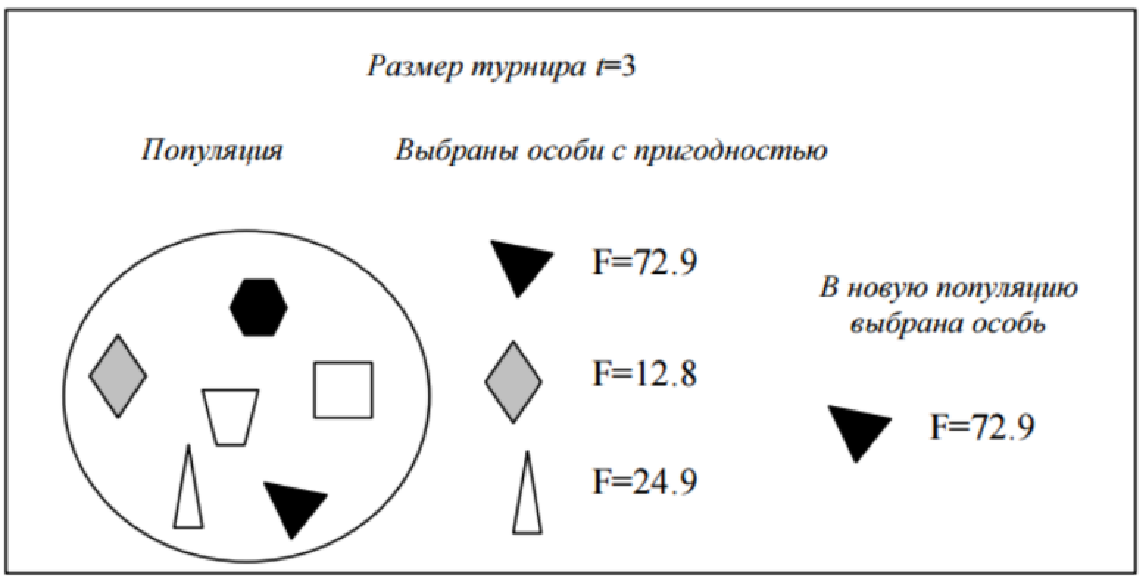
Зображення 3.1
Інші способи відбору можна отримати на основі модифікації вищенаведених. Так, наприклад, в рулеточним відборі можна змінити формулу для ймовірності потрапляння особини в нову популяцію.
Оператор рекомбінації застосовують відразу ж після оператора відбору батьків для отримання нових особин-нащадків. Сенс рекомбінації полягає в тому, що створені нащадки повинні наслідувати генну інформацію від обох батьків. Розрізняють дискретну рекомбінацію і кросинговер.
Дискретна рекомбінація (Discrete recombination) в основному застосовується до хромосом з речовими генами. Основними способами дискретної рекомбінації є власне дискретна рекомбінація, проміжна, лінійна і розширено лінійна рекомбінації. Дискретна рекомбінація відповідає обміну генами між особинами.
Проміжна рекомбінація (Intermediate recombination) може бути застосована тільки до речових змінним, але не до бінарним. В даному методі попередньо визначається числовий інтервал значень генів нащадків, який повинен містити значення генів батьків. Нащадки створюються за наступним правилом:
Нащадок =Батько1+𝛼∗(Батько2−Батько1),
де множник α – випадкове число на відрізку:
[−𝑑;1+𝑑],𝑑≥0.
При проміжної рекомбінації виникають значення генів, відмінні від значення генів особин-батьків. Це призводить до виникнення нових особин, придатність яких може бути краще, ніж придатність батьків. У літературі такий оператор рекомбінації іноді називається диференціальним схрещуванням.
Був проведений аналіз генетичних алгоритмів. Для забезпечення вирішення завдань по цій темі було рассмотріно множестао аспектів. Перше, ми з'ясували теоритических строну генетичних алгоритмів, так само ми дізналися основні поняття, виділили основні оператори.Ми з'ясували, що завдання оптимізації можна вирішити за допомогою генетичних алгоритмів, тому що вони є кращим рішенням оптимізації.
Розробка даного програмного забезпечення спрямована студентів що б допомогти їм у вивчення матеріалу з дисципліни «генетичні алгоритми».
1. Генетические алгоритмы и моделирование биологической эволюции [Электронный ресурс]. – Режим доступа: http://lc.kubagro.ru/aidos/aidos04/1.3.6.htm
2. Стецюра Г.Г. Эволюционные методы в задачах управления, выбора, оптимизации / Стецюра Г.Г. – М. : ФИЗМАТЛИТ, 2006. – 320 с.
3. Панченко Т.В. Генетические алгоритмы: учебно-методическое пособие / Панченко Т.В. – Астрахань : Издательский дом «Астраханский университет», 2007. – 83 с.
4. Генетические алгоритмы [Электронный ресурс]. – Режим доступа: http://mathmod.asu.edu.ru/images/File/ebooks/GAfinal.pdf
5. Рутковская Д.В. Нейронные сети, генетические алгоритмы и нечеткие системы [пер. с польск. И. Д. Рудинского] / Д.В. Рутковская, М.Н. Пилиньский, И.Д. Рутковский – М. : Горячая линия – Телеком, 2006. – 452 с.
6. Емельянов В.В. Теория и практика эволюционного моделирования / Емельянов В.В. – М. : Физматлит, 2003. – 424 с.
7. Курейчик В.М. Поисковая адаптация: теория и практика / Курейчик В.М. – М. : Физматлит, 2006. – 320 с.
8. Задача о ранце – Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Задача_о_ранце
9. Левитин А.В. Алгоритмы. Введение в разработку и анализ / Левитин А.В. – М. : Вильямс, 2007 – С. 456-458
10. Гладков Л.А. Генетические алгоритмы: Учебное пособие / Гладков Л.А – М. : Физматлит, 2009. – 384 с.
11. Скобцов Ю.А. Основы эволюционных вычислений / Скобцов Ю.А. – Донецк : ДонНТУ, 2008. – 326 с.
12. Гладков Л.А. Биоинспирированные методы в оптимизации / Гладков Л.А. – М. : Физматлит, 2009. – 384 с.