Реферат по темі випускної роботи
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: червень 2021 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Зміст
- Введення
- 1.Методи геометричного моделювання
- 2.Комплекс універсальних аналітичних методів моделювання складних геометричних об'єктів та їх перетворень
- 2.1 Метод гладкого сполучення кривих і площин
- 2.2 Метод повороту геометричного об'єкта навколо осі, що проходить через задану точку простору
- Висновок
- Список джерел
Введення
Математичне моделювання фізико–механічних процесів та інженерних споруд часто пов'язано з необхідністю створення геометричних моделей. З їх допомогою можна визначити образ існуючого або проектованого об'єкта, провести відповідний постановці завдання чисельний експеримент і здійснити необхідні корекції. Геометричною моделлю в широкому сенсі називається сукупність формального опису досліджуваного об'єкта і відповідного йому візуального образу, представленого в просторах різної розмірності. Формальним описом в зв'язку з розвитком сучасних методів комп'ютерного моделювання в першу чергу є чисельне моделювання геометричних об'єктів навколишнього світу. При цьому їх різноманіття створюється з використанням базових геометричних елементів: точки, лінії і поверхні.
1. Методи геометричного моделювання
Геометричне моделювання в даний час розвивається за двома напрямками. Перший напрямок – чисельні методи в задачах САПР і комп'ютерної графіки. Сучасні етапи впровадження САПР характеризуються переходом від плоского моделювання до об'ємного. Точність моделі геометричного об'єкта забезпечується точністю здійснення перетворення базового примітиву. Для плоского моделювання, основними об'єктами моделювання є відрізки, дуги, полілінії і криві, в тому числі криві Безьє, сплайни, раціональні криві. Базові перетворення на їх основі – продовження, обрізка і з'єднання. В об'ємному моделюванні основні об'єкти – це замкнуті контури. При цьому використовуються поверхні руху, лінійчатих, поверхні Безьє, Кунса. Головні операції – булеві: об'єднання, доповнення, перетин, а також перетворення повороту і трансляції. Існує поняття базової поверхні, з якої в процесі моделювання здійснюють ту чи іншу перетворення. В результаті засобами САПР проектований об'єкт чисельно конструюється з геометричних тіл, званих графічними примітивами, які можуть бути трансформовані тими чи іншими програмними засобами. Аналітичного представлення нових форм, одержуваних такими перетвореннями, не існує.
Другий напрямок геометричного моделювання представлено роботами, де геометричні об'єкти задаються в аналітичному вигляді. Виділено понад 500 аналітично заданих поверхонь 38 класів, які можуть бути використані при вирішенні різних завдань науки і техніки. Аналітичні методи представлення геометричних об'єктів мають високий ступінь точності. Можуть бути різні форми опису об'єктів і їх перетворень – векторні, операторні, тензорні і інші форми, що дозволяє задавати кожну точку геометричного об'єкта і виконувати довільні перетворення в аналітичному вигляді. В основі класифікації аналітичних поверхонь істотну роль мають ті способи, в результаті яких ці поверхні виходять. Існує великий клас поверхонь, які отримані перетворенням обертання плоскої кривої навколо осі Oz. Ще один великий клас поверхонь виходить перетворенням перенесення кривої деякого напряму, так що її одна точка ковзає по інший кривої. Більш складні перетворення утворюють класи гвинтових, спіралеподібних і інших поверхонь. Поповнення відомого набору аналітичних поверхонь новими і розширення їх класів становить інтерес для розвитку методів геометричного моделювання та їх додатків. Важливою складовою досліджень в цьому напрямку може бути розширення різноманіття поверхонь і створення нових аналітичних форм шляхом різних перетворень: доповнень, поворотів, перетинів і інших. Використання аналітичних методів може бути початковим етапом проектування. Це дозволяє після верифікації відповідних геометричних моделей транслювати їх в графічні пакети, які підтримують геометричні масштаби для отримання проектної документації.
Існують алгоритми гладкого сполучення кривих і площин при розробці системи геометричного моделювання машинобудівних деталей на основі чисельних методів. Для їх застосування потрібно описати об'єкти сполучення в формі поверхні або кривої Безьє, або сплайновой поверхні відповідно, як розглянуто в роботах. Ступінь гладкості сполучення залежить від кількості контрольних точок, що в свою чергу збільшує алгебраїчну ступінь кривих, і ускладнює чисельні розрахунки. Більш широко дані методи моделювання використовуються для поверхневого моделювання складних об'ємних форм.
Сполучення поверхонь в комп'ютерній геометрії здійснюється для операції округлення ребер. Для цього будують нові грані, які різним чином поєднують тіла, які стикуються в скругляются ребрах. В основі цих методів лежать геометричні алгоритми з використанням поверхонь заокруглення постійного радіусу і поверхонь, що представляють собою сліди від кочення сфери, частин циліндричних поверхонь і поверхонь тора. У разі якщо потрібно побудувати поверхню змінного радіуса, то опорна дуга поверхні сполучення представляється у вигляді раціональної кривої Безьє. Також розглядаються і гладкі поверхні, що сполучаються – еліптичні, параболічні і гіперболічні, які виходять варіюванням функції ваги середньої точки, заданої раціональної кривої Безьє. При цьому не досліджувалося питання кривизни і ступеня гладкості такого сполучення. Виникає від залучення чисельних методів похибка, в описаних методах гладкого сполучення при визначенні точок дотику вимагає додаткових досліджень.
Дослідженню перетворення центрального проектування присвячений розділ геометрії – проективна геометрія, яка розвинулася і виділилася в окрему гілку знань в перші десятиліття 19 століття в зв'язку з потребою розвитку теорії зображень в перспективі. Геометр Жан Віктор Понселе один з перших виділив особливі властивості геометричних фігур, названі ним проектними. Проективна геометрія становить геометрію класу проективних перетворень і вдає із себе систему теорем, які стверджують низовина властивостей фігур в цьому класі. Ідея класифікації різних галузей геометрії відповідно до класів перетворень належить Феліксу Клейну.
Метод створення перспективного зображення широко застосовується в комп'ютерній графіці при створенні реалістичного зображення. В основі методу в популярних і конкуруючих між собою пакетах OpenGL і DirectX лежить побудова так званої проекційної матриці і її застосування для створення проектованого зображення. Перетворення здійснюється з використанням однорідних координат з переходом на заключній стадії до декартових для визначення положення координати тривимірної вершини на двовимірному екрані монітора.
Формування проекційної матриці для створення необхідної ілюзії здійснюється за допомогою чотирьох параметрів: кут огляду в радіанах – fovy, співвідношення сторін – aspect, відстань до ближньої площини відсікання (n), відстань до далекої площині відсікання – f.
В даних методах об'єкт проектування задається організованим програмним чином масивом координат. При використанні аналітичних форм виникає обов'язкова необхідність в переході до таких масивів перед здійсненням перетворення проектування. Використовуються різні методи, зокрема, тріангуляції, для можливості виконання процедур відповідно до аксіоматикою проективної геометрії. Серйозні обчислювальні труднощі виникають в тих випадках, коли проектується об'єкт, площина проектування або центр проектування змінюють своє положення в просторі довільним чином. Всі алгоритми отримання проектних зображень пов'язані з необхідністю переходів від декартових координат до однорідних і потім вимагають виконання зворотного переходу.
2. Комплекс універсальних аналітичних методів моделювання складних геометричних об'єктів та їх перетворень
При цьому для завдання геометричних об'єктів і їх перетворень використовується векторне подання, не залежне від вибраного координатного базису, на всій стадії вирішення. Таке уявлення можна назвати інваріантним. Поняття інваріантності базується на концепції Ф.Клейна, як властивості деякого класу математичних об'єктів, що залишаються незмінними при перетвореннях, і на принципі інваріантності геометричних понять Г.Ф.Лаптева, як зв'язку геометричних понять з даної фігурою, повністю визначаються фігурою і не залежать від способу її завдання. Формальним інструментом для побудови математичних моделей є вектори і кватерніони, як об'єкти, що дозволяють здійснювати алгебраїчні перетворення, зберігаючи принцип інваріантності геометричних понять. Основними компонентами рішення є алгебраїчний підхід до вирішення векторних рівнянь, включаючи диференціальні і аналітичний метод побудови кривих і поверхонь.
2.1 Метод гладкого сполучення кривих і площин
Різноманіття форм аналітичних поверхонь дозволяє вирішувати різні завдання геометричного моделювання в графічному дизайні, архітектурно–будівельній сфері, судно– і авіабудуванні, машинобудуванні. Розширенню можливості аналітичних методів завдання поверхонь в задачах формоутворення може сприяти гладке сполучення площин. Гладке сполучення з використанням примітивів в якості інструменту згладжування або заокруглення постійного / змінного радіуса ефективно застосовується в CAD–системах.
Розглянемо аналітичний метод гладкого сполучення площин на прикладі сполучення двох пересічних площин, довільно орієнтованих в просторі, що дозволяє отримати поверхню сполучення в аналітичному вигляді з заданим порядком гладкості.
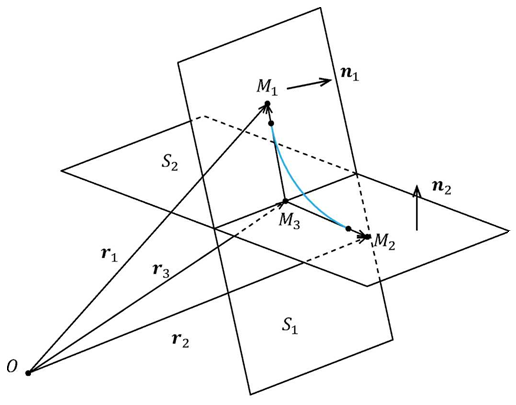
На першому етапі рішення задачі введемо в розгляд дві площини S1 і S2, які задані своїми нормальними одиничними векторами і радіус–векторами r1, r2 фіксованих точок (рис.2.1).
Аналітична запис лінії перетину площин може бути представлена системою векторних рівнянь
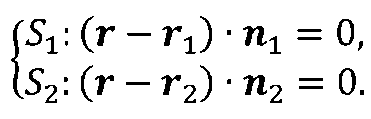
(рис 2.1)
Перший крок процедури вирішення поставленого завдання полягає в отриманні лінії перетину площин в параметричної формі
Рівняння лінії перетину площин L шукається в наступній параметричної формі
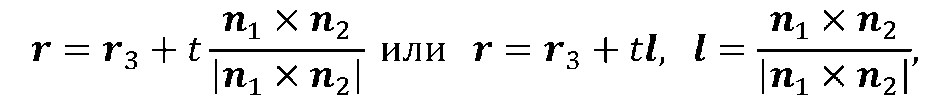
(рис 2.2) де r3 – радіус–вектор точки на прямій L, l – одиничний вектор цієї прямої.
На наступному кроці знаходиться положення такої точки М3, яка лежить на перетині прямої L з перпендикулярно розташованої до неї прямий, що у площині St і проходить через точку Мг. Положення цієї точки може бути знайдено шляхом вирішення системи наступних рівнянь
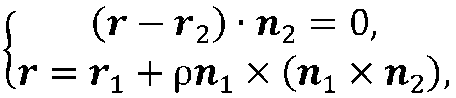
(рис 2.3) де р – параметр системи.
Перше рівняння задає площину S2, а друге рівняння задає пряму в параметричної формі, що проходить через точку М1; що лежить в площині S1 і перпендикулярну L.
Підставами в систему (2.3) радіус–вектор точки М3. Виключаючи з цієї системи вектор г3, знаходимо значення параметра р
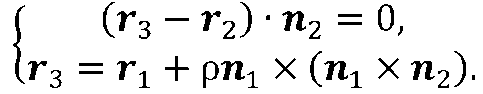
Крім із цієї системи вектор r3, знаходимо значення параметра р
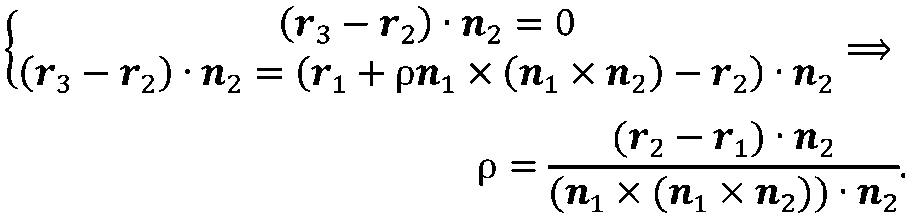
Підставляючи знайдене значення параметра р у другу рівність системи (2.3), знаходимо положення точки М3
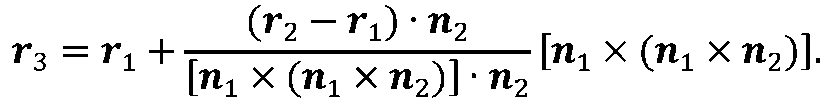
(рис 2.4)
З використанням тотожності
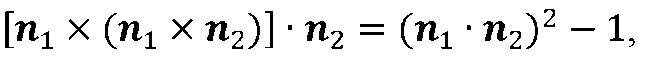
Яке випливає з правила обчислення подвійного векторного твори, формула (2.4) перетвориться до виду
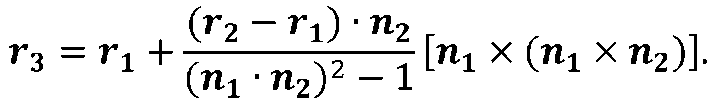
Підстановка отриманого значення г3 в формулу (2.2) дає рівняння лінії перетину площин St і S2 в інваріантної параметричної формі
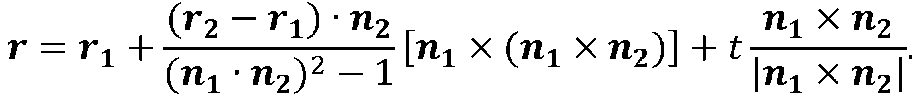
(рис 2.5)
При цьому знаменник звертається в нуль, коли площини паралельні.
Подальше рішення задачі гладкого сполучення площин полягає в знаходженні променів L1і L2. Промені Lt і L2 виходять з точки М3, лежать в площинах S1 і S2 і перпендикулярні до прямої L.
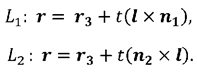
Далі на променях Lt і L2 вибираються точки на відстанях dt і d2 від лінії перетину площин. Їхнє становище при цьому визначається рівностями
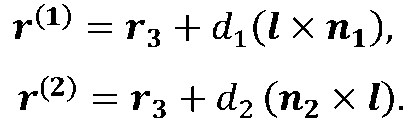
Гладке сполучення променів Lt і L2 здійснюється за допомогою векторного полінома п'ятого ступеня
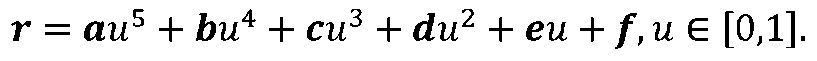
(рис 2.6)
Ступінь полінома вибирається з умов забезпечення гладкого сполучення променів L1 і L2, при якому виконуються наступні крайові умови:
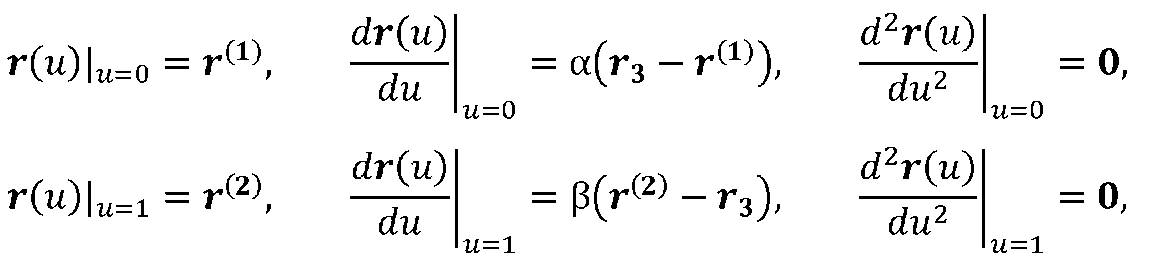
Підстановка векторного полінома (2.6) в крайові умови призводить до наступної системи лінійних рівнянь з векторними невідомими
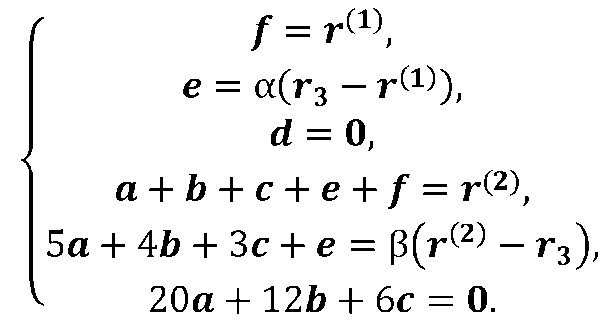
Ця система зводиться до матричного рівняння відносно трьох невідомих векторів а, b, с.
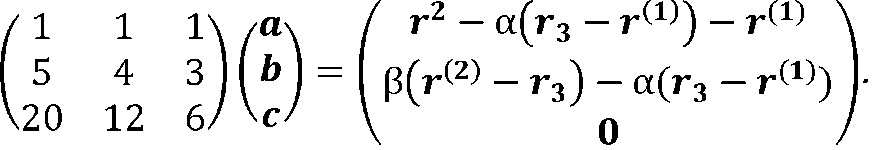
Рішення цієї системи в інваріантної формі записується рівністю
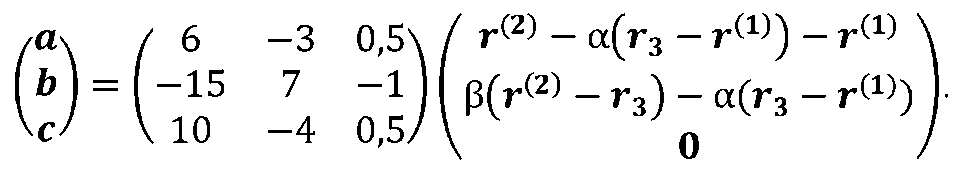
Звідки
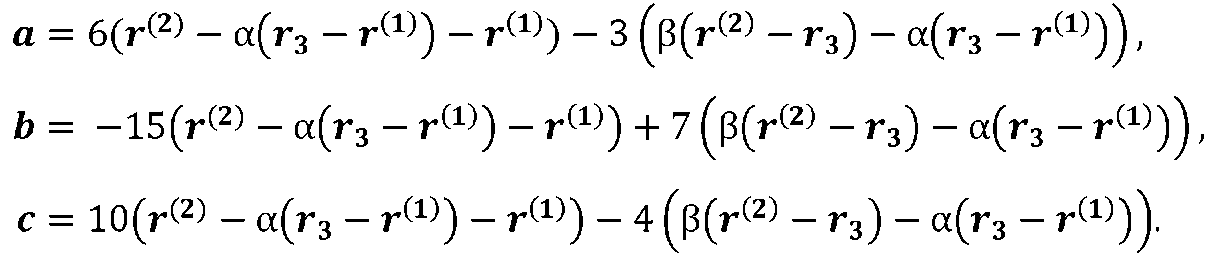
Звичайно, поверхня, яка реалізує гладке сполучення площин S1 і S2, знаходиться, як поверхня перенесення з котра утворює у вигляді полінома п'ятого ступеня (2.6) і спрямовуючим вектором l.
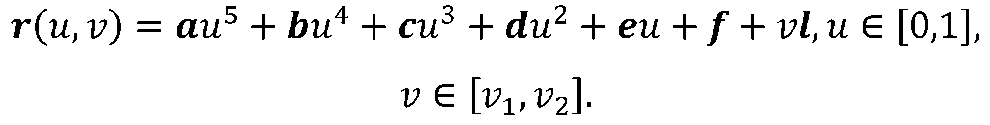
(рис 2.7)
Як приклад розглядається сполучення, виконане в системі комп'ютерної алгебри Mathcad, двох площин (рис.2.2).
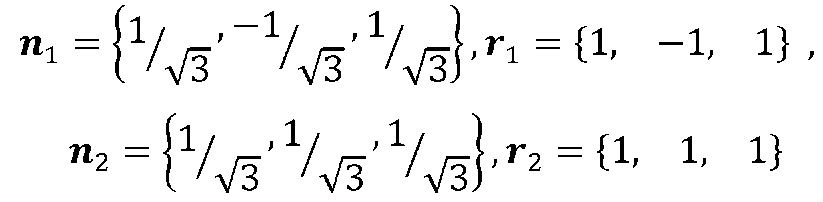
при значеннях параметрів
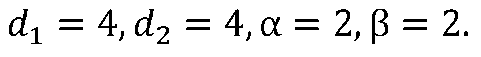
За рівняння утворює кривої
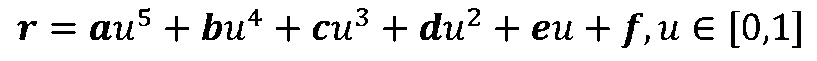
визначається кривизна на інтервалі сполучення по формулі
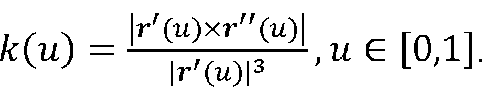
Базова лінія сполучення двох площин
2.2 Метод гладкого сполучення кривих і площин
Поворот або обертання тривимірного евклідового простору разом з паралельним переносом утворюють так звану підгрупу руху групи афінних перетворень. Математичні алгоритми перетворення повороту затребувані при вирішенні різних завдань динаміки твердого тіла, робототехніки, мультиплікації, твердотільного моделювання. Для вирішення завдань використовуються різні алгоритми. Так, поворот навколо осі довільним чином орієнтованої в просторі традиційно вирішується шляхом послідовного виконання операцій паралельного перенесення і повороту навколо координатних осей.
Розглянемо узагальнений метод повороту навколо осі з одиничним направляють вектором I, що проходить через задану точку простору Мг. При такому перетворенні всі крапки осі залишаються нерухомими, а інші точки повертаються в площинах перпендикулярних цієї осі на один і той же кут д.
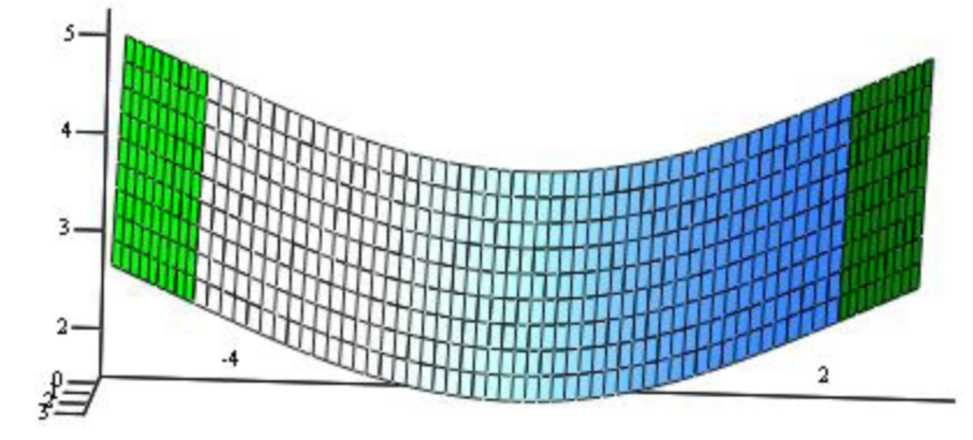
Поверхность гладкого сполучення двох площин
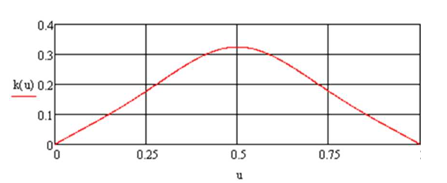
Графік зміни кривизни утворює кривої поверхні гладкого сполучення, побудований в системі комп'ютерної алгебри Mathcad
З урахуванням рівності
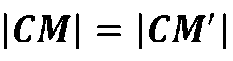
маємо
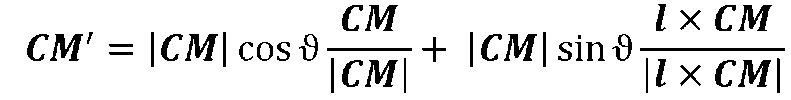
або
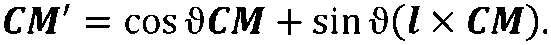
З геометричних міркувань знаходимо, що
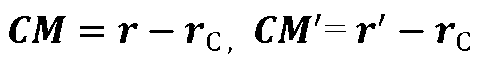
При цьому
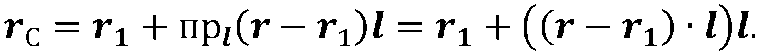
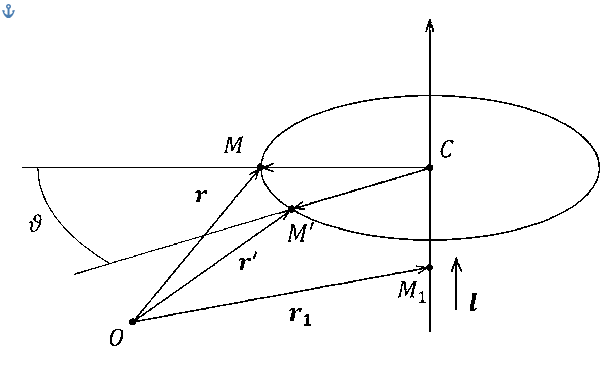
Схема повороту точки М евклідового простору навколо довільної осі, з одиничним направляють вектором I, що проходить черезточку Мг
Як випливає з графіка зміни кривизни утворює кривої (рис. 2.3) при даних значеннях коригувальних параметрів аїр зміна кривизни утворює кривої відбувається симетрично. Шляхом варіювання цих параметрів зміна кривизни може бути реалізовано за різними законами з урахуванням необхідних цілей моделювання.
Висновок
За результатами аналізу існуючих методів геометричного моделювання встановлено, що при математичному моделюванні складних геометричних об'єктів і їх перетворень використовуються два основні підходи – чисельні методи в задачах САПР, комп'ютерної графіки та аналітичне геометричне моделювання. Засобами САПР проектований об'єкт чисельно конструюється з геометричних тіл, званих графічними примітивами, які можуть бути трансформовані тими чи іншими програмними засобами. Точність моделі геометричного об'єкта забезпечується точністю здійснення поточечного перетворення базового примітиву. Аналітичні ж методи мають високий ступінь точності результатів моделювання, так як аналітично задається кожна точка геометричного об'єкта та перетворення виконуються синхронно.
Існують алгоритми гладкого сполучення кривих і площин при розробці системи геометричного моделювання машинобудівних деталей методами САПР на базі використання чисельних методів. Ступінь гладкості сполучення залежить від кількості контрольних точок, що збільшує і алгебраїчну ступінь кривих сполучення і ускладнює чисельні розрахунки.
Операцію заокруглення ребер здійснюють методами комп'ютерної геометрії, в основі яких лежить сполучення в аналітичній формі з використанням поверхонь постійного радіуса
Основним застосуванням методів створення перспективних зображень є рішення задач комп'ютерної візуалізації. Теоретичні основи відповідних методів закладені в проективної геометрії. Основними інструментами при моделюванні побудови центральної проекції є проектні матриці в однорідних координатах з використанням глобальних і локальних систем координат. Об'єкт проектування задається поточечно – числовим масивом його координат. Розташування площині проектування є строго фронтальній.
Поряд з розглянутими, можливий інший підхід до математичного моделювання представлених вище перетворень, коли об'єкти моделювання задані в аналітичній формі, а все перетворення виконуються в аналітичному вигляді незалежно від вибору системи координат.
Огляд існуючих методів опису повороту твердого тіла, як найбільш широко використовуваного перетворення, свідчить про велику різноманітність підходів до вирішення завдання. Об'єднуючим є використання в різних формах подання матриці повороту навколо осі, що проходить через початок координат. Поворот навколо осі, що проходить через довільну точку простору здійснюється шляхом композиції перетворення повороту щодо координатних осей і перетворення трансляції. При цьому обов'язковою умовою є введення рухомою і нерухомою системи відліку.
Ефективним засобом опису сферичного руху твердого тіла є використання кватерніонів параметризації, яка в останні роки знаходить все більше застосування в задачах управління рухом, робототехніки та комп'ютерної анімації. При цьому популярність набуває метод сферичної лінійної інтерполяції кватернионов. Методи нелінійної інтерполяції кватернионов, що дозволяють в більш широкому діапазоні задавати кінематичні закони сферичного руху в науковій літературі відсутні. Це призводить до необхідності отримання незалежних від вибору системи координат і зручних для реалізації в пакетах комп'ютерної алгебри алгоритмів опису повороту твердого тіла щодо осі довільного положення.
Результат огляду дозволяє зробити висновок про доцільність створення універсальних математичних методів для аналітичного опису складних геометричних об'єктів і їх перетворень в основі яких лежить виконання вимог незалежності від вибору системи координат і сумісності з існуючими аналітичними уявленнями об'єктів
Саме такі методи дозволять здійснити комп'ютерне моделювання перетворень складних геометричних об'єктів у пакетах комп'ютерної алгебри.
Список джерел
- Казановіч Я.Б. Сегментація зображень за допомогою динамічних нейронних мереж / Я.Б. Казановіч. // Наукова сесія МІФІ–2008. Х Всеросійська науково–технічна конференція
Нейроінформатика–2008
: Лекції по нейроінформатіке – Частина 2. – М .: МІФІ, 2008. – C. 37–97. - Запряжи, С.А. Програмна оболонка для пошуку примітивів на зображенні / С.А.Запрягаев, А.І. Сорокін. // Вісник ВДУ, Серія Системний аналіз та інформаційні технології – №2 – 2008. – С. 37–47.
- Введення в контурний аналіз: додатки до обробки зображень і сигналів / Под ред. Я.А.Фурмана. – М .: ФИЗМАТЛИТ, 2003. – 592 с.
- Виноградов, А.Н. Виділення і розпізнавання локальних об'єктів на аерокосмічних знімках / [Виноградов А.Н. та ін.]. // авіакосмічного приладобудування – № 9 – 2007. – С.39–45.
- Хайкін, С. Нейронні мережі: повний курс / С. Хайкін., [Пер. з англ.]. – 2–е вид. – М .: Вільямс, 2006. – 1104 с.
- Єрмоленко, А.В. Застосування перетворення Фур'є для перетворення об'єктів при нейромережевому аналізі образів / А.В. Єрмоленко. // Збірник праць конференції
Інтегровані моделі і м'які обчислення в штучному інтелекті
– М .: Изд–во МГТУ ім. Н.е. Баумана, 2009. – C. 39–75. - Бочаров, Д.М. Методи перетворення 2D–фотографій приміщення в 3D–модель / Д.М. Бочаров, Р.А. Сорокін // Сучасні інформаційні системи и технології: матеріали Другої міжнародної науково–практичної конференции (Суми, 21–24 травня 2013 року.) / Сумський державний університет. – Суми, – 2013. – С. 150–151.
- Бочаров, Д.М. Попередня обробка 2D–зображень при 3D–реконструкції / Д.М. Бочаров, Р.А. Сорокін // Штучний інтелект. Інтелектуальні системи ШІ–2013: матеріали міжнародної науково–технічної конференції (сел. Кацивелі АР Крим, 23 – 27 сентября 2013 року) / Донецький національний технічний університет. Донецьк, – 2013.– С.70–72.
- Бочаров, Д.М. Фільтрація і сегментація зображень для задач 3D–реконструкції / Д.М. Бочаров, Р.А. Сорокін // Інформаційні управляючі системи та комп'ютерний моніторинг: матеріали V міжнародної науково–технічної конференції студентів, аспірантів і молодих вчених (Донецьк, 22 – 23 квітень 2014 роки) / Донецький національний технічний університет. – Донецьк, – 2014. – С. 398–404.
- Кудряшов, А.П. Реконструкція тривимірних сцен міської обстановки / А.П. Кудряшов // Інформаційні технології. – № 7. – 2009. – С. 63–68.
- Сорокін, Р.А. Виділення геометричних фігур на фотоизображении / Р.А. Сорокін, Д.М. Бочаров // Інноваційні перспективи Донбасу: матеріали міжнародної науково–практичної конференції (Донецьк, 20–22 травня 2015 року) / Донецький національний технічний університет. – Донецьк, – 2015. – С. 86–90.
- Казановіч Я.Б. Сегментація зображень за допомогою динамічних нейронних мереж / Я.Б. Казановіч. // Наукова сесія МІФІ–2008. Х Всеросійська науково–технічна конференція
