Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

От первобытных ритуалов до современных высокобюджетных компьютерных проектов, игры были одной из важнейших частей нашего бытия. Они развлекают, оказывают терапевтическое воздействие и обучают людей. В данной работе мы будем рассматривать специфический вид игр, которые зародился в 40–х годах двадцатого столетия. Но широкое распространение получил в 70–х – 80–х годах прошлого века. Речь идет о компьютерных играх.

По википедии «Компьютерная игрa – компьютерная программа, служащая для организации игрового процесса (геймплея), связи с партнёрами по игре, или сама выступающая в качестве партнёра»[1]. Благодаря техническому прогрессу разработка программного обеспечения в сфере развлечений стал общедоступным и простым

Одним из важных элементов игры является игровая механика, то–есть набор правил и способов которые и реализуют игровой процесс. Взаимодействие с неигровыми персонажами является одной из таких механик. Разработка механик и правил по которым эти персонажи существуют в игре является очень трудоемким процессом. Но не менее важным, так как взаимодействие с персонажами в ролевых или аркадных играх является основным костяком самой игры.

1. Цель и задачи исследования, планируемые результаты

Целью моей дипломной работы является разработка и программная реализация модели поведения неигровых персонажей.

Задачей моего исследования это разработать программную реализацию поведения неигрового персонажа. Также разработать игровой движок для дальнейшего использования.

Одним из способов эмоционально привязать человека к выдуманному игровому миру, это создать иллюзию жизни и наполненности. За это ответственные персонажи компьютерной игры, а в частности их поведение и реакция на действия игрока. Они могут быть, как и, дружелюбными их называют неигровыми персонажами (NPC от англ. Non–player character), так и враждебными к игроку боты (от англ. Bot) и мобы (от англ. Mob).

По википедии «Неигровой персонаж – персонаж в играх, который не находится под контролем игрока.»[2]

Планируемые результаты моей работы – это разработка алгоритма принятия решений неигровым персонажем и реализация основной части механики игры на pygame. В дальнейшем планирую развивать игру и при переходе на более лучший ПК перенос на более лучший ПК.

2. Обзор исследований и разработок

2.1 Обзор международных источников

Исследования по модели поведения были начаты еще в 40–х годах прошлого века из книги Норберта Вайнера «Кибернетика, или управление и коммуникации между человеком и машиной».[3] В книге «Транспортные средства: эксперименты в синтетической психологии»[4] Валентино Брайтенберг описывает серию мысленных экспериментов, в которых «транспортные средства» с простой внутренней структурой ведут себя неожиданно сложным образом.

Брайтенберг приводит это как доказательство «закона восходящего анализа и нисходящего изобретения», имея в виду, что гораздо труднее попытаться угадать внутреннюю структуру, просто наблюдая за поведением, чем создать структуру, которая задает поведение.

В книге «Шампандар А.Дж. Искусственный интеллект в компьютерных играх: как обучить виртуальные персонажи реагировать на внешние воздействия»[5] показано, как ввести в компьютерную игру синтетические игровые персонажи с реалистичными формами поведения, сосредоточиваясь на отдельных аниматах (автономных созданиях с искусственным телом), находящихся в виртуальном мире. В «Artificial Intelligence for Games»[6] Ян Миллингтон привносит обширный профессиональный опыт в решение проблемы повышения качества ИИ в играх.Он описывает множество примеров из реальных игр и исследует лежащие в их основе идеи с помощью подробных тематических исследований. Он идет дальше, чтобы представить множество техник, которые сегодня мало используются разработчиками.

2.2 Обзор национальных источников

В работе «Разработка модели поведения персонажей»[7] рассматривается стратегии поведения, применяемые для решения задачи, используются для описания выбора пути передвижения объектов. В статье «Конечно–автоматная модель управления интеллектуальных агентов в обучающих играх»[8] рассматривается применение конечно–автоматной модели для моделирования поведения интеллектуальных агентов. Проводится обоснование выбора конечно–автоматной модели поведения. Описывается реализация программной платформы для моделирования поведения.

В статье «Интеллектуальные системы в компьютерных играх. Перспективы развития искусственного интеллекта в игровой индустрии»[9] рассматриваются особенности технической реализации искусственного интеллекта в играх, основные методы создания интеллектуальных систем, предлагаются варианты их улучшения, а также описываются перспективы развития данной области информационных технологий.

2.3 Обзор локальных источников

В работе магистра Буга К.В. «Изучение методов построения игрового искусственного интеллекта и разработка информационной технологии для ее реализации в пошаговых стратегиях»[10] рассмотрены методы построения универсального искусственного интеллекта и способы передвижения. Исследование и разработка игрового ИИ на основе генетического алгоритма проводил Жудин А.Ю. в своей работе «Исследование и разработка игрового искусственного интеллекта с помощью генетического алгоритма для коллекционной карточной игры Dual choice»[11]. Также разработкой игрового движка занимался Шкимба А.А. в работе «Средства разработки игрового движка для игры в жанре стратегия»[12].

3. Краткое описание работы

Поиск пути – термин в информатике и искусственном интеллекте, который означает определение компьютерной программой наилучшего, оптимального маршрута между двумя точками.

Поиск пути в контексте компьютерных игр касается пути, на котором движущийся объект ищет путь вокруг препятствий. Наиболее часто задача поиска пути возникает в стратегиях реального времени, в которых игрок даёт задание игровым юнитам (единицам) двигаться через игровой уровень, который содержит препятствия. Кроме стратегий, задача поиска пути, так или иначе, в той или иной мере встречается в большинстве современных игровых жанров. Так как игры становятся всё сложнее, то поиск пути также эволюционирует и развивается вместе с ними.

3.1 Алгоритм A звезда

A* пошагово просматривает все пути, ведущие от начальной вершины в конечную, пока не найдёт минимальный. Как и все информированные алгоритмы поиска, он просматривает сначала те маршруты, которые «кажутся» ведущими к цели. От жадного алгоритма, который тоже является алгоритмом поиска по первому лучшему совпадению, его отличает то, что при выборе вершины он учитывает, помимо прочего, весь пройденный до неё путь. Составляющая g(x) – это стоимость пути от начальной вершины, а не от предыдущей, как в жадном алгоритме.

В начале работы просматриваются узлы, смежные с начальным; выбирается тот из них, который имеет минимальное значение f(x), после чего этот узел раскрывается. На каждом этапе алгоритм оперирует с множеством путей из начальной точки до всех ещё не раскрытых (листовых) вершин графа – множеством частных решений, – которое размещается в очереди с приоритетом. Приоритет пути определяется по значению f(x) = g(x) + h(x).

Алгоритм продолжает свою работу до тех пор, пока значение f(x) целевой вершины не окажется меньшим, чем любое значение в очереди, либо пока всё дерево не будет просмотрено. Из множества решений выбирается решение с наименьшей стоимостью. Чем меньше эвристика h(x), тем больше приоритет, поэтому для реализации очереди можно использовать сортирующие деревья. Как и алгоритм поиска в ширину, A* является полным в том смысле, что он всегда находит решение, если таковое существует.

Если эвристическая функция h допустима, то есть никогда не переоценивает действительную минимальную стоимость достижения цели, то A* сам является допустимым (или оптимальным), также при условии, что мы не отсекаем пройденные вершины. Если же мы это делаем, то для оптимальности алгоритма требуется, чтобы h(x) была ещё и монотонной, или преемственной эвристикой. A* и допустим, и обходит при этом минимальное количество вершин, благодаря тому, что он работает с «оптимистичной» оценкой пути через вершину. Оптимистичной в том смысле, что, если он пойдёт через эту вершину, у алгоритма «есть шанс», что реальная стоимость результата будет равна этой оценке, но никак не меньше. Но, поскольку A* является информированным алгоритмом, такое равенство может быть вполне возможным.

Когда A* завершает поиск, он, согласно определению, нашёл путь, истинная стоимость которого меньше, чем оценка стоимости любого пути через любой открытый узел. Но поскольку эти оценки являются оптимистичными, соответствующие узлы можно без сомнений отбросить. Иначе говоря, A* никогда не упустит возможности минимизировать длину пути, и потому является допустимым.

Предположим теперь, что некий алгоритм B вернул в качестве результата путь, длина которого больше оценки стоимости пути через некоторую вершину. На основании эвристической информации, для алгоритма B нельзя исключить возможность, что этот путь имел и меньшую реальную длину, чем результат. Соответственно, пока алгоритм B просмотрел меньше вершин, чем A*, он не будет допустимым. Итак, A* проходит наименьшее количество вершин графа среди допустимых алгоритмов, использующих такую же точную (или менее точную) эвристику. На рисунке 1 показан пример работы алгоритма.

Алгоритм А*

Рисунок 1 – Пример работы алгоритма А*анимация (25 кадров, цикл повторений: бесконечно, размер: 45 кб)

3.2 Волновой алгоритм

Алгоритм работает на дискретном рабочем поле (ДРП), представляющем собой ограниченную замкнутой линией фигуру, не обязательно прямоугольную, разбитую на прямоугольные ячейки, в частном случае – квадратные. Множество всех ячеек ДРП разбивается на подмножества: «проходимые» (свободные), т. е при поиске пути их можно проходить, «непроходимые» (препятствия), путь через эту ячейку запрещён, стартовая ячейка (источник) и финишная (приемник). Назначение стартовой и финишной ячеек условно, достаточно – указание пары ячеек, между которыми нужно найти кратчайший путь.

Алгоритм предназначен для поиска кратчайшего пути от стартовой ячейки к конечной ячейке, если это возможно, либо, при отсутствии пути, выдать сообщение о непроходимости. Работа алгоритма включает в себя три этапа: инициализацию, распространение волны и восстановление пути. Во время инициализации строится образ множества ячеек обрабатываемого поля, каждой ячейке приписываются атрибуты проходимости/непроходимости, запоминаются стартовая и финишная ячейки.

Далее, от стартовой ячейки порождается шаг в соседнюю ячейку, при этом проверяется, проходима ли она, и не принадлежит ли ранее меченной в пути ячейке. Соседние ячейки принято классифицировать двояко: в смысле окрестности Мура и окрестности фон Неймана, отличающийся тем, что в окрестности фон Неймана соседними ячейками считаются только 4 ячейки по вертикали и горизонтали, в окрестности Мура – все 8 ячеек, включая диагональные.

При выполнении условий проходимости и непринадлежности её к ранее помеченным в пути ячейкам, в атрибут ячейки записывается число, равное количеству шагов от стартовой ячейки, от стартовой ячейки на первом шаге это будет 1. Каждая ячейка, меченная числом шагов от стартовой ячейки, становится стартовой и из неё порождаются очередные шаги в соседние ячейки. Очевидно, что при таком переборе будет найден путь от начальной ячейки к конечной, либо очередной шаг из любой порождённой в пути ячейки будет невозможен.

Восстановление кратчайшего пути происходит в обратном направлении: при выборе ячейки от финишной ячейки к стартовой на каждом шаге выбирается ячейка, имеющая атрибут расстояния от стартовой на единицу меньше текущей ячейки. Очевидно, что таким образом находится кратчайший путь между парой заданных ячеек. Трасс с минимальной числовой длиной пути, как при поиске пути в окрестностях Мура, так и фон Неймана может существовать несколько. Выбор окончательного пути в приложениях диктуется другими соображениями, находящимися вне этого алгоритма. Например, при трассировке печатных плат – минимумом линейной длины проложенного проводника.

На рисунках 2 – 3 показаны шаги работы волнового алгоритма на графе.

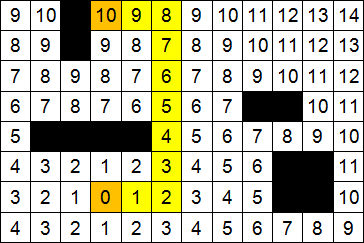
волновой алгоритм

Рисунок 2 – Пример исполььзования алгоритма

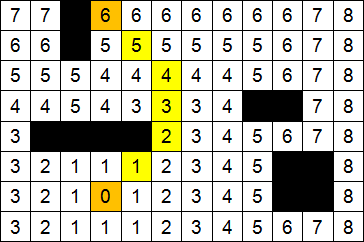
волновой алгоритм

Рисунок 3 – Пример исполььзования алгоритма

3.3 Графический движок

За графику в игровом движке отвечает графический движок. Наилучшее определение понятия графический движок найдено на википедии: Графический движок – это промежуточное программное обеспечение, программный движок, основной задачей которого является визуализация (рендеринг) двухмерной или трёхмерной компьютерной графики [13].

Зачастую графический движок является наиболее сложным компонентом игрового движка, поэтому он вполне претендует на звание главного компонента игрового движка. По этой причине графические движки редко распространяются отдельно сами по себе и часто включаются в какой–либо другой продукт (игровой движок, в частности). Однако подобное правило не относится к свободному программному обеспечению, созданному энтузиастами, которые создают свободные графические движки, которые затем можно подключить как модуль к своему проекту как и остальные компоненты, входящие в игровой движок.

Список источников

  1. Википедия. Компьютерная игра [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Компьютерная_игра
  2. Неигровой персонаж [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Неигровой_персонажа
  3. Wiener, Norbert // Cybernetics, or control and communication in the animal and the machine. Cambridge, Massachusetts: The Technology Press; New York: John Wiley & Sons, Inc.
  4. Braitenberg, Valentino // Vehicles: Experiments in Synthetic Psychology, The MIT Press, Cambridge, MA. 1984г.
  5. Шампандар А.Д. Искусственный интеллект в компьютерных играх: как обучить виртуальные персонажи реагировать на внешние воздействия. : Пер. с англ. – М. : ООО «И.Д. Вильямс», 2007. – 768 с
  6. Millington, Ian Artificial intelligence for games / Ian Millington, John Funge. – 2nd ed. – 895 с.
  7. Анохин А.О. Конечно–автоматная модель управления интеллектуальных агентов в обучающих играх / А.О. Анохин, А.В. Катаев // ИТНОУ: Информационные технологии в науке, образовании и управлении, № 4 (14), 2019. – с. 75–80.
  8. Буковшин В.А. Интеллектуальные системы в компьютерных играх. Перспективы развития искусственного интеллекта в игровой индустрии / В.А. Буковшин, С.Г. Воскобойников // Современные материалы, техника и технологии, №3 (11), 2017. – ст 21–36
  9. Буга К.В. «Изучение методов построения игрового искусственного интеллекта и разработка информационной технологии для ее реализации в пошаговых стратегиях»[Электронный ресурс]. – Режим доступа: http://masters.donntu.ru/2013/fknt/buga/bio/index.htm
  10. Жудин А.Ю. «Исследование и разработка игрового искусственного интеллекта с помощью генетического алгоритма для коллекционной карточной игры Dual choice» http://masters.donntu.ru/2017/fknt/zhudin/
  11. Шкимба А.А. «Средства разработки игрового движка для игры в жанре стратегия» http://masters.donntu.ru/2014/fknt/shkimba/index.htm
  12. Википедия. Графический движок [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/...