Реферат по теме выпускной работы
На момент написания данного реферата магистерская диссертация не завершена. Планируемая дата завершения работы — лето 2021 г.
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1. Обзор международных источников
- 3.2. Обзор национальных источников
- 3.3. Обзор локальных источников
- 4. Введение в теорию МКЭ
- Выводы
- Список источников
Введение
Для анализа прочностных характеристик конструкций проводят инженерные расчёты с применением аналитических и численных методов. Аналитические методы требуют от инженера высокого уровня математической подготовки и, как правило, позволяют решать задачи только для тел с относительно простой геометрической формой. Эффективность численных методов в то же время не ограничивается ни сложностью геометрии тел, ни способами приложения сил.
Метод конечных элементов (МКЭ) — один из современных методов численного анализа, который изначально развивался в двух направлениях независимо — в инженерном деле и в математике. Сложные инженерные конструкции заменялись более простыми с использованием стержней в соответствии с методами статики линейных опор. В математике акцент был на решении краевых задач, которые тогда подразумевали вариационный метод. Позднее два подхода слились в один, что имело большое значение для распространения МКЭ. В 1941 г. А. П. Хренников — канадский инженер русского происхождения — впервые применил метод физической дискретизации сплошной среды при решении плоской задачи теории упругости. Это подтолкнуло других исследователей к дальнейшему изучению свойств дискретных структур.
Впервые МКЭ был применён для проведения расчётов инженерных конструкций в 50-х гг. ХХ в., когда задачей было решение проблемы плоского напряжения. Вскоре после этого МКЭ стал самостоятельной областью науки. Его развитие происходило параллельно с развитием компьютерной вычислительной техники, что также способствовало расширению возможностей для исследования и моделирования задач математики, физики и механики.
Быстрое развитие инженерной мысли требовало более точных расчётов, особенно в авиации, где необходимы высокие показатели грузоподъёмности и надёжности при минимальной массе [1][2].
1. Актуальность темы
Надежность и эффективность создаваемых инженерных конструкций в большой степени зависят от возможности прогнозирования их поведения под воздействием различных внешних факторов. Достоверность прогнозирования в свою очередь напрямую коррелирует с точностью применяемых для этого технологий. Уверенность в том, что новая конструкция выдержит предполагаемые нагрузки, и при этом позволяет более рационально расходовать материалы, привносит некие дополнительные функциональные возможности или ещё что-либо, благоприятно сказывается на развитии огромного количества отраслей промышленности.
Одним из самых распространённых методов прогнозирования поведения тел под воздействием внешних факторов сегодня является метод конечных элементов. С его помощью решаются такие задачи, как задача механики деформации твёрдого тела, задачи теории упругости, задачи о распространении тепла, задачи гидрогазодинамики и др. Теории и реализации МКЭ посвящено множество научных работ и литературы. Помимо универсальности его популярность обусловлена непосредственной связью с классическими методами строительной механики и независимостью от геометрической формы исследуемых тел.
Существует множество современных инструментов проектирования конструкций, где МКЭ играет одну из важнейших ролей, например, САПР Catia, SolidWorks, КОМПАС-3D и др.
2. Цель и задачи исследования, планируемые результаты
Цель исследования: поиск возможных путей оптимизации программной реализации метода конечных элементов.
Объект исследования: метод конечных элементов.
Предмет исследования: оптимизация алгоритма метода конечных элементов с применением современных технологий.
Основные задачи исследования:
- Ознакомление с математикой МКЭ.
- Проектирование программной реализации МКЭ.
- Анализ алгоритма МКЭ на предмет потенциальных участков оптимизации.
- Анализ современных методов и технологий, способных оптимизировать операции в обнаруженных участках.
- Программная реализация прототипа оптимизированного алгоритма МКЭ.
В рамках магистерской работы планируется получение следующих научных результатов:
- Список потенциальных участков оптимизации алгоритма МКЭ.
- Рабочий прототип оптимизированного алгоритма МКЭ.
3. Обзор исследований и разработок
В литературе по данной теме считается, что метод конечных элементов заключается в применении методов строительной механики для аппроксимации решения задач механики сплошных сред.
На рисунке 1 видно, что пиковым периодом публикаций на тему МКЭ являются 1980‑е гг. как для русскоязычного, так и для англоязычного общества.
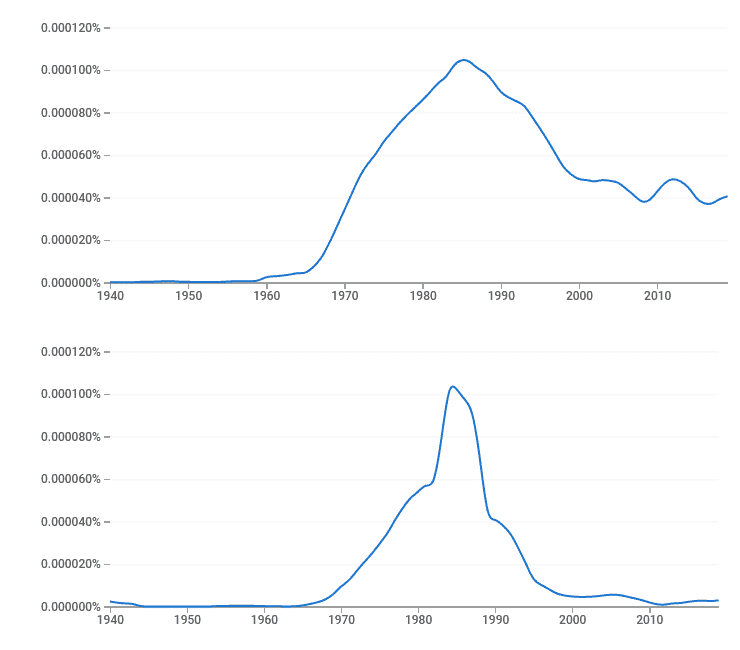
Рисунок 1 — Графики распределения частоты упоминания МКЭ в литературе на английском (сверху) и русском (снизу) языках в период 1940–2019 гг. [3][4]
3.1. Обзор международных источников
Одними из основоположников идей, лежащих у начал МКЭ, считаются канадский инженер русского происхождения Александр Хренников и американский математик немецкого происхождения Рихард Курант. Их работы опубликованы в 1940-х годах [5][6]. В своей более поздней работе Хренников пишет, что один из первых подобий МКЭ был разработан ещё в 1941 г. для решения проблем теории упругости методами расчётов стержневых систем и изначально применялся для расчёта плоских плит, заменяемых сетчатой системой из большого количества соединённых треугольных или прямоугольных ячеек.
Значительный вклад в разработку МКЭ сделал грек Иоаннис Аргирис, преподававший в то время авиаинженерию в Лондоне. Он впервые дал общую матричную формулировку расчета стержневых систем на базе фундаментальных энергетических принципов, определил матрицу податливости, а позже — матрицу жёсткости (как обратную матрице податливости). Работы Аргириса и его сотрудников, опубликованные в период 1954–1960 гг., являются стартовой точкой для матричной формулировки известных численных методов и расчетов конструкций с применением ЭВМ. В его работе Energy Theorems and Structural Analysis
впервые встречается термин конечный элемент
. В ней же осуществлено обобщение основных энергетических принципов, которые использовались для расчёта конструкций [7].
Американский учёный Рэй Уильям Клаф в своей работе The Finite Element Method in Plane Stress Analysis
при решении двумерной задачи теории упругости дробит двумерный континуум на треугольные или четырёхугольные элементы, которые после соединяются в узлах. В ней использована уже известная матричная формулировка, позаимствована идея представления сплошной среды в виде конечного числа элементов. Новизна заключается в том, что в качестве конечных элементов использовались двумерные и трёхмерные конструктивные элементы [8].
В 2016 г. М. Непли добился повышения производительности при интегрировании МКЭ с использованием графических процессоров. На тот момент видеокарта NVIDIA GTX580 обрабатывала в алгоритме оператор Лапласа со скоростью почти 3*10^11 операций с плавающей запятой в секунду с переменными коэффициентами в двух измерениях и свыше 4*10^11 — в трёх, чему посвящена работа Finite Element Integration with Quadrature on the GPU
[9].
В статье A computational framework for G/XFEM material nonlinear analysis
(2017 г.) А. Монтейро с соавторами описывает разработанный фреймворк для нелинейного анализа веществ, созданный с целью преодоления некоторых ограничений МКЭ [10]. Позднее М. Малекан с участниками той же команды опубликовал статью Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach
, где представил объектно-ориентированную реализацию G/XFEM [11].
Работа GPU-warp based finite element matrices generation and assembly using coloring method
(2019 г.) под авторством У. Кирана описывает новые стратегии генерации матриц для МКЭ на основе метода раскраски, а также объясняет извлечённую пользу технологий CUDA [12].
3.2. Обзор национальных источников
В книге Метод конечных элементов в механике разрушения
(1980 г.) Е. Морозов излагает основные понятия метода конечных элементов и способы его реализации в задачах механики разрушения. Автор раскрывает широкий круг вопросов — от методов расчета коэффициентов интенсивности напряжений в плоских и осесимметричных телах при механическом и термическом нагружении пластически деформированных областей и параметров локального разрушения в случае развитой пластической зоны до ряда вычислительных экспериментов, помогающих решению сложных вопросов механического поведения упруго-пластических тел с трещинами. В приложении к книге даны алгоритмы решения основных задач, оформленных в виде программ для ЭВМ на языке ФОРТРАН [13].
В Пластической деформации легких и специальных сплавов
(1982 г.) Н. Корягин рассматривает теоретические и практические вопросы воздействия сил на металлы и сплавы. Раскрыты методы исследования деформированных тел в состоянии напряжения и теплообмена. Изложены условия и принципы формирования механических свойств тел при горячей прокатке. Книга содержит результаты исследований пластических деформаций лёгких и специальных сплавов при различных взаимодействиях тел. Также рассмотрены вопросы сопротивления пластической деформации, механических свойств тел при пластической деформации, методики исследования механических свойств [14].
В 2004 г. Р. Даутов изложил основные способы построения и анализа схем МКЭ в учебном пособии Введение в теорию метода конечных элементов
, а в 2014 г. описал их программную реализацию в издании Программная реализация метода конечных элементов в МATLAB
[15][16].
В книге Метод конечных элементов. Теория и задачи
(2008 г.) С. Трушин знакомит с методом конечных элементов в контексте решения прикладных задач. Описан также и алгоритм в общей форме. Рассматриваются вопросы статического расчета конструкций, устойчивости деформированного состояния систем, теплопередачи, динамики и механики жидкости. Описаны существующие методы решения нелинейных задач [17].
Книга А. Алямовского COSMOSWorks. Основы расчета конструкций в среде SolidWorks
(2010 г.) в большей степени рассказывает об использовании метода конечных элементов в системах автоматизированного проектирования, а именно о пакете COSMOSWorks, интегрированном в CAD-систему SolidWorks. Автор описал возможности системы в задачах инженерного расчёта прочности, выделил круг решаемых этим инструментом задач. Внимание акцентируется на проблемах области механики. Рассмотрены основные вопросы конечно-элементного моделирования: тонкостенные конструкции, соединения, контактная задача, термоупругость и тепловой расчёт. В качестве примеров приведены как расчёты канонических объектов, так и реальных производственных проектов. Даны советы по эффективной эксплуатации программного пакета для решения задач гидрогазодинамики и теплопередачи [18].
3.3. Обзор локальных источников
Учитывая роль Донецкого национального технического университета в развитии горной промышленности, он неразрывно связан с методом конечных элементов. Библиотека ДонНТУ насчитывает сотни публикаций, в которых в том или ином ключе встречаются понятия прочностный расчёт
, прогнозирование деформации сооружений
, температурный анализ
и пр.
Л. Лесик, Н. Дацун и О. Симоненко в работе Демонстрационная модель деформации металла (прокатка)
(1994 г.) описывают обучающую систему для студентов металлургических специальностей, которая в т. ч. содержит сведения о МКЭ и его применении [19].
В 2002 году В. Овсянников, В. Оверко и П. Зима опубликовали статью Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS
, где на примере объяснили алгоритм построения модели трубопровода и расчёта его состояния под воздействием нагрузок в программной системе конечно-элементного анализа ANSYS [20].
И. Сахно, С. Негрей и А. Лызенко посвятили МКЭ статью Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов
(2008 г.), в которой демонстрируется прогнозирование поведения разрушенных пород и сыпучих тел [21].
Методу конечных элементов также уделяется немало внимания и в выпускных работах магистров ДонНТУ. Среди них: Решение двумерных краевых задач параллельным методом конечных элементов
Хорошилова А. В. [22], Расчет барьерных целиков возле затопленных выработок
Климова А. А. [23], Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов
Скороходова Д. А. [24].
4. Введение в теорию МКЭ
Основные идеи МКЭ могут быть проиллюстрированы с помощью простейших краевых задач. Рассмотрим дифференциальное уравнение второго порядка с граничными условиями первого рода:
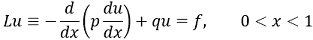 |
(1) |
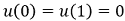 |
(2) |
Через ![C^k[0, 1]](images/formulas/inline/1.png) обозначим множество непрерывных и 𝑘 раз непрерывно дифференцируемых на отрезке [0, 1]. Через
обозначим множество непрерывных и 𝑘 раз непрерывно дифференцируемых на отрезке [0, 1]. Через ![C_0^k[0, 1]](images/formulas/inline/2.png) — множество функций, которые также обращаются в ноль на концах отрезка [0, 1]. Примем
— множество функций, которые также обращаются в ноль на концах отрезка [0, 1]. Примем ![p принадлежит C^1[0, 1]](images/formulas/inline/3.png) ,
, ![q и f принадлежат C[0, 1]](images/formulas/inline/4.png) , причём
, причём
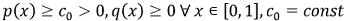 |
(3) |
Видоизменим уравнение (1), умножив его на функцию ![v принадлежит C_0^1[0, 1]](images/formulas/inline/5.png) , и проинтегрируем его по отрезку [0, 1].
, и проинтегрируем его по отрезку [0, 1].
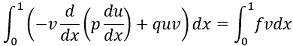 |
(4) |
Применив формулу интегрирования по частям, получим:
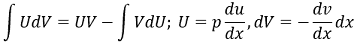 |
(5) |
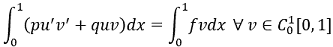 |
(6) |
Соотношение (6) является интегральным тождеством, соответствующим краевой задаче (1), (2). Если 𝑢 удовлетворяет тождеству (6), то оно есть решение задачи (1), (2), и наоборот [15].
Для приближённого решения задачи (1), (2) разобьём ось 𝑂𝑋 на 𝑛 равных частей длиной ℎ, введём множество базисных функций ![phi принадлежит C_0^1[0, 1]](images/formulas/inline/6.png) , которые равны нулю на всех значениях икса, кроме областей
, которые равны нулю на всех значениях икса, кроме областей ![[x_(i-1), x]](images/formulas/inline/7.png) , где они линейно растут от 0 до 1, и
, где они линейно растут от 0 до 1, и ![[x, x_(i+1)]](images/formulas/inline/8.png) , где линейно убывают от 1 до 0 (см. рис. 2):
, где линейно убывают от 1 до 0 (см. рис. 2):
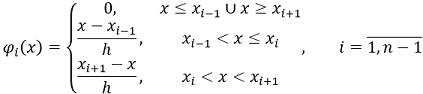 |
(7) |
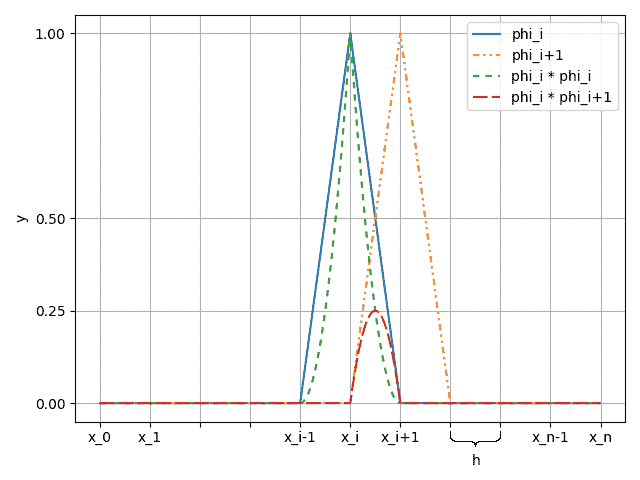
Рисунок 2 — Две соседние функции 𝜑(𝑥)
Прямая линия, полученная на каждом отрезке, есть конечный элемент. Один из примеров прикладного применения этого метода — предсказание прогиба натянутой струны, закреплённой в двух точках, под воздействием определённых сил.
Искомую функцию 𝑢 можно изобразить как:
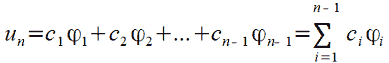 |
(8) |
Тогда соотношение (6) можно переписать в виде:
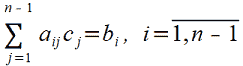 |
(9) |
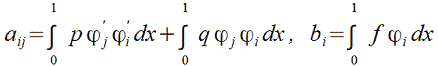 |
(10) |
Для простоты определим, что 𝑝 и 𝑞 — константы, и вычислим значения обоих интегралов 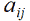 :
:
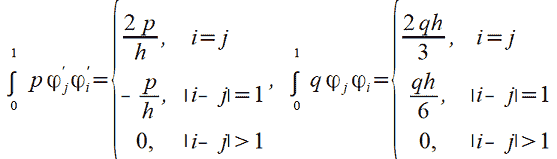 |
(11) |
Таким образом, имеем систему из 𝑛-1 линейных уравнений с 𝑛-1 неизвестными, решив которую, получим коэффициенты кусочно-линейной функции 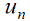 .
.
Выводы
Метод конечных элементов по сей день не теряет актуальности, занимая важное место во многих отраслях промышленности. Он применяется в решении задач прочности, упругости, гидрогазодинамики, распределения тепла и пр. Современные системы автоматизированного проектирования, пользующиеся спросом, включают в себя модули с реализацией МКЭ, что лишний раз подтверждает его востребованность.
В ходе работы над магистерской диссертацией на данный момент создана программа, позволяющая наглядно продемонстрировать работу МКЭ в простейшем случае — задаче о прогибе натянутой струны, закреплённой в двух точках, под воздействием определённых сил. В качестве входных параметров она принимает функции 𝑝, 𝑞 и 𝑓, границы исследуемого интервала 𝑥𝑙 и 𝑥𝑟, количество разбиений интервала 𝑛. В качестве результата возвращаются коэффициенты 𝑐 кусочно-линейной функции 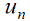 , а также строится график распределения сил (в соответствии с заданной функцией 𝑓) и предполагаемого прогиба струны.
, а также строится график распределения сил (в соответствии с заданной функцией 𝑓) и предполагаемого прогиба струны.
Ниже продемонстрированы результаты работы программы на некоторых наборах входных параметров: отображена зависимость точности приближения от количества разбиений интервала (см. рис. 3) и зависимость прогноза прогиба струны от величины прикладываемой силы (см. рис. 4). Синяя сплошная линия иллюстрирует распределение силы, оранжевый штрих-пунктир — прогноз прогиба струны под воздействием этой силы.
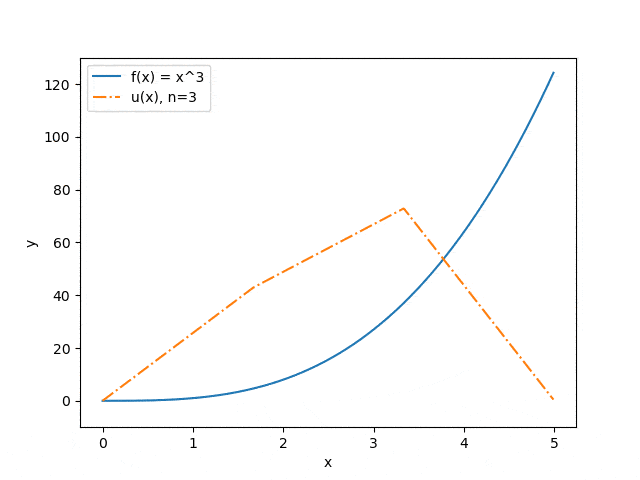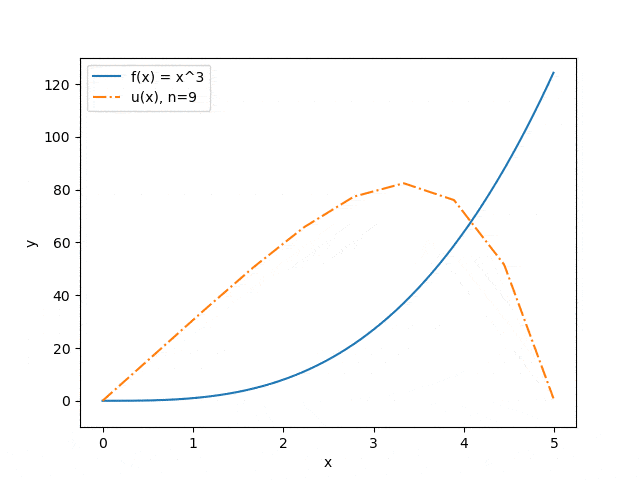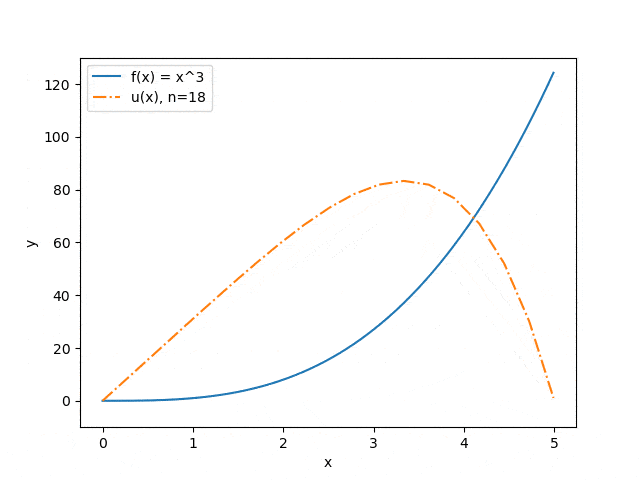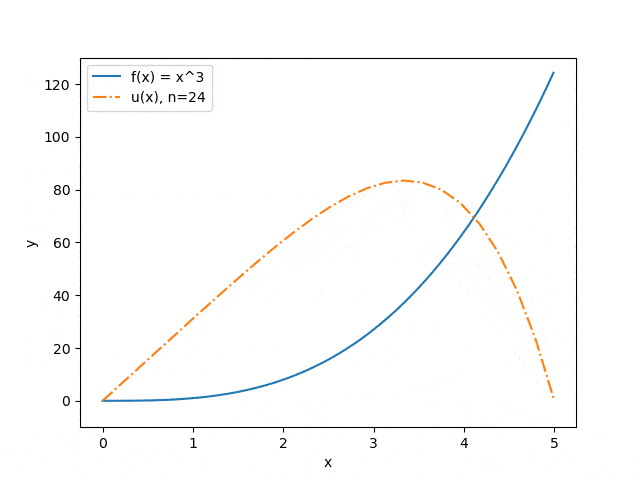
Рисунок 3 — Зависимость точности приближения от количества разбиений интервала
(анимация: 39.67 Кб, 640x480, 8 кадров, длительность кадра 200 мс, 10 циклов повторения)
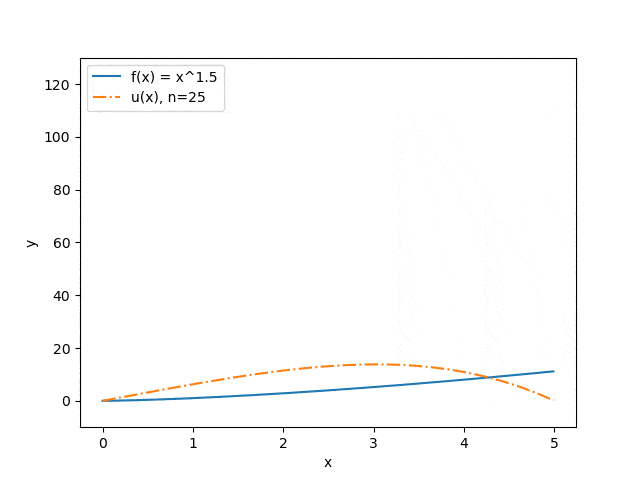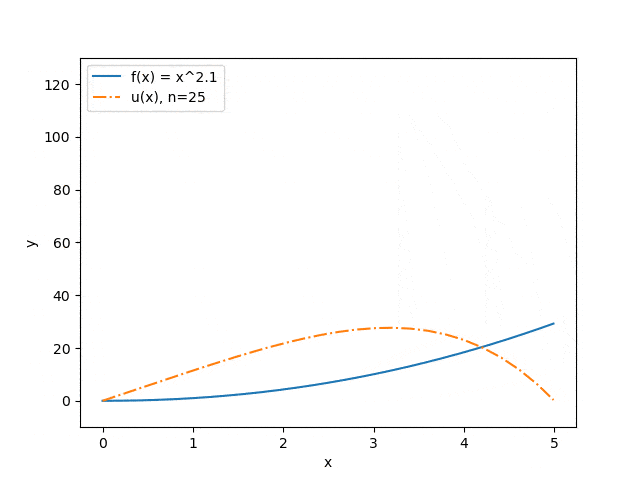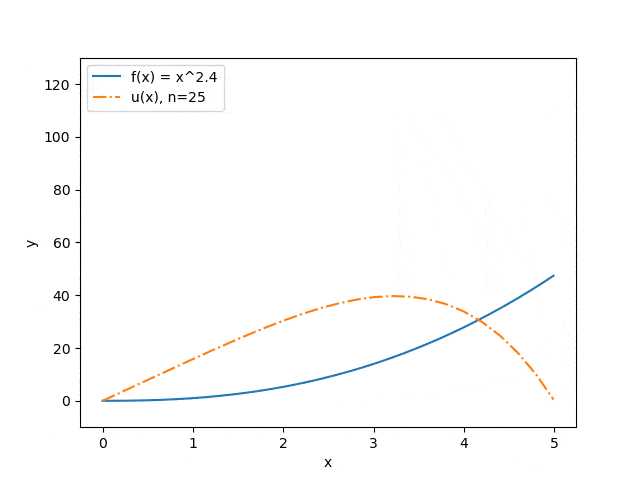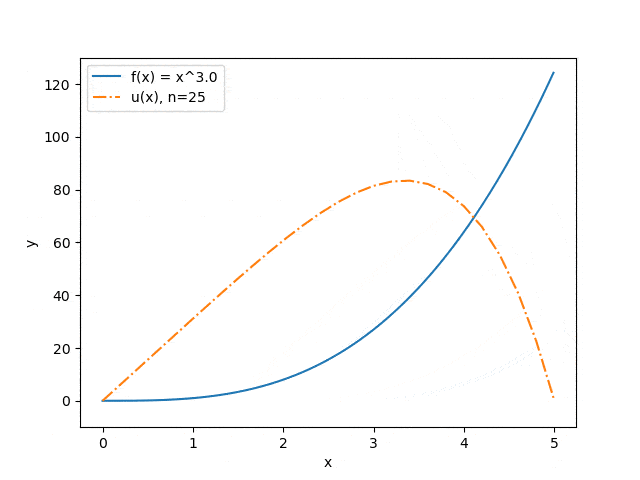
Рисунок 4 — Зависимость прогноза прогиба струны от величины прикладываемой силы
(анимация: 31.43 Кб, 640x480, 6 кадров, длительность кадра 400 мс, 10 циклов повторения)
Установлено, что в процессе обработки каждого конечного элемента выполняется одна и та же последовательность операций. Такая ситуация, когда требуется выполнять одинаковые инструкции снова и снова для большого количества входных данных, иначе говоря SIMD (single instruction, multiple data), является благоприятной для повышения производительности за счёт графических процессоров. Современные модели домашних центральных процессоров имеют на своём борту десятки вычислительных ядер, в то время как видеокарты — тысячи.
Даже в рассматриваемом простейшем случае задачи МКЭ выявлено несколько потенциальных участков для оптимизации. Во-первых, учитывая, что решение задачи подразумевает решение СЛАУ (системы линейных алгебраических уравнений), а количество уравнений может быть огромным, в контексте GPGPU (general-purpose computing on graphics processing units) очевидно напрашивается распараллеливание процесса формирования матрицы коэффициентов. Во-вторых, учитывая специфику МКЭ, можно быть уверенным в том, что матрица коэффициентов будет разрежённой, а именно — трёхдиагональной. Потому предлагается отказаться от привычного представления матриц в виде двумерных массивов, тем самым сэкономив не только время выполнения, а и объём потребляемой памяти. В-третьих, есть возможность выиграть на самом решении СЛАУ, возложив эту подзадачу на библиотеку cuSPARSE, которая содержит для этой цели готовые оптимизированные алгоритмы [25].
Список источников
- Секулович М. Метод конечных элементов / Пер. с серб. Ю. Н. Зуева; под ред. В. Ш. Барбакадзе. — М.: Стройиздат, 1993 — 664 с.: ил. — Перевод изд. Metid konacnih elemenata / Miodrag Sekulovic, 1988. — ISBN 5-274-01755-X.
- Шимановский А. Применение метода конечных элементов в решении задач прикладной механики : учеб.-метод. по собие для студентов технических специальностей / А. О. Шимановский, А. В. Путято ; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. — Гомель : БелГУТ, 2008. — 61 с. ISBN 978-985-468-474-1.
- Finite element method [Электронный ресурс] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=f... (дата обращения: 18.11.2020 г.).
- Метод конечных элементов [Электронный ресурс] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=м... (дата обращения: 18.11.2020 г.).
- Courant R. Variational methods for the solution of problems of equilibrium and vibrations / R. Courant // Bull. Amer. Math. Soc, 1943. vol 49(1). — pp. 1-23.
- Hrennikoff A. Solution of Problems of Elasticity by the Framework Method / A. Hrennikoff // Journal of Applied Mechanics, 1941. — vol 7(4). — pp. 0-0.
- Argyris J. Energy Theorems and Structural Analysis: A Generalized Discourse with Applications on Energy Principles of Structural Analysis Including the Effects of Temperature and Non‐Linear Stress‐Strain Relations Part I. General Theory / J. H. Argyris // Aircraft Engineering and Aerospace Technology, 1955. — vol 27(3). — pp. 80-94.
- Clough R. The Finite Element Method in Plane Stress Analysis / R. W. Clough. — American Society of Civil Engineers, 1960. — 35 pp.
- Knepley M. Finite Element Integration with Quadrature on the GPU / M. G. Knepley, K. Rupp, A. R. Terrel // CoRR, 2016. — vol. abs/1607.04245. — 14 pp.
- Monteiro A. A computational framework for G/XFEM material nonlinear analysis / A. B. Monteiro, A. R. V. Wolenski, F. B. Barros, R. L. S. Pitangueira, S. S.Penna // Advances in Engineering Software, 2017. — vol. 114. — pp. 380-393.
- Malekan M. Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach / M. Malekan, L. L. Silva, F. B. Barros, R. L. S. Pitangueira, S. S. Penna // Advances in Engineering Software, 2018. — vol. 115. — pp. 168-193.
- Kiran U. GPU-warp based finite element matrices generation and assembly using coloring method / U. Kiran, D. Sharma. S. S. Gautam // Journal of Computational Design and Engineering, 2019. — vol. 6(4). — pp. 705-718.
- Морозов Е. Метод конечных элементов в механике разрушения / Морозов Е. М., Никишков Г. П. — М.: Наука, 1980. — 256 с.
- Корягин Н. Пластическая деформация легких и специальных сплавов / Н. И. Корягин, А. Ф. Белов, А. С. Кузнецов и др. Пластическая деформация легких и специальных сплавов. Часть 2. — Сборник статей. — М.: Металлургия, 1982. — 201 с.
- Р. Даутов. Введение в теорию метода конечных элементов / Р. З. Даутов, М. М. Карчевский. — Учебное пособие. — Казань: КГУ, 2004. — 239 с.
- Р. Даутов. Программная реализация метода конечных элементов в МATLAB / Даутов Р. З. — Казань: КФУ, 2014. — 106 с.
- Трушин С. Метод конечных элементов. Теория и задачи / С. И. Трушин. — М.: АСВ, 2008. — 256 с.
- Алямовский А. COSMOSWorks. Основы расчета конструкций на прочность в среде SolidWorks / А. А. Алямовский. — ДМК Пресс, 2010. — ISBN 5-94074-582-2.
- Лесик Л. Демонстрационная модель деформации металла (прокатка) / Л. Н. Лесик, Н. Н. Дацун, О. А. Симоненко // Комп’ютерні програми учбового призначення: Тез. доп. II Міжнар. конф. (3-7 верес. 1994 р.). - Донецьк: ДонДУ, 1994. — с.115.
- Овсянниов В. Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS / В. П. Овсянников, В. М. Оверко, П. Ф. Зима // Наукові праці Донецького національного технічного університету. Серія: гірничо-електромеханічна. Випуск 51. - Донецьк: ДонНТУ, 2002.
- Негрей С. Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов / С. Г. Негрей, И. Г. Сахно, А. А. Лызенко // Новые технологии подземного строительства и добычи полезных ископаемых: Материалы между-народной научно-технической конференции. - Алчевск: ДонГТУ, 2008.
- Хорошилов А. Решение двумерных краевых задач параллельным методом конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2006/fvti/horoshilov/... (дата обращения: 11.11.2020 г.).
- Климов А. Расчет барьерных целиков возле затопленных выработок [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2008/ggeo/klimov/diss... (дата обращения: 11.11.2020 г.).
- Скороходов Д. Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2013/fmf/scorohodov/d... (дата обращения: 11.11.2020 г.).
- cuSPARSE [Электронный ресурс] // CUDA Toolkit Documentation. URL: https://docs.nvidia.com/cuda/cusparse/index.html (дата обращения: 06.10.2020 г.).
