Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Обзор существующих статистических методов анализа эмпирических данных
- 3.1. Графические методымоделей
- 3.2. Методы анализа статистических совокупностей
- 3.3. Экономическо-математические методы
- 4. Исследование зависимостей между эмпирическими данными
- 4.1. Корреляционный анализ
- 4.2. Дисперсионный анализ
- 4.3. Регрессионный анализ
- 5. Исследование зависимостей между эмпирическими данными
- Выводы
- Список источников
Введение
При проведении какого-либо исследования или эксперимента человеку необходимо проанализировать выходные данные для принятия дальнейших решений по поводу целесообразности этих исследования или экспериментов. Для этого существуют статистические методы. Однако для данные могут быть, как и разного типа, так и в большом диапазоне. Всё это влияет на выбор статистического метода для анализа эмпирических данных.
1. Актуальность темы
Электронное обучение, реализуемое образовательными организациями, должно включать в себя не только учебно-методические комплексы по дисциплинам (модулям), но и программное обеспечение, направленное на освоение профессиональных компетенций. Оптимальным способом формирования компетенций являются виртуальные лаборатории, смоделированные в электронной образовательной среде на объектах реального мира. [1]
Создание виртуальных лабораторий позволяет, с одной стороны, проводить эксперименты с оборудованием и материалами, соответствующими реальной лаборатории, с другой – ознакомиться с компьютерной моделью по освоению практических навыков и умений в профессиональной деятельности. Можно отметить, что не каждое образовательное учреждение может позволить себе закупить дорогостоящее оборудование, которое требует затрат при техническом обслуживании, приобретения расходных материалов, а главное, замены при его усовершенствовании. Универсальность виртуальных лабораторий компенсируют данные недостатки. [2]
Виртуальная лаборатория представляет студентам комплекс задач различных предметных областей, виртуальные инструменты для формализации условия процесса, средства для решения проблемы; учителям – постоянный контроль, диагностику освоения материала. Таким образом, студенты самостоятельно могут формировать практические умения и навыки в удобное для них время, не ограничивая себя временем и территориальной отдаленностью от образовательной организации.[3]
Так можно выделить главные преимущества виртуальных лабораторий от реальных:
- отсутствие необходимости приобретения дорогостоящего оборудования и реактивов;
- возможность моделирования процессов, протекание которых принципиально невозможно в лабораторных условиях;
- возможность проникновения в тонкости процессов и наблюдения происходящего в другом масштабе времени, что актуально для процессов, протекающих за доли секунды или, напротив, длящихся в течение нескольких лет;
- безопасность;
- в связи с тем, что управлением виртуального процесса занимается компьютер, появляется возможность быстрого проведения серии опытов с различными значениями входных параметров, что часто необходимо для определения зависимостей выходных параметров от входных;
- экономия времени и ресурсов для ввода результатов в электронный формат;
- возможность использования виртуальной лаборатории в дистанционном обучении, когда в принципе отсутствует возможность работы в лабораториях университета. [4]
2. Цель и задачи исследования
Целью исследования является создание виртуальной лаборатории для реализации анализа эмпирических данных статистическими методами. Для осуществления этой цели поставлены следующие задачи:
1. анализ области применения виртуальных лабораторий для работы с эмпирическими методами программной инженерии;
2. изучение и анализ существующих статистических методов для анализа эмпирических данных;
3. программная реализация виртуальной лаборатории;
4. оценка эффективности используемых методов обработки информации с помощью виртуальной лаборатории.
3. Обзор существующих статистических методов анализа эмпирических данных
Для решения задач, связанных с анализом данных (выявление скрытых взаимосвязей внутри массивов данных) при наличии случайных и непредсказуемых воздействий, математиками и другими исследователями за последние двести лет был выработан мощный и гибкий арсенал методов, называемых в совокупности статистическими методами анализа данных. За это время накоплен большой опыт успешного применения этих методов в разных сферах человеческой деятельности, от экономики до космических исследований. И при определенных условиях эти методы позволяют получать оптимальные решения. [5]
Статистические методы (методы, основанные на использовании математической статистики) являются эффективным инструментом сбора и анализа информации. Применение этих методов не требует больших затрат и позволяет с заданной степенью точности и достоверностью судить о состоянии исследуемых явлений (объектов, процессов), прогнозировать и регулировать проблемы на всех этапах их жизненного цикла и на основе этого вырабатывать оптимальные управленческие решения.
К настоящему времени в мировой практике накоплен огромный арсенал статистических методов, многие из которых могут быть достаточно эффективно использованы для решения различных вопросов.
Условно все методы можно классифицировать по признаку общности на три основные группы: графические методы, методы анализа статистических совокупностей и экономико-математические методы. Предложенная классификация не является ни универсальной, ни исчерпывающей, но она дает наглядное представление о разнообразии статистических методов и о тех потенциальных возможностях, которыми они располагают по части их использования при анализе данных.[6]
3.1. Графические методы
Графические методы основаны на применении графических средств анализа статистических данных. В эту группу могут быть включены такие методы, как контрольный листок, диаграмма Парето, схема Исикавы, гистограмма, диаграмма разброса, расслоение, контрольная карта, график временного ряда и др. Данные методы не требуют сложных вычислений, могут использоваться как самостоятельно, так и в комплексе с другими методами. Овладение ими не представляет особого труда не только для инженерно-технических работников, но и для специалистов низшего звена. Вместе с тем это весьма эффективные методы. Недаром они находят самое широкое применение в промышленности, особенно в работе групп качества.
3.2 Методы анализа статистических совокупностей
Методы анализа статистических совокупностей служат для исследования информации, когда изменение анализируемого параметра носит случайный характер. Основными методами, включаемыми в данную группу, являются: регрессивный, дисперсионный и факторный виды анализа, метод сравнения средних, метод сравнения дисперсий и др. Эти методы позволяют установить зависимость изучаемых явлений от случайных факторов как качественную (дисперсионный анализ), так и количественную (корреляционный анализ); исследовать связи между случайными и неслучайными величинами (регрессивный анализ); выявить роль отдельных факторов в изменении анализируемого параметра (факторный анализ) и т.д.
3.3 Экономическо-математические методы
Экономико-математические методы представляют собой сочетание экономических, математических и кибернетических методов. Центральным понятием методов этой группы является оптимизация, т. е. процесс нахождения наилучшего варианта из множества возможных с учетом принятого критерия (критерия оптимальности). Строго говоря, экономико-математические методы не являются чисто статистическими, но они широко используют аппарат математической статистики, что дает основание включить их в рассматриваемую классификацию статистических методов. Для целей, связанных с обеспечением качества, из достаточно обширной группы экономико-математических методов следует выделить в первую очередь следующие: математическое программирование (линейное, нелинейное, динамическое); планирование эксперимента; имитационное моделирование: теория игр; теория массового обслуживания; теория расписаний; функционально-стоимостной анализ и др. [7]
4. Исследование зависимостей между эмпирическими данными
Для исследования зависимости между эмпирическими данными используются корреляционный и дисперсионный анализ (для установления факта наличия или отсутствия зависимости между переменными), а также регрессионный анализ (для нахождения количественной зависимости между переменными).
4.1 Корреляционный анализ
Корреляционный анализ. Корреляция (Correlation) – связь между двумя или более переменными (в последнем случае корреляция называется множественной). Цель корреляционного анализа – установление наличия или отсутствия этой связи. В случае, когда имеются две переменные, значения которых измерены в шкале отношений, используется коэффициент линейной корреляции Пирсона r, который принимает значения от -1 до +1 (его нулевое значение свидетельствует об отсутствии корреляции). Термин «линейный» свидетельствует о том, что исследуется наличие линейной связи между переменными – если r(x, y) = 1, то одна переменная линейно зависит от другой (и наоборот), то есть существуют константы a и b, причем a > 0, такие что y = a x + b.
Для данных, измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена (он может применяться и для данных, измеренных в интервальной шкале, так как является непараметрическим и улавливает тенденцию – изменения переменных в одном направлении), который обозначается s и определяется сравнением рангов – номеров значений сравниваемых переменных в их упорядочении. Коэффициент корреляции Спирмена является менее чувствительным, чем коэффициент корреляции Пирсона (так как первый в случае измерений в шкале отношений учитывает лишь упорядочение x элементов выборки). В то же время он позволяет выявлять корреляцию между монотонно нелинейно связанными переменными (для которых коэффициент Пирсона может показывать незначительную корреляцию.
Универсальных рецептов установления корреляции между немонотонно и нелинейно связанными переменными на сегодняшний день не существует. Отметим, что большое (близкое к плюс единице или к минус единице) значение коэффициента корреляции говорит о связи переменных, но ничего не говорит о причинно-следственных отношениях между ними. [8]
4.2 Дисперсионный анализ
Дисперсионный анализ. Изучение наличия или отсутствия зависимости между переменными можно проводить и с помощью дисперсионного анализа (Analysis of Variance – ANOVA). Его суть заключается в следующем. Дисперсия характеризует «разброс» значений переменной. Переменные связаны, если для объектов, отличающихся значениями одной переменной, отличаются и значения другой переменной. Значит, нужно для всех объектов, имеющих одно и то же значение одной переменной (называемой независимой переменной), посмотреть, насколько различаются (насколько велика дисперсия) значения другой (или других) переменной, называемой зависимой переменной. Дисперсионный анализ как раз и дает возможность сравнить отношение дисперсии зависимой переменной (межгрупповой дисперсии) с дисперсией внутри групп объектов, характеризуемых одними и теми же значениями независимой переменной (внутригрупповой дисперсией). Другими словами, дисперсионный анализ «работает» следующим образом. Выдвигается гипотеза о наличии зависимости между переменными. Выделяются группы элементов выборки с одинаковыми значениями независимой переменной (число таких групп равно числу попарно различных значений независимой переменной). Если гипотеза о зависимости верна, то значения зависимой переменной внутри каждой группы должны не очень различаться (внутригрупповая дисперсия должна быть мала). Напротив, значения зависимой переменной для различных групп должны различаться сильно (межгрупповая дисперсия должна быть велика). То есть, переменные зависимы, если отношение межгрупповой дисперсии к внутригрупповой (обычно обозначаемое буквой F) велико. Если же гипотеза неверна, то это отношение должно быть мало.
4.3 Регрессионный анализ
Регрессионный анализ. Если корреляционный и дисперсионный анализ, качественно говоря, дают ответ на вопрос, существует ли взаимосвязь между переменными, то регрессионный анализ предназначен для того, чтобы найти «явный вид» этой зависимости. Цель регрессионного анализа – найти функциональную зависимость между переменными. Для этого предполагается, что зависимая переменная (иногда называемая откликом) определяется известной функцией (иногда говорят – моделью), зависящей от зависимой переменной или переменных (иногда называемых факторами) и некоторого параметра. Требуется найти такие значения этого параметра, чтобы полученная зависимость (модель) наилучшим образом описывала имеющиеся экспериментальные данные. Например, в простой линейной регрессии предполагается, что зависимая переменная y является линейной функцией y = a x + b от независимой переменной x. Требуется найти значения параметров a и b, при которых прямая ax + b будет наилучшим образом описывать (аппроксимировать) экспериментальные точки (x1, y1), (x2, y2), …, (xn, yn). [9]
5. Процесс исследования статистических методов для анализа данных в виртуальной лаборатории
Виртуальная лаборатория анализирует эмпирические данные каждым подходящими статистическими методами, при этом наглядно демонстрируя процесс анализа данных и его результат.
Главной особенностью виртуальной лаборатории является наглядность, а также результат сравнения методов. Это позволит пользователю в дальнейшем сделать вывод о эффективности каждого использованного метода с заданными эмпирическими данными. [10]
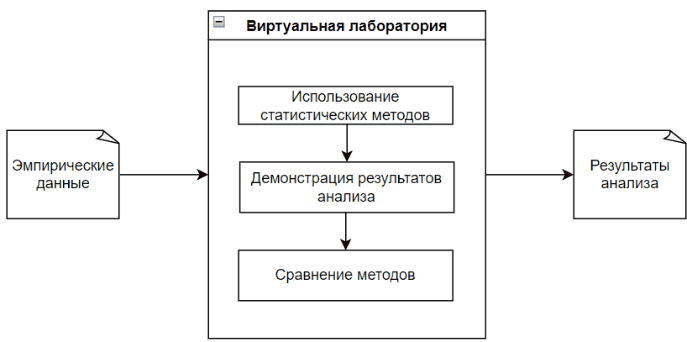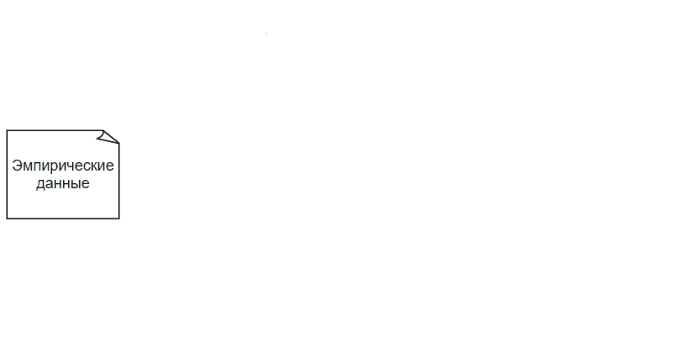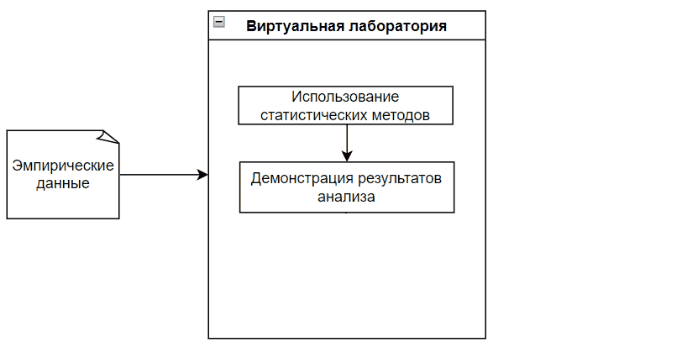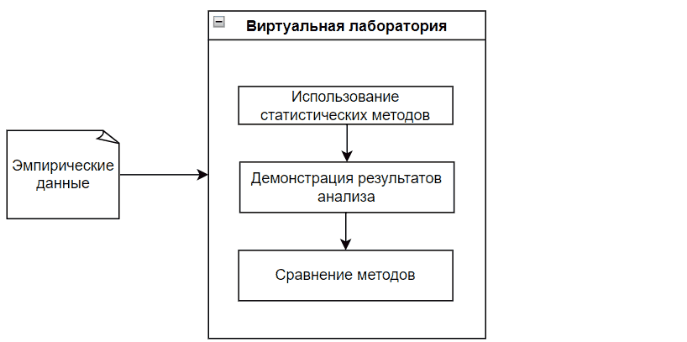 Рисунок 1 – Процесс работы виртуальной лаборатории (Рисунок анимирован, количество повторов неограниченно, 5 кадров, длительность одного составляет 1 с, вес файла – 57,2 КБ.)
Рисунок 1 – Процесс работы виртуальной лаборатории (Рисунок анимирован, количество повторов неограниченно, 5 кадров, длительность одного составляет 1 с, вес файла – 57,2 КБ.)
Вывод
В данном реферате была обоснованна актуальность использования виртуальных лабораторий. Была приведен обзор существующих статистических методов анализа эмпирических данных, а также способы исследования зависимостей между эмпирическими данными.
Разрабатываемая виртуальная лаборатория должна обеспечивать наглядность выполняемого исследования статистических методов, чтобы пользователь смог получить опыт работы с эмпирическими данными.
Список источников
- Болкунов, И. А., Электронное обучение: проблемы, перспективы, задачи / И. А. Болкунов. // Творческий научный обозреватель, №11, 2016. – С. 128-132.
- Саданова Б. М., Применение возможностей виртуальных лабораторий в учебном процессе технического вуза / Б. М. Саданова, А. В. Олейникова, И. В. Альберти [и др.]. — М.: Молодой ученый, 2016. — 74 с.
- Филь, Б.А. Эмпирические методы программной инженерии как курс в электронном обучении / Б.А. Филь, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках VII Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2021): XII Международная научно-техническая конференция, 26-27 мая 2021 – Донецк: ДонНТУ, 2021. – С. 466-468.
- Столбунская, А.С. Автоматизация процесса обучения при помощи виртуальных лабораторий / А.С. Столбунская, И.Д. Паламарчук, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2017): VIII Международная научно-техническая конференция, 25 мая 2017 – Донецк: ДонНТУ, 2017. – С. 406-409.
- Орлов, А. Прикладная статистика / А. Орлов. – М.:Экзамен, 2004. – 672 с.
- Глинский В. В., Ионин В. Г. Статистический анализ. — М.: Инфра-М, 2002. — 241 с.
- Орлов А. И. Прикладной статистический анализ: учебник. — М.: Ай Пи Ар Медиа, 2022. — 812 c.
- Ширяев А. Н. Статистический последовательный анализ. Оптимальные правила остановки — М.: Наука, 1976.
- Кендалл М., Стьюарт А. Многомерный статистический анализ и временные ряды. — М.: Наука, 1976. — 736 с.
- Принципы создания виртуальных лабораторий в инженерном образовании [Электронный ресурс]. – Режим доступа: https://sites.google.com/site/sredstvarazrabotkisimulacij/principy-sozdania-virtualnyh-laboratorij-v-inzenernom-obrazovanii
