RU   EN
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Під час проведення будь-якого дослідження чи експерименту людині необхідно проаналізувати вихідні дані прийняття подальших рішень щодо доцільності цих дослідження чи експериментів. І тому існують статистичні методи. Однак дані можуть бути, як і різного типу, так і у великому діапазоні. Все це впливає вибір статистичного методу для аналізу емпіричних даних.

1. Актуальность темы

Електронне навчання, що реалізується освітніми організаціями, повинно включати не лише навчально-методичні комплекси з дисциплін (модулів), але й програмне забезпечення, спрямоване на освоєння професійних компетенцій. Оптимальним способом формування компетенцій є віртуальні лабораторії, що змодельовані в електронному освітньому середовищі на об'єктах реального світу. [1]

Створення віртуальних лабораторій дозволяє, з одного боку, проводити експерименти з обладнанням та матеріалами, що відповідають реальній лабораторії, з іншого – ознайомитись з комп'ютерною моделлю щодо освоєння практичних навичок та умінь у професійній діяльності. Можна відзначити, що не кожна освітня установа може дозволити собі закупити дороге обладнання, яке потребує витрат при технічному обслуговуванні, придбання витратних матеріалів, а головне заміни при його вдосконаленні. Універсальність віртуальних лабораторій компенсують ці недоліки. [2]

Віртуальна лабораторія представляє студентам комплекс завдань різних предметних областей, віртуальні інструменти для формалізації умови процесу, засоби вирішення проблеми; учителям – постійний контроль, діагностику освоєння матеріалу. Таким чином, студенти самостійно можуть формувати практичні вміння та навички у зручний для них час, не обмежуючи себе часом та територіальною віддаленістю від освітньої організації. [3]

Так можна назвати основні переваги віртуальних лабораторій від реальних:

  • відсутність необхідності придбання дорогого обладнання та реактивів;
  • можливість моделювання процесів, перебіг яких принципово неможливий у лабораторних умовах;
  • можливість проникнення в тонкощі процесів та спостереження того, що відбувається в іншому масштабі часу, що актуально для процесів, що протікають за частки секунди або, навпаки, тривають протягом декількох років;
  • безпека;
  • у зв'язку з тим, що управлінням віртуального процесу займається комп'ютер, з'являється можливість швидкого проведення серії дослідів з різними значеннями вхідних параметрів, що часто необхідно визначення залежностей вихідних параметрів від вхідних;
  • економія часу та ресурсів для введення результатів в електронний формат;
  • можливість використання віртуальної лабораторії у дистанційному навчанні, коли в принципі відсутня можливість роботи у лабораторіях університету. [4]

2. Мета та завдання дослідження

Метою дослідження є створення віртуальної лабораторії для аналізу емпіричних даних статистичними методами. Для цієї мети поставлені такі задачи:

1. аналіз сфери застосування віртуальних лабораторій для роботи з емпіричними методами програмної інженерії;

2. вивчення та аналіз існуючих статистичних методів для аналізу емпіричних даних;

3. програмна реалізація віртуальної лабораторії;

4. оцінка ефективності використовуваних методів обробки інформації з допомогою віртуальної лабораторії.

3. Огляд існуючих статистичних методів аналізу емпіричних даних

Для вирішення завдань, пов'язаних з аналізом даних (виявлення прихованих взаємозв'язків усередині масивів даних) за наявності випадкових та непередбачуваних впливів, математиками та іншими дослідниками за останні двісті років був вироблений потужний та гнучкий арсенал методів, які називаються сукупністю статистичними методами аналізу даних. За цей час нагромаджено великий досвід успішного застосування цих методів у різних сферах людської діяльності, від економіки до космічних досліджень. І за певних умов ці методи дають змогу отримувати оптимальні рішення. [5]

Статистичні методи (методи, що ґрунтуються на використанні математичної статистики) є ефективним інструментом збору та аналізу інформації. Застосування цих методів не вимагає великих витрат і дозволяє із заданим ступенем точності та достовірністю судити про стан досліджуваних явищ (об'єктів, процесів), прогнозувати та регулювати проблеми на всіх етапах їх життєвого циклу та на основі цього виробляти оптимальні управлінські рішення.

На цей час у світовій практиці накопичено величезний арсенал статистичних методів, багато з яких може бути досить ефективно використані на вирішення різних питань.

Умовно всі методи можна класифікувати за ознакою спільності на три основні групи: графічні методи, методи аналізу статистичних сукупностей та економіко-математичні методи. Запропонована класифікація не є ні універсальною, ні вичерпною, але вона дає наочне уявлення про різноманітність статистичних методів і про ті потенційні можливості, які вони мають у частині їх використання при аналізі даних.[6]

3.1. Графічні методи

Графічні методи ґрунтуються на застосуванні графічних засобів аналізу статистичних даних. У цю групу можуть бути включені такі методи, як контрольний листок, діаграма Парето, схема Ісікави, гістограма, діаграма розкиду, розшарування, контрольна карта, графік тимчасового ряду та ін. Дані методи не вимагають складних обчислень, можуть використовуватися як самостійно, так і комплекс з іншими методами. Опанування ними не становить особливих труднощів не тільки для інженерно-технічних працівників, але і для фахівців нижчої ланки. Водночас це дуже ефективні методи. Недарма вони знаходять найширше застосування у промисловості, особливо у роботі груп якості.

3.2 Методи аналізу статистичних сукупностей

Методи аналізу статистичних сукупностей служать вивчення інформації, коли зміна аналізованого параметра носить випадковий характер. Основними методами, що включаються до цієї групи, є: регресивний, дисперсійний і факторний види аналізу, метод порівняння середніх, метод порівняння дисперсій та ін. аналіз); дослідити зв'язки між випадковими та невипадковими величинами (регресивний аналіз); виявити роль окремих факторів у зміні аналізованого параметра (факторний аналіз) тощо.

3.3 Економічно-математичні методи

Економіко-математичні методи є поєднанням економічних, математичних і кібернетичних методів. Центральним поняттям методів цієї групи є оптимізація, тобто процес знаходження найкращого варіанта з безлічі можливих з урахуванням прийнятого критерію (критерію оптимальності). Строго кажучи, економіко-математичні методи не є чисто статистичними, але вони широко використовують апарат математичної статистики, що дає підставу включити їх у класифікацію статистичних методів, що розглядається. Для цілей, пов'язаних із забезпеченням якості, із досить великої групи економіко-математичних методів слід виділити насамперед такі: математичне програмування (лінійне, нелінійне, динамічне); планування експерименту; імітаційне моделювання: теорія ігор; теорія масового обслуговування; теорія розкладів; функціонально-вартісний аналіз та ін. [7]

4. Дослідження залежностей між емпіричними даними

Для дослідження залежності між емпіричними даними використовуються кореляційний та дисперсійний аналіз (для встановлення факту наявності чи відсутності залежності між змінними), а також регресійний аналіз (для знаходження кількісної залежності між змінними).

4.1 Кореляційний аналіз

Кореляційний аналіз. Кореляція (Correlation) – зв'язок між двома або більше змінними (в останньому випадку кореляція називається множинною). Мета кореляційного аналізу – встановлення наявності чи відсутності зв'язку. У разі, коли є дві змінні, значення яких виміряно в шкалі відносин, використовується коефіцієнт лінійної кореляції Пірсона r, який набуває значення від -1 до +1 (його нульове значення свідчить про відсутність кореляції). Термін «лінійний» свідчить про те, що досліджується наявність лінійного зв'язку між змінними – якщо r(x, y) = 1, то одна змінна лінійно залежить від іншої (і навпаки), тобто існують константи a та b, причому a > 0 , Такі що y = a x + b.

Для даних, виміряних у порядковій шкалі, слід використовувати коефіцієнт рангової кореляції Спірмена (він може застосовуватися і для даних, виміряних в інтервальній шкалі, оскільки є непараметричним і вловлює тенденцію – зміни змінних в одному напрямку), який позначається s і визначається порівнянням рангів – номерів значень порівнюваних змінних у тому упорядкуванні. Коефіцієнт кореляції Спірмена менш чутливим, ніж коефіцієнт кореляції Пірсона (оскільки перший у разі вимірів у шкалі відносин враховує лише впорядкування x елементів вибірки). У той самий час він дозволяє виявляти кореляцію між монотонно нелінійно пов'язаними змінними ( котрим коефіцієнт Пірсона може показувати незначну кореляцію.

Універсальних рецептів встановлення кореляції між немонотонно та нелінійно пов'язаними змінними на сьогоднішній день не існує. Зазначимо, що велике (близьке до плюс одиниці або мінус одиниці) значення коефіцієнта кореляції говорить про зв'язок змінних, але нічого не говорить про причинно-наслідкові відносини між ними. [8]

4.2 Дисперсійний аналіз

Дисперсійний аналіз. Вивчення наявності чи відсутності залежності між змінними можна проводити за допомогою дисперсійного аналізу (Analysis of Variance - ANOVA). Його суть полягає у наступному. Дисперсія характеризує «розкид» значень змінної. Змінні пов'язані, якщо для об'єктів, що відрізняються значеннями однієї змінної, відрізняються значення іншої змінної. Отже, потрібно всім об'єктів, мають одне й те значення однієї змінної (званої незалежної змінної), подивитися, наскільки різняться (наскільки велика дисперсія) значення інший (чи інших) змінної, званої залежної змінної. Дисперсійний аналіз якраз і дає можливість порівняти відношення дисперсії залежної змінної (міжгрупової дисперсії) з дисперсією всередині груп об'єктів, що характеризуються одними й тими самими значеннями незалежної змінної (внутрішньогрупової дисперсії). Інакше кажучи, дисперсійний аналіз «працює» в такий спосіб. Висувається гіпотеза про наявність залежності між змінними. Виділяються групи елементів вибірки з однаковими значеннями незалежної змінної (кількість таких груп дорівнює числу попарно різних значень незалежної змінної). Якщо гіпотеза про залежність вірна, то значення залежної змінної всередині кожної групи повинні не дуже відрізнятися (внутрішньогрупова дисперсія має бути мала). Навпаки, значення залежної змінної різних груп повинні відрізнятися сильно (міжгруппова дисперсія має бути велика). Тобто змінні залежні, якщо відношення міжгрупової дисперсії до внутрішньогрупової (зазвичай позначається буквою F) велике. Якщо ж гіпотеза неправильна, це ставлення має бути мало.

4.3 Регресійний аналіз

Регресійний аналіз. Якщо кореляційний та дисперсійний аналіз, якісно кажучи, дають відповідь на питання, чи існує взаємозв'язок між змінними, то регресійний аналіз призначений для того, щоб знайти «явний вигляд» цієї залежності. Мета регресійного аналізу – знайти функціональну залежність між змінними. Для цього передбачається, що залежна змінна (іноді звана відгуком) визначається відомою функцією (іноді говорять – моделлю), яка залежить від залежної змінної або змінних (іноді званих факторами) і деякого параметра. Потрібно знайти такі значення цього параметра, щоб отримана залежність (модель) найкраще описувала наявні експериментальні дані. Наприклад, у простій лінійній регресії передбачається, що залежна змінна y є лінійною функцією y = a x + b від незалежної змінної x. Потрібно знайти значення параметрів a і b, у яких пряма ax + b найкраще описувати (апроксимувати) експериментальні точки (x1, y1), (x2, y2), …, (xn, yn). [9]

5. Процес дослідження статистичних методів для аналізу даних у віртуальній лабораторії

Віртуальна лабораторія аналізує емпіричні дані кожним відповідними статистичними методами, при цьому наочно демонструючи процес аналізу даних та його результат.

Головною особливістю віртуальної лабораторії є наочність, і навіть результат порівняння методів. Це дозволить користувачеві надалі зробити висновок про ефективність кожного використаного методу із заданими емпіричними даними. [10]

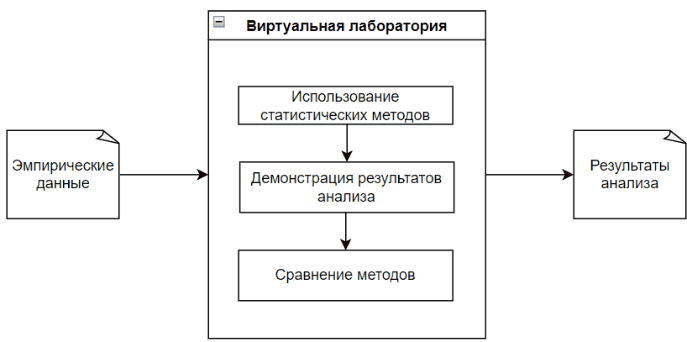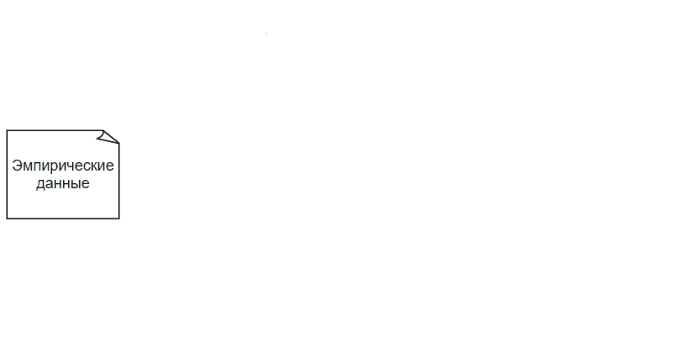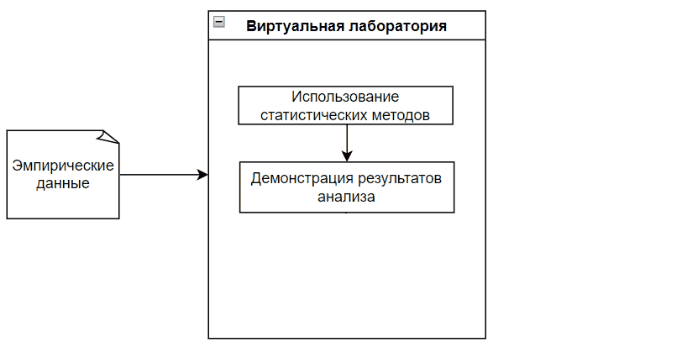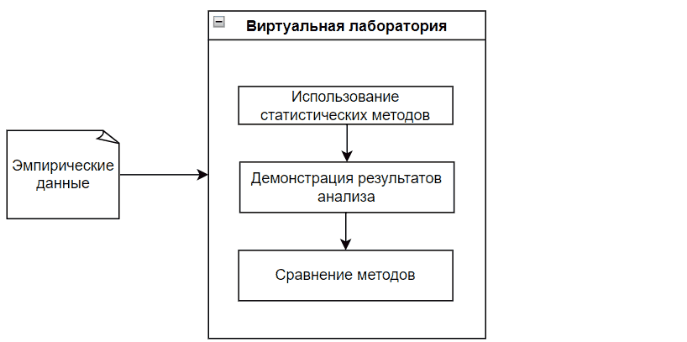Малюнок 1 – Процес роботи віртуальної лабораторії (Малюнок анімований, кількість повторів необмежена, 5 кадрів, тривалість одного становить 1 с, вага файлу – 57,2 КБ.)

Висновки

У цьому рефераті було обгрунтовано актуальність використання віртуальних лабораторій. Наведено огляд існуючих статистичних методів аналізу емпіричних даних, а також способи дослідження залежностей між емпіричними даними.

Віртуальна лабораторія, що розробляється, повинна забезпечувати наочність виконуваного дослідження статистичних методів, щоб користувач зміг отримати досвід роботи з емпіричними даними.

Список джерел

  1. Болкунов, И. А., Электронное обучение: проблемы, перспективы, задачи / И. А. Болкунов. // Творческий научный обозреватель, №11, 2016. – С. 128-132.
  2. Саданова Б. М., Применение возможностей виртуальных лабораторий в учебном процессе технического вуза / Б. М. Саданова, А. В. Олейникова, И. В. Альберти [и др.]. — М.: Молодой ученый, 2016. — 74 с.
  3. Филь, Б.А. Эмпирические методы программной инженерии как курс в электронном обучении / Б.А. Филь, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках VII Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2021): XII Международная научно-техническая конференция, 26-27 мая 2021 – Донецк: ДонНТУ, 2021. – С. 466-468.
  4. Столбунская, А.С. Автоматизация процесса обучения при помощи виртуальных лабораторий / А.С. Столбунская, И.Д. Паламарчук, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2017): VIII Международная научно-техническая конференция, 25 мая 2017 – Донецк: ДонНТУ, 2017. – С. 406-409.
  5. Орлов, А. Прикладная статистика / А. Орлов. – М.:Экзамен, 2004. – 672 с.
  6. Глинский В. В., Ионин В. Г. Статистический анализ. — М.: Инфра-М, 2002. — 241 с.
  7. Орлов А. И. Прикладной статистический анализ: учебник. — М.: Ай Пи Ар Медиа, 2022. — 812 c.
  8. Ширяев А. Н. Статистический последовательный анализ. Оптимальные правила остановки — М.: Наука, 1976.
  9. Кендалл М., Стьюарт А. Многомерный статистический анализ и временные ряды. — М.: Наука, 1976. — 736 с.
  10. Принципы создания виртуальных лабораторий в инженерном образовании [Электронный ресурс]. – Режим доступа: https://sites.google.com/site/sredstvarazrabotkisimulacij/principy-sozdania-virtualnyh-laboratorij-v-inzenernom-obrazovanii