Abstract
Content
- Introduction
- 1. Relevance of the topic
- 2. Purpose and objectives of the study
- 3. Review of existing statistical methods for the analysis of empirical data
- 3.1. Graphic Methods
- 3.2. Methods for analyzing statistical populations
- 3.3. Economic and mathematical methods
- 4. Study of dependencies between empirical data
- 4.1. Correlation analysis
- 4.2. Analysis of variance
- 4.3. Regression analysis
- 5. The process of researching statistical methods for data analysis in a virtual laboratory
- Conclusions
- List of sources
Introduction
When conducting any study or experiment, a person needs to analyze the output data to make further decisions about the appropriateness of this study or experiments. There are statistical methods for this. However, the data can be both of different types and in a large range. All this affects the choice of a statistical method for the analysis of empirical data.
1. Relevance of the topic
E-learning implemented by educational organizations should include not only educational and methodological complexes in disciplines (modules), but also software aimed at mastering professional competencies. The best way to form competencies is virtual laboratories, modeled in an electronic educational environment on real world objects. [1]
The creation of virtual laboratories allows, on the one hand, to conduct experiments with equipment and materials corresponding to a real laboratory, on the other hand, to get acquainted with a computer model for mastering practical skills and abilities in professional activities. It can be noted that not every educational institution can afford to purchase expensive equipment that requires maintenance costs, the purchase of consumables, and most importantly, replacement when it is improved. The versatility of virtual laboratories compensates for these shortcomings. [2]
The virtual laboratory presents students with a set of tasks of various subject areas, virtual tools for formalizing the conditions of the process, means for solving the problem; teachers - constant monitoring, diagnostics of mastering the material. Thus, students can independently form practical skills at a convenient time for them, without limiting themselves to time and territorial remoteness from the educational organization. [3]
We can distinguish such main advantages of virtual laboratories from real ones as:
- no need to purchase expensive equipment and reagents;
- the possibility of modeling processes, the course of which is fundamentally impossible in laboratory conditions;
- the ability to delve into the intricacies of processes and observe what is happening on a different time scale, which is relevant for processes that occur in a fraction of a second or, on the contrary, last for several years;
- security;
- due to the fact that the virtual process is controlled by a computer, it becomes possible to quickly conduct a series of experiments with different values of input parameters, which is often necessary to determine the dependences of output parameters on input ones;
- saving time and resources for entering results into an electronic format;
- ? the possibility of using a virtual laboratory in distance learning, when in principle there is no possibility of working in the laboratories of the university. [4]
2. Purpose and objectives of the study
The aim of the study is to create a virtual laboratory for the implementation of the analysis of empirical data by statistical methods. To achieve this goal, the following tasks have been set:
1. analysis of the scope of virtual laboratories for working with empirical methods of software engineering;
2. study and analysis of existing statistical methods for the analysis of empirical data;
3. software implementation of the virtual laboratory;
4. Evaluation of the effectiveness of the information processing methods used with the help of a virtual laboratory.
3. Review of existing statistical methods for the analysis of empirical data
To solve problems related to data analysis (identifying hidden relationships within data arrays) in the presence of random and unpredictable influences, mathematicians and other researchers have developed a powerful and flexible arsenal of methods over the past two hundred years, collectively called statistical methods of data analysis. During this time, a lot of experience has been accumulated in the successful application of these methods in various fields of human activity, from economics to space research. And under certain conditions, these methods make it possible to obtain optimal solutions. [5]
Statistical methods (methods based on the use of mathematical statistics) are an effective tool for collecting and analyzing information. The use of these methods does not require large expenditures and makes it possible to judge the state of the studied phenomena (objects, processes) with a given degree of accuracy and reliability, predict and regulate problems at all stages of their life cycle, and, on the basis of this, develop optimal management decisions.
To date, a huge arsenal of statistical methods has been accumulated in world practice, many of which can be quite effectively used to solve various problems.
Conventionally, all methods can be classified on the basis of generality into three main groups: graphical methods, methods for analyzing statistical populations, and economic and mathematical methods. The proposed classification is neither universal nor exhaustive, but it gives a visual representation of the variety of statistical methods and the potential they have in terms of their use in data analysis.[6]
3.1. Graphic Methods
Graphical methods are based on the use of graphical analysis tools for statistical data. This group may include methods such as a checklist, Pareto chart, Ishikawa scheme, histogram, scatter plot, stratification, control chart, time series graph, etc. These methods do not require complex calculations, can be used both independently and in in combination with other methods. Mastering them is not difficult not only for engineering and technical workers, but also for lower-level specialists. However, these are very effective methods. No wonder they are widely used in industry, especially in the work of quality groups.
3.2 Methods for analyzing statistical populations
Methods for analyzing statistical populations are used to study information when the change in the analyzed parameter is random. The main methods included in this group are: regression, variance and factor analysis, the method of comparing averages, the method of comparing variances, etc. These methods allow you to establish the dependence of the studied phenomena on random factors, both qualitative (variance analysis) and quantitative (correlation analysis). analysis); explore relationships between random and non-random variables (regression analysis); identify the role of individual factors in changing the analyzed parameter (factorial analysis), etc.
3.3 Economic and mathematical methods
Economic-mathematical methods are a combination of economic, mathematical and cybernetic methods. The central concept of the methods of this group is optimization, i.e., the process of finding the best option from a set of possible ones, taking into account the accepted criterion (optimality criterion). Strictly speaking, economic and mathematical methods are not purely statistical, but they widely use the apparatus of mathematical statistics, which gives reason to include them in the considered classification of statistical methods. For purposes related to quality assurance, from a fairly large group of economic and mathematical methods, the following should be singled out in the first place: mathematical programming (linear, non-linear, dynamic); experiment planning; simulation modeling: game theory; queuing theory; scheduling theory; functional cost analysis, etc. [7]
4. Study of dependencies between empirical data
To study the relationship between empirical data, correlation and variance analysis are used (to establish the fact of the presence or absence of a relationship between variables), as well as regression analysis (to find a quantitative relationship between variables).
4.1 Correlation analysis
Correlation analysis. Correlation - the relationship between two or more variables (in the latter case, the correlation is called multiple). The purpose of correlation analysis is to establish the presence or absence of this relationship. In the case when there are two variables whose values are measured on a ratio scale, Pearson's linear correlation coefficient r is used, which takes values from -1 to +1 (its value of zero indicates no correlation). The term "linear" indicates that the presence of a linear relationship between variables is being investigated - if r(x, y) = 1, then one variable depends linearly on the other (and vice versa), that is, there are constants a and b, and a > 0 , such that y = a x + b.
For data measured on an ordinal scale, Spearman's rank correlation coefficient should be used (it can also be used for data measured on an interval scale, as it is non-parametric and captures a trend - changes in variables in one direction), which is denoted by s and is determined by comparing ranks - numbers of values of compared variables in their ordering. Spearman's correlation coefficient is less sensitive than Pearson's correlation coefficient (because the former, in the case of measurements in the ratio scale, takes into account only the x ordering of the sample elements). At the same time, it allows one to detect correlations between monotonically non-linearly related variables (for which the Pearson coefficient may show little correlation.
Today, there are no universal recipes for establishing a correlation between nonmonotonically and non-linearly related variables. Note that a large (close to plus one or minus one) value of the correlation coefficient indicates the relationship of the variables, but says nothing about the cause-and-effect relationship between them. [8]
4.2 Analysis of variance
Dispersion analysis. The study of the presence or absence of a relationship between variables can also be carried out using analysis of variance (Analysis of Variance - ANOVA). Its essence is as follows. Dispersion characterizes the "scatter" of the values of a variable. Variables are related if for objects that differ in the values of one variable, the values of another variable also differ. So, for all objects that have the same value of one variable (called the independent variable), it is necessary to look at how much the values of another (or other) variable, called the dependent variable, differ (how large the dispersion is). Analysis of variance just makes it possible to compare the ratio of the variance of the dependent variable (intergroup variance) with the variance within groups of objects characterized by the same values of the independent variable (intragroup variance). In other words, the analysis of variance "works" as follows. A hypothesis is put forward about the presence of a relationship between the variables. Groups of sample elements with the same values of the independent variable are identified (the number of such groups is equal to the number of pairwise different values of the independent variable). If the dependence hypothesis is true, then the values of the dependent variable within each group should not differ much (within-group variance should be small). On the contrary, the values of the dependent variable for different groups should differ greatly (between-group variance should be large). That is, the variables are dependent if the ratio of between-group to within-group variance (usually denoted by the letter F) is large. If the hypothesis is false, then this ratio should be small.
4.3 Regression analysis
Regression analysis. If correlation and variance analysis, qualitatively speaking, give an answer to the question of whether there is a relationship between variables, then regression analysis is designed to find the "explicit form" of this relationship. The purpose of regression analysis is to find a functional relationship between variables. This assumes that the dependent variable (sometimes called the response) is determined by a known function (sometimes called a model) that depends on the dependent variable or variables (sometimes called factors) and some parameter. It is required to find such values of this parameter that the obtained dependence (model) best describes the available experimental data. For example, in simple linear regression, the dependent variable y is assumed to be a linear function of y = ax + b of the independent variable x. It is required to find the values of the parameters a and b for which the straight line ax + b will best describe (approximate) the experimental points (x1, y1), (x2, y2), …, (xn, yn). [9]
5. The process of researching statistical methods for data analysis in a virtual laboratory
The Virtual Lab analyzes empirical data with each appropriate statistical method, while visually demonstrating the data analysis process and its result.
The main feature of the virtual laboratory is visibility, as well as the result of comparing methods. This will allow the user to further conclude on the effectiveness of each method used with given empirical data. [10]
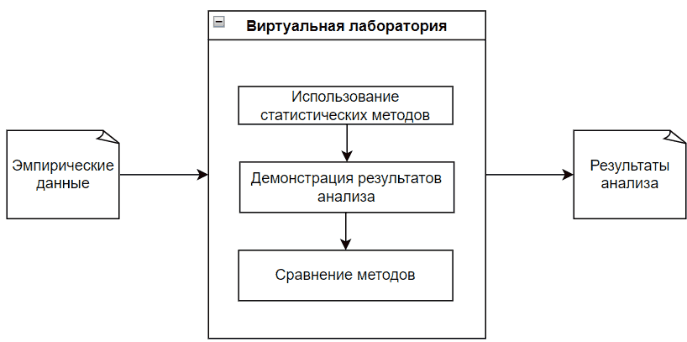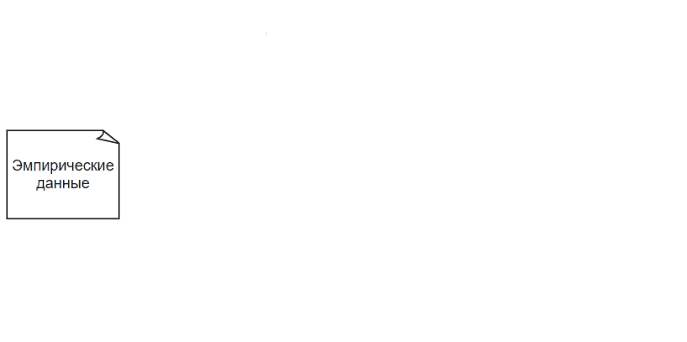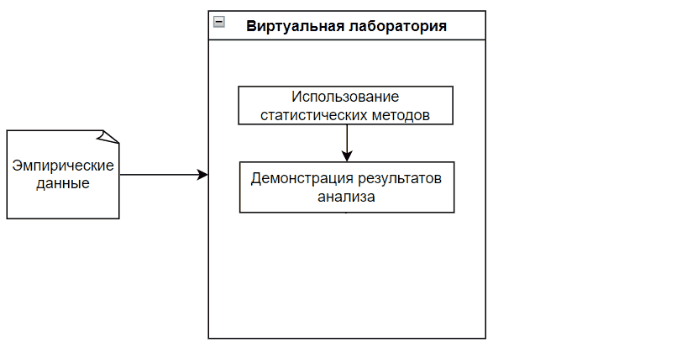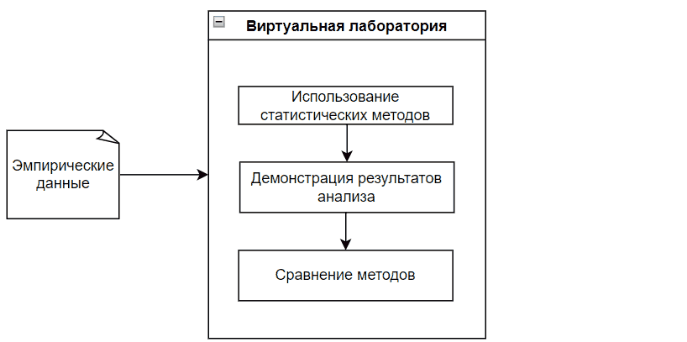 Figure 1 - The process of the virtual laboratory (The figure is animated, the number of repetitions is unlimited, 5 frames, the duration of one frame is 1 s, the file weight is 57.2 KB.)
Figure 1 - The process of the virtual laboratory (The figure is animated, the number of repetitions is unlimited, 5 frames, the duration of one frame is 1 s, the file weight is 57.2 KB.)
Conclusions
In this essay, the relevance of using virtual laboratories was substantiated. An overview of existing statistical methods for analyzing empirical data was given, as well as ways to study the relationships between empirical data.
The virtual laboratory being developed should provide visibility into the study of statistical methods, so that the user can gain experience working with empirical data.
List of sources
- Болкунов, И. А., Электронное обучение: проблемы, перспективы, задачи / И. А. Болкунов. // Творческий научный обозреватель, №11, 2016. – С. 128-132.
- Саданова Б. М., Применение возможностей виртуальных лабораторий в учебном процессе технического вуза / Б. М. Саданова, А. В. Олейникова, И. В. Альберти [и др.]. — М.: Молодой ученый, 2016. — 74 с.
- Филь, Б.А. Эмпирические методы программной инженерии как курс в электронном обучении / Б.А. Филь, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках VII Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2021): XII Международная научно-техническая конференция, 26-27 мая 2021 – Донецк: ДонНТУ, 2021. – С. 466-468.
- Столбунская, А.С. Автоматизация процесса обучения при помощи виртуальных лабораторий / А.С. Столбунская, И.Д. Паламарчук, Д.М. Бочаров // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2017): VIII Международная научно-техническая конференция, 25 мая 2017 – Донецк: ДонНТУ, 2017. – С. 406-409.
- Орлов, А. Прикладная статистика / А. Орлов. – М.:Экзамен, 2004. – 672 с.
- Глинский В. В., Ионин В. Г. Статистический анализ. — М.: Инфра-М, 2002. — 241 с.
- Орлов А. И. Прикладной статистический анализ: учебник. — М.: Ай Пи Ар Медиа, 2022. — 812 c.
- Ширяев А. Н. Статистический последовательный анализ. Оптимальные правила остановки — М.: Наука, 1976.
- Кендалл М., Стьюарт А. Многомерный статистический анализ и временные ряды. — М.: Наука, 1976. — 736 с.
- Принципы создания виртуальных лабораторий в инженерном образовании [Электронный ресурс]. – Режим доступа: https://sites.google.com/site/sredstvarazrabotkisimulacij/principy-sozdania-virtualnyh-laboratorij-v-inzenernom-obrazovanii
