Реферат по теме выпускной работы

Содержание

• Введение
• 1. Потери мощности в элементах сети
• 2. Расчет потерь мощности в линиях электропередач
• 3. Расчет потерь мощности в трансформаторах
• 4. Недетерминированная модель электрической нагрузки
• 5. Мероприятия по снижению потерь мощности
• 6. Расчет потерь электроэнергии
• 7. Задача расчета режимов. Основные допущения
• 8. Баланс мощностей в энергосистеме
• Список источников

Введение

Электрическая мощность ‒ физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).

1. Потери мощности в элементах сети

Для количественной характеристики работы элементов электрической сети рассматриваются ее рабочие режимы. Рабочий режим – это установившееся электрическое состояние, которое характеризуется значениями токов, напряжений, активной, реактивной и полной мощностей.

Основной целью расчета режимов является определение этих параметров, как для проверки допустимости режимов, так и для обеспечения экономичности работы элементов сетей [1].

Определение значений токов в элементах сети и напряжений в ее узлах начинается с построения картины распределения полной мощности по элементу, т.е. с определения мощностей в начале и конце каждого элемента. Такую картину называют потокораспределением.

Рассчитывая мощности в начале и в конце элемента электрической сети, учитывают потери мощности в сопротивлениях элемента и влияние его проводимостей [2].

2. Расчет потерь мощности в линиях электропередач

Потери активной мощности на участке ЛЭП (рис.1) обусловлены активным сопротивлением проводов и кабелей, а также несовершенством их изоляции. Мощность, теряемая в активных сопротивлениях трехфазной ЛЭП и расходуемая на ее нагрев, определяется по формуле:

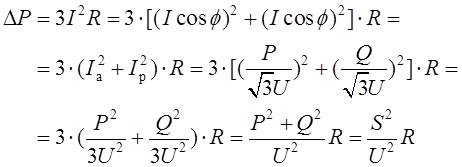
где I, Ia, Ip ‒ полный, активный и реактивный токи в ЛЭП;
P, Q, S – активная, реактивная и полная мощности в начале или конце ЛЭП;
U – линейное напряжение в начале или конце ЛЭП;
R – активное сопротивление одной фазы ЛЭП.

Рисунок 1 – К расчету потерь мощности на участке электрической сети

Потери активной мощности в проводимостях ЛЭП обусловлены несовершенством изоляции. В воздушных ЛЭП – появлением короны и, в очень незначительной степени, утечкой тока по изоляторам. В кабельных ЛЭП – появлением тока проводимости а его абсорбции. Рассчитываются потери по формуле:

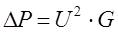
где U – линейное напряжение в начале или конце ЛЭП;
G – активная проводимость ЛЭП.

При проектировании воздушных ЛЭП потери мощности на корону стремятся свести к нулю, выбирая такой диаметр провода, когда возможность возникновения короны практически отсутствует.

Потери реактивной мощности на участке ЛЭП обусловлены индуктивными сопротивлениями проводов и кабелей. Реактивная мощность, теряемая в трехфазной ЛЭП, рассчитывается аналогично мощности, теряемой в активных сопротивлениях:

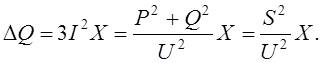
Генерируемая емкостной проводимостью зарядная мощность ЛЭП рассчитывается по формуле [3]:

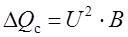
где U – линейное напряжение в начале или конце ЛЭП;
B – реактивная проводимость ЛЭП.

Зарядная мощность уменьшает реактивную нагрузку сети и тем самым снижает потери мощности в ней.

3. Расчет потерь мощности в трансформаторах

Потери активной и реактивной мощности в трансформаторах и автотрансформаторах разделяются на потери в стали и потери в меди (нагрузочные потери). Потери в стали – это потери в проводимостях трансформаторов. Они зависят от приложенного напряжения. Нагрузочные потери – это потери в сопротивлениях трансформаторов. Они зависят от тока нагрузки.

Потери активной мощности в стали трансформаторов – это потери на перемагничивание и вихревые токи [4]. Определяются потерями холостого хода трансформатора ΔР_x , которые приводятся в его паспортных данных.

Потери реактивной мощности в стали определяются по току холостого хода трансформатора, значение которого в процентах приводится в его паспортных данных.

Потери мощности в обмотках трансформатора можно определить двумя путями:

• по параметрам схемы замещения;
• по паспортным данным трансформатора.

Потери мощности по параметрам схемы замещения определяются по тем же формулам, что и для ЛЭП:

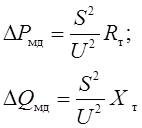
где S – мощность нагрузки;
U – линейное напряжение на вторичной стороне трансформатора.

Для трехобмоточного трансформатора или автотрансформатора потери в меди определяются как сумма потерь мощности каждой из обмоток. Полные потери мощности в двухобмоточном трансформаторе равны:

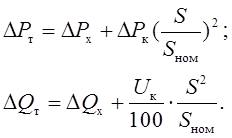
Если на подстанции с суммарной нагрузкой S работает параллельно n одинаковых трансформаторов, то их эквивалентные сопротивления в n раз меньше, а проводимости в n раз больше.

4. Недетерминированная модель электрической нагрузки

Недетерминированный характер изменения электрической нагрузки в реальных электрических сетях обусловлен наличием большого количества разнотипных электроприёмников [5]. При передаче электроэнергии по участку электрической сети возникают потери мощности, которые в общем случае не являются детерминированной величиной. В работе решается задача статистического моделирования потерь мощности на участке электрической сети при недетерминированной мощности нагрузки.

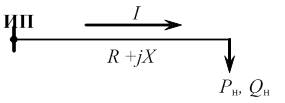
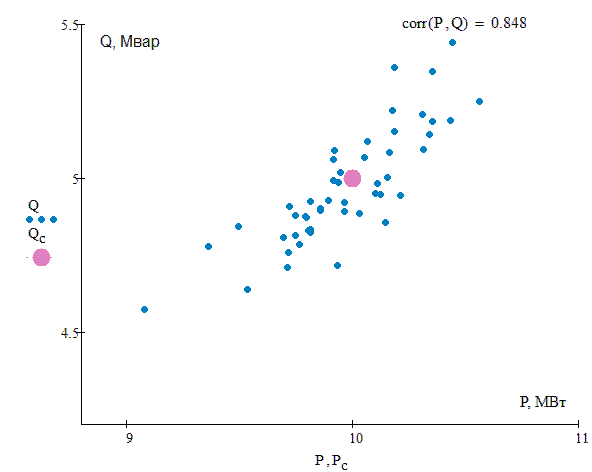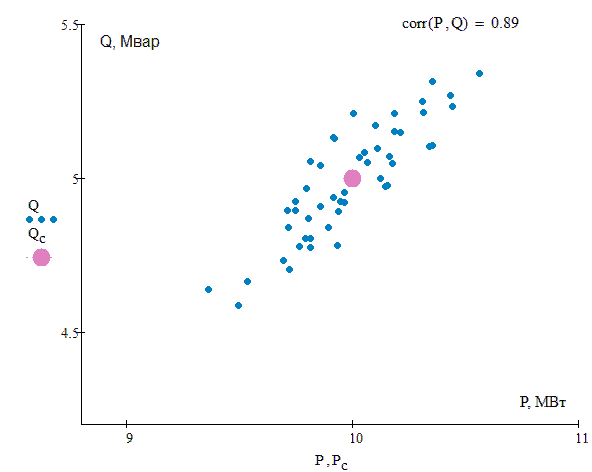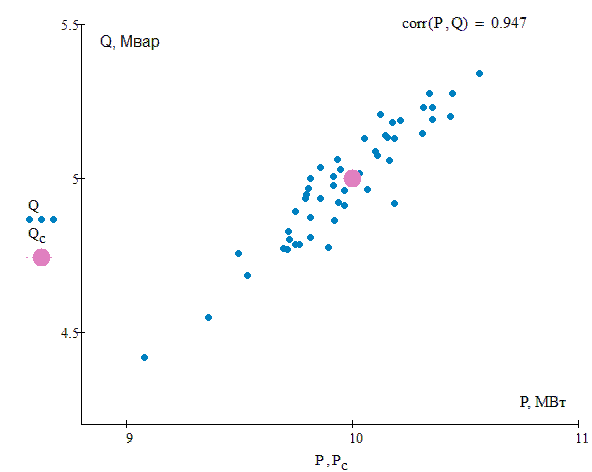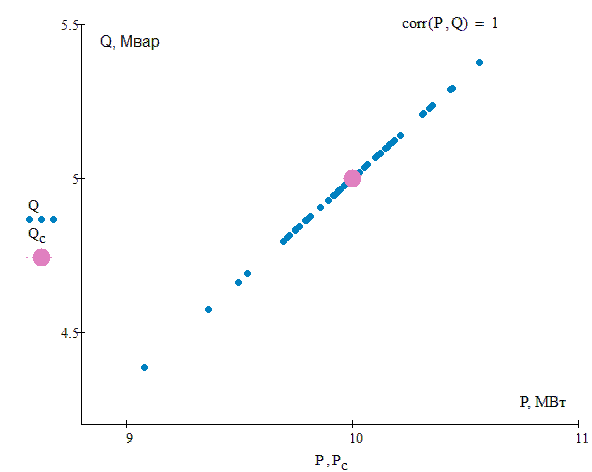
Рассматривается вероятностная модель электрической нагрузки, которая задается как система случайных коррелированных величин активной Р и реактивной Q мощностей [6-7], подчиненных нормальному закону распределения. Для системы случайных величин (P , Q) характеристиками являются средние значения Рc, Qc, среднеквадратические отклонения σ_P, σ_Q и коэффициент корреляции r_PQ, (рис.2). Параметры сети рассматриваются как детерминированные величины. Для статистического моделирования используется метод Монте-Карло [8].

Рисунок 2 – Cистема случайных коррелированных величин активной и реактивной мощности при различной величине коэффициента корреляции (анимация: 16 кадров; 33,7 Кб)

5. Мероприятия по снижению потерь мощности

Потери мощности и электроэнергии достигают значительных величин и являются одним из основных фактов, влияющих на экономичность сетей. Их величина регламентируется постановлениями регулирующих органов в сетях напряжением до 35 кВ и в сетях напряжениям 35 кВ и выше.

Большая часть потерь электроэнергии (60 – 70%) приходится на сети напряжением 6 – 10 кВ [9]. Поэтому перечисленные ниже мероприятия относятся к сетям этих напряжений и к электроприемникам:

• применение более высокой ступени напряжения (10 кВ вместо 6 кВ);
• повышение уровня напряжения в сети путем применения устройств регулирования напряжения;
• регулирование потоков активной и реактивной мощностей в отдельных звеньях сети;
• применение рациональных схем питания потребителей, которые позволяют осуществлять более экономичную загрузку ЛЭП и трансформаторов;
• рационализация энергохозяйств предприятий – улучшение cosφ, правильный выбор мощности и загрузка электродвигателей.

6. Расчет потерь электроэнергии

При передаче электроэнергии часть ее расходуется на нагрев, создание электромагнитных полей и другие эффекты. Этот расход принято называть потерями. В электроэнергетике термин потери имеет специфическое значение. Если в других производствах потери связаны с браком продукции, то потери электроэнергии – это технологический расход на ее передачу.

Величина потерь электроэнергии зависит от характера изменения нагрузки в рассматриваемый период времени. Например, в ЛЭП, работающей с неизменной нагрузкой, потери электроэнергии за время t рассчитываются следующим образом:

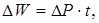
где ΔP ‒ суммарные потери активной мощности в сопротивлении и проводимости ЛЭП.

Если нагрузка меняется, то потери электроэнергии можно рассчитать различными способами. В зависимости от используемой математической модели методы делятся на две групп:

• детерминированные;
• вероятностно-статистические.

Наиболее точным из детерминированных методов является метод расчета потерь электроэнергии по графику нагрузок для каждого потребителя.

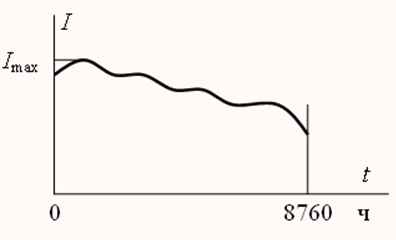
Предположим, что нагрузка потребителя в году менялась по следующему графику (рис.3). Тогда справедливы формулы

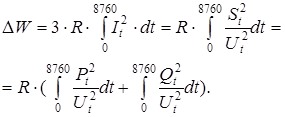
Интеграл – это фактически площадь, ограниченная графиком изменения квадрата тока. Таким образом, потери активной электроэнергии пропорциональны площади квадратичного годового графика нагрузки.

Рисунок 3 – График нагрузки потребителя

7. Задача расчета режимов. Основные допущения

Задача расчета режима заключается в определении параметров режима, к которым относятся [10]:

• значения токов в элементах сети;
• значения напряжений в узлах сети;
• значения мощностей в начале и конце элемента сети;
• значения потерь мощности и электроэнергии.

Расчет этих величин необходим для выбора оборудования, обеспечения качества электроэнергии, оптимизации режимов работы сетей. Исходными данными для расчета режима являются:

• схема электрических соединений и ее параметры – значения сопротивлений и проводимостей ее элементов;
• мощности нагрузок или их графики мощности;
• значения напряжений в отдельных точках сети.

Теоретически сеть можно рассчитать с помощью методов, известных в ТОЭ, основанные на законах Кирхгофа. Однако, непосредственное их применение затруднено по двум причинам:

• большое количество элементов в реальной сети;
• специфика задания исходных данных.

Специфика задания исходных данных заключается в следующем – задаются мощности нагрузок и напряжение на источнике питания. Для того, чтобы построить картину потокораспределения, т.е. найти значения мощностей в конце и начале каждого элемента, нужно вычислить потери мощности. Для их вычисления необходимо знать ток в каждом элементе. Его значение можно вычислить при известном напряжении на шинах нагрузки. А оно в начале расчета неизвестно. Поэтому применять законы Кирхгофа непосредственно для получения однозначного решения невозможно.

Основным методом расчета режимов электрических сетей является метод последовательных приближений – итерационный метод. Он заключается в том, что в начале расчета задаются первым приближением напряжений в узлах (нулевая итерация). Обычно за нулевую итерацию принимают допущение о том, что напряжения во всех узлах схемы равны между собой и равны номинальному значению сети. По принятому значению напряжения и заданной мощности потребителей можно рассчитать значения параметров режима, в том числе и значения напряжения в узлах сети. Эти значения напряжения будут вторым приближением (первой итерацией). Расчет повторяют до тех пор, пока результаты последующих приближений не будут отличаться друг от друга с заданной точностью.

Чаще всего достаточно 1-2 итераций. Если же решаются задачи оптимизации режима, связанные с потерями мощности, то нужно много итераций.

Возможность малого количества итераций привела к появлению нестрогих, но дающих приемлемые результаты, методов. Такими являются:

• метод расчета режима при заданном напряжении в конце ЛЭП;
• метод расчета режима при заданном напряжении в начале ЛЭП (на источнике питания).

При расчете сетей напряжением до 35 кВ включительно принимаются следующие допущения:

• не учитывается зарядная мощность ЛЭП;
• не учитывается индуктивное сопротивление кабельных ЛЭП;
• не учитываются потери мощности в стали трансформаторов. Потери мощности в стали трансформаторов учитываются лишь при подсчете потерь активной мощности и электроэнергии во всей сети;
• при расчете потоков мощности не учитываются потери мощности, т.е . мощность в начале участка равна мощности в конце участка;
• не учитывается поперечная составляющая падения напряжения. Это значит, что не учитывается сдвиг напряжения по фазе между узлами схемы;
• расчет потерь напряжения ведется по номинальному напряжению, а не по реальному напряжению в узлах сети.

8. Баланс мощностей в энергосистеме

Передача электроэнергии по ЛЭП электромагнитными волнами осуществляется со скоростью, близкой к скорости света, т.е. практически мгновенно. Это приводит к тому, что производство, распределение и потребление электроэнергии происходит одновременно [11]. Поэтому в любой момент времени установившегося режима системы должны вырабатывать мощность, равную мощности потребителей и потерям мощности в элементах системы. Другими словами, в энергосистеме должен иметь баланс выдаваемой и потребляемой мощности:

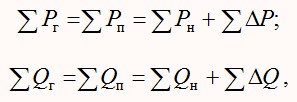
Потери активной мощности включают в себя потери мощности в воздушных и кабельных ЛЭП, электромагнитных аппаратов и устройств управления режимами системы.

Суммарные потери реактивной мощности – это алгебраическая сумма потерь мощности в сопротивлениях и проводимостях воздушных и кабельных ЛЭП, трансформаторах, мощности намагничивания и рассеяния электромагнитных аппаратов.

При неизменном составе нагрузок активная и реактивная мощность, потребляемая системой, является функцией частоты и напряжения на шинах потребителей. Баланс мощности в системе отвечает некоторым определенным значениям частоты и напряжения.

Количественную оценку изменения величин, входящих в уравнение баланса, можно выполнить по статическим характеристикам нагрузки (потребителей) P_п и Q_п.

Из анализа баланса мощностей в энергосистеме следует, что для регулирования напряжения нужно воздействовать, в первую очередь, на реактивную мощность, а для регулирования частоты нужно изменять активную мощность.

Поэтому в задачу регулирования режима входят подразделы:

• регулирование активной мощности и частоты в энергосистеме;
• регулирование реактивной мощности и напряжения в энергосистеме.

Такое разделение объясняется и физикой процесса производства электроэнергии. Частота тока определяется частотой вращения синхронных машин, которая зависит от соотношения вращающего и тормозного моментов на валу агрегата турбина-генератор. Для изменения их соотношения нужно изменить (увеличить или уменьшить) впуск энергоносителя в турбину. При этом изменяется выработка активной мощности, частота вращения синхронных машин и, как следствие, частота тока в энергосистеме.

Кроме того следует учитывать, что

• к изменению частоты в энергосистеме предъявляются более жесткие требования, чем к изменению напряжения;
• для каждой электростанции задается оптимальный график работы;
• кроме генераторов существуют дополнительные источники реактивной мощности, которые можно устанавливать в местах более близких к потребителям.

Список источников

1. Идельчик, В. И. Электрические системы и сети: Учебник для вузов. / В.И. Идельчик. ‒ М.: Энергоатомиздат, 1989, — 592 с: ил.
2. Глазунов, А.А. Электрические сети и системы 4-е изд., перераб. и доп. / А.А. Глазунов. ‒ М.: Госэнергоиздат, 1960. ‒ 368 с.
3. Лыкин, А.В. Электрические системы и сети : учебник / А.В. Лыкин. — Новосибирск : Новосибирский государственный технический университет, 2017. — 363 c.
4. Потери энергии в электрических сетях и установках : учебное пособие / Г. В. Маслакова, А. А. Митрофанов, Е. А. Чащин, Ю. А. Шурыгин. — Липецк : Липецкий государственный технический университет, ЭБС АСВ, 2018. — 79 c.
5. Электрические нагрузки промышленных предприятий / С.Д. Волобринский, Г.М. Каялов, П.Н. Клейн, Б.С. Мешель. − Л.: Энергия, 1971. − 264 с.
6. Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. – М. : Наука, 1965. – 576 с.
7. Аркашов, Н.С. Теория вероятностей и случайные процессы : учебное пособие / Н. С. Аркашов, А. П. Ковалевский. — 2-е изд. — Новосибирск : Новосибирский государственный технический университет, 2017. — 238 c.
8. Метод статистических испытаний (метод Монте-Карло) / Н. П. Бусленко, Д. И. Голенко, И. М. Соболь и др.; под ред. Ю. А. Шрейдера. – М.: Физматгиз, 1962. – 331 с.
9. Лыкин, А.В. Распределительные электрические сети : учебное пособие / А.В. Лыкин. — Новосибирск : Новосибирский государственный технический университет, 2018. — 115 c.
10. Лыков, Ю.Ф. Расчеты систем электроснабжения : сборник задач и упражнений / Лыков Ю.Ф. — Самара : Самарский государственный технический университет, ЭБС АСВ, 2018. — 54 c.
11. Стрельников, Н. А. Энергосбережение : учебное пособие / Н. А. Стрельников. — Новосибирск : Новосибирский государственный технический университет, 2019. — 72 c.