Реферат по теме выпускной работы
Внимание! На момент написания данного реферата магистерская работа не завершена. Предполагаемая дата завершения – май 2024 г. Полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Содержание
- Введение
- 1. Цель и задачи исследования, планируемые результаты
- 2. Основные понятия и методы многомерной статистики
- 2.1 Факторный анализ
- 2.2 Дискриминантный анализ
- 2.3 Кластерный анализ
- 2.4 Многомерное масштабирование
- 2.5 Методы контроля качества
- 3. Применение многомерного статистического анализа в региональных исследованиях
- 4. Применение методов математической статистики для анализа демографической ситуации в ДНР
- Выводы
- Список источников
Введение
Одним из ключевых аспектов развития современных государств является эффективное управление территориальным развитием. В условиях постоянно меняющейся экономической, социальной и политической обстановки возникает необходимость в проведении многомерного математико-статистического анализа развития регионов с целью выявления основных тенденций, закономерностей и определения приоритетных направлений развития.
Многомерный математико-статистический анализ представляет собой совокупность методов и инструментов, позволяющих исследовать взаимосвязь между различными факторами, влияющими на развитие региона, и определить степень их влияния на ключевые показатели. Это позволяет выявить наиболее перспективные регионы и разработать стратегии их развития, а также определить приоритетные направления для привлечения инвестиций и улучшения качества жизни населения.
1. Цель и задачи исследования, планируемые результаты
Целью данного исследования является проведение многомерного математико-статистического анализа развития регионов для определения основных тенденций и закономерностей, а также разработки рекомендаций по оптимизации управления территориальным развитием и улучшению качества жизни населения на региональном уровне.
2. Основные понятия и методы многомерной статистики
Бывают ситуации, в которых случайная изменчивость была представлена одной или двумя случайными величинами, признаками. Например, при изучении статистической совокупности людей нас интересуют рост и вес. В этой ситуации, независимо от того, сколько людей входит в статистическую совокупность, мы всегда можем составить точечную диаграмму и увидеть картину в целом. Но если, например, есть три признака, добавляется признак — возраст человека, то диаграмма рассеяния должна быть составлена в трехмерном пространстве. Уже довольно сложно представить набор точек в трехмерном пространстве.
Фактически, на практике не каждое наблюдение представлено одним, двумя или тремя числами, а некоторым видимым набором чисел, которые описывают десятки символов. В этой ситуации для составления диаграммы рассеяния необходимо было бы рассмотреть многомерные пространства. Раздел статистики, посвященный исследованиям экспериментов с многомерными наблюдениями, называется многомерным статистическим анализом [1].
Измерение сразу нескольких признаков (свойств объекта) в одном эксперименте в общем более естественно, чем измерение какого-либо одного, двух. Поэтому потенциально многомерный статистический анализ имеет широкое поле для применения.
К многомерному статистическому анализу относят следующие разделы:
- факторный анализ;
- дискриминантный анализ;
- кластерный анализ;
- многомерное шкалирование;
- методы контроля качества.
2.1 Факторный анализ
В современной статистике этот метод анализа данных используется для выявления скрытых факторов, влияющих на наблюдаемые переменные. Основная идея факторного анализа заключается в том, что многие переменные могут быть сведены к меньшему числу факторов, которые объясняют основные тенденции и взаимосвязи между этими переменными.
Факторный анализ может применяться во многих областях, от экономики и бизнеса до медицинской и психологической статистики. Этот метод помогает исследователям определить, какие факторы влияют на наблюдаемые переменные и какие переменные наиболее чувствительны к воздействию этих факторов.
Одной из важнейших задач, которая может быть решена с помощью факторного анализа, является выявление основных факторов, влияющих на изменение показателей в пределах определенной выборки. Кроме того, факторный анализ может быть использован для определения взаимосвязей между различными переменными, а также для прогнозирования значений этих переменных, на основе имеющихся данных [2].
В целом факторный анализ является мощным инструментом, который позволяет исследователям более глубоко и точно изучать взаимосвязи между различными переменными, выявлять скрытые факторы и создавать более точные модели для прогнозирования будущих значений этих переменных.
Основная идея факторного анализа заключается в выявлении наиболее важных и значимых факторов в наборе переменных, обладающих сходными характеристиками.
Чтобы понять факторный анализ, необходимо знать основные понятия и определения, которые являются частью его теоретического аппарата. Наиболее важными из них являются понятия фактор, факторная нагрузка, полезность, внутренняя ценность, факторное пространство.
Фактор - это своего рода скрытая переменная, объясняющая взаимосвязь между набором переменных. Факторы могут быть разными, например, в медицинской статистике в качестве факторов могут выступать болезни, в экономике – параметры экономической активности, а в социологии – социальные факты. С помощью факторного анализа можно выявить наиболее значимые факторы, которые имеют наибольшую корреляцию с набором данных и объясняют наибольшую часть вариабельности.
Факторная нагрузка – это коэффициент, который показывает, насколько сильно каждый показатель влияет на данный фактор. Факторная нагрузка может быть положительной или отрицательной, что указывает на направление влияния. Чем выше факторная нагрузка, тем большую роль играет конкретный показатель в формировании данного фактора.
Коммунальность – это коэффициент, который показывает, насколько отдельный показатель объясняется общим фактором. Коммунальность близка к единице, если переменная является хорошим представителем данного фактора. Чем ближе коммунальность к нулю, тем слабее связь данной переменной с общим фактором [3].
Собственное число – это значение, которое отражает, насколько важный фактор можно выделить из набора данных. Собственное число рассчитывается на основе собственных векторов, и чем выше это число, тем важнее соответствующий фактор.
Факторное пространство – это многомерное пространство, в котором каждая переменная представлена фактором. Факторное пространство показывает, насколько сильна корреляция между различными показателями, и позволяет увидеть, какие переменные находятся ближе друг к другу и какие – дальше.
Принцип работы факторного анализа заключается в том, что анализируется матрица данных, где каждый столбец представляет собой переменную, а каждая строка – наблюдение.
В рамках факторного анализа, переменные группируются по сходству и факторизуются, то есть разделяются на основу общих свойств, которые присутствуют в их корреляционной структуре. С помощью факторного анализа можно выявлять зависимости между переменными и определять, какие из них наиболее значимы, а какие не влияют на общую картину.
Результатами факторного анализа могут быть главные компоненты, которые представляют собой комбинацию исходных переменных, а также их весовые коэффициенты. Основная цель факторного анализа – уменьшить количество переменных, минимизировать пересечения между ними и выявить настоящие отличительные признаки набора данных.
2.2 Дискриминантный анализ
Пусть имеется совокупность объектов, разбитая на несколько групп, и для каждого объекта можно определить, к какой группе он относится. Для каждого объекта имеются измерения нескольких количественных характеристик. Необходимо найти способ, как на основании этих характеристик можно узнать группу, к которой относится объект. Это позволит указывать группы, к которым относятся новые объекты той же совокупности. Для решения поставленной задачи применяются методы дискриминантного анализа.
Дискриминантный анализ — это раздел статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам.
Дискриминантный анализ оказывается удобным при обработке результатов тестирования отдельных лиц, когда дело касается приема на ту или иную должность. В этом случае необходимо всех кандидатов разделить на две группы: «подходит» и «не подходит» [4].
Использование дискриминантного анализа возможно банковской администрацией для оценки финансового состояния дел клиентов при выдаче им кредита. Банк по ряду признаков классифицирует их на надежных и ненадежных.
Дискриминантный анализ может быть привлечен в качестве метода разбиения совокупности предприятий на несколько однородных групп по значениям каких-либо показателей производственно-хозяйственной деятельности.
Методы дискриминантного анализа позволяют строить функции измеряемых характеристик, значения которых и объясняют разбиение объектов на группы. Желательно, чтобы этих функций (дискриминантных признаков) было немного. В этом случае результаты анализа легче содержательно толковать.
Благодаря своей простоте особую роль играет линейный дискриминантный анализ, в котором классифицирующие признаки выбираются как линейные функции от первичных признаков.
2.3 Кластерный анализ
Методы кластерного анализа позволяют разбить изучаемую совокупность объектов на группы «схожих» объектов, называемых кластерами. Слово кластер английского происхождения — cluster переводится как кисть, пучок, группа, рой, скопление.
Кластерный анализ решает следующие задачи:
- Проводит классификацию объектов с учетом всех тех признаков, которые характеризуют объект. Сама возможность классификации продвигает нас к более углубленному пониманию рассматриваемой совокупности и объектов, входящих в нее.
- Ставит задачу проверки наличия априорно заданной структуры или классификации в имеющейся совокупности. Такая проверка дает возможность воспользоваться стандартной гипотетико-дедуктивной схемой научных исследований.
Большинство методов кластеризации (иерархической группы) являются агломеративными (объединительными) — они начинают с создания элементарных кластеров, каждый из которых состоит ровно из одного исходного наблюдения (одной точки), а на каждом последующем шаге происходит объединение двух наиболее близких кластеров в один [5].
Момент остановки этого процесса может задаваться исследователем (например, указанием требуемого числа кластеров или максимального рассто¬яния, при котором достигнуто объединение).Графическое изображение процесса объединения кластеров может быть получено с помощью дендрограммы — дерева объединения кластеров.
2.4 Многомерное масштабирование
Многомерное масштабирование (MDS) - это статистический метод, который используется для анализа и визуализации данных на основе сравнительных оценок или сходств между объектами. Он позволяет представлять многомерные данные в виде геометрической структуры в пространстве меньших размеров.
Основная идея метода многомерного масштабирования заключается в поиске отображения (преобразования), сохраняющего относительные расстояния или сходства между объектами. Таким образом, больше похожих объектов будет расположено ближе друг к другу, а меньше похожих объектов будет расположено дальше друг от друга. Метод многомерного шкалирования может быть использован для различных типов данных, таких как оценки сходства между продуктами, оценки предпочтений потребителей, результаты психологических тестов и т.д. Он широко используется в различных областях, включая маркетинг, социологию, психологию, биологию и другие [6].
Основной принцип метода многомерного шкалирования заключается в сохранении относительных расстояний между объектами. Это означает, что если два объекта более похожи друг на друга, то они должны быть расположены ближе друг к другу, чем объекты, которые менее похожи. Таким образом, метод стремится сохранить структуру исходных данных в пространстве меньшей размерности.
2.5 Методы контроля качества
Методы контроля качества предназначены для контроля качества выпускаемой продукции с целью выявления нарушений и «узких мест» в организации производства и в технологических процессах. Повсеместное применение научно обоснованных методов контроля качества явилось немаловажным фактором успехов стран-лидеров мировой экономики, в особенности Японии.
В последнее время новые методы более эффективного управления с целью повышения качества получили название «шесть сигм». Они рассматриваются как формула успеха большинства транснациональных корпораций [7]. В отличие от большинства описанных выше методов многомерного анализа методы контроля качества не требуют трудоемких вычислений — они исключительно просты и наглядны. Простота, наглядность и эффективность статистических методов контроля качества сделали возможным и оправданным их повсеместное применение в передовых странах, вплоть до мастеров, а иногда и отдельных рабочих.
3. Применение многомерного статистического анализа в региональных исследованиях
Многомерный статистический анализ применяется в региональных исследованиях для изучения взаимосвязи различных факторов, влияющих на развитие региона. Например, можно изучить взаимосвязь между уровнем экономического развития региона и уровнем образования населения, между уровнем безработицы и уровнем преступности, между уровнем инвестиций и уровнем развития инфраструктуры и т.д.
Также многомерный статистический анализ может использоваться для классификации регионов по различным признакам, таким как уровень экономического развития, уровень социальной напряженности, уровень экологической безопасности и т.д. Это позволяет определить наиболее проблемные регионы и разработать меры по их поддержке и развитию.
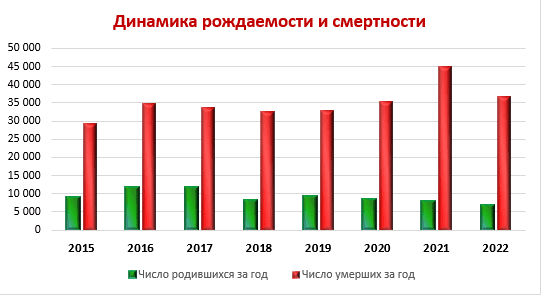
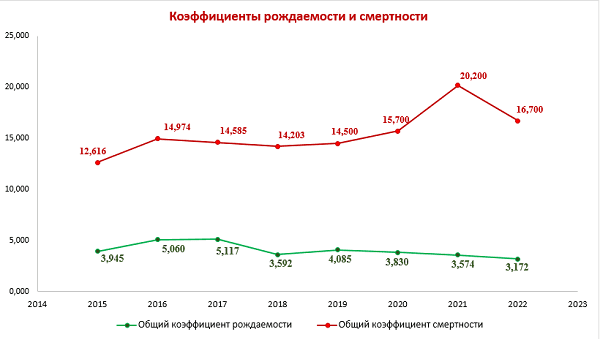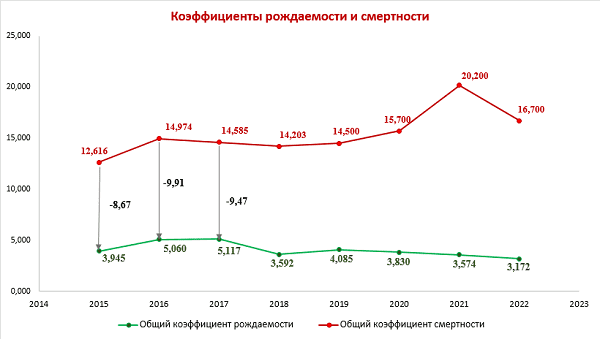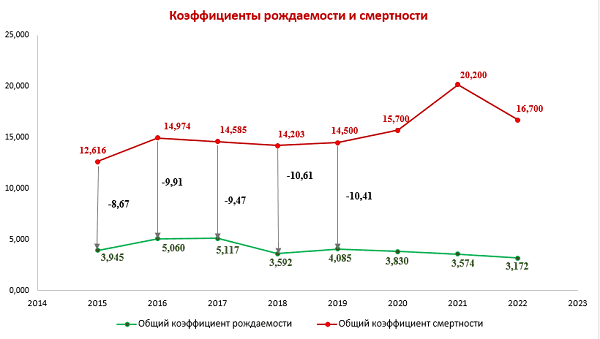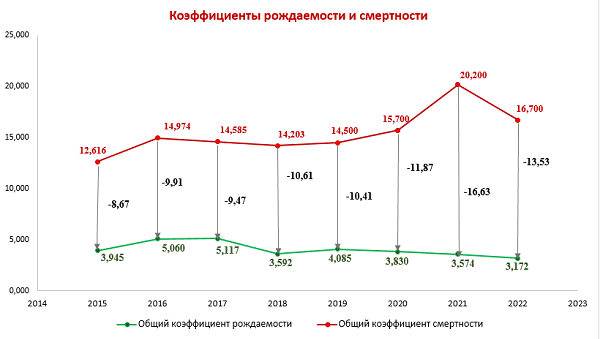
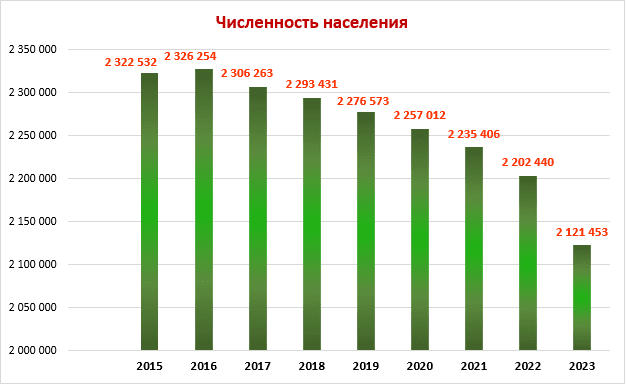
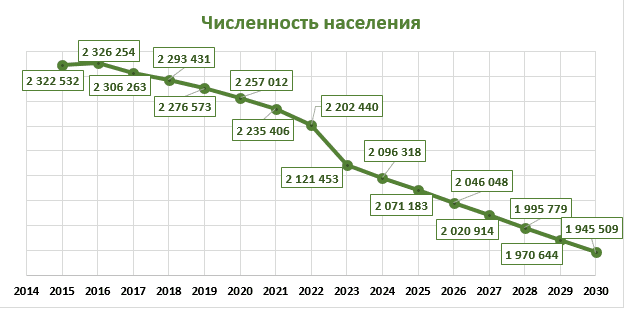
4. Применение методов математической статистики для анализа демографической ситуации в ДНР
Самыми важными показателями общественного здоровья любой страны являются демографические показатели, которые характеризуют стабильность и безопасность, а также перспективы ее дальнейшего развития.
В этом контексте, анализ демографической ситуации с использованием методов математической статистики становится особенно актуальным. Ведь именно такой подход позволяет получить наиболее точные и объективные данные о состоянии населения, его структуре и динамике изменений.
Одним из ключевых инструментов математической статистики является анализ временных рядов, который позволяет выявить тенденции и закономерности в изменении демографических показателей. Также используются методы моделирования и прогнозирования, позволяющие предсказать возможные сценарии развития демографической ситуации [8-10].
В целом, применение методов математической статистики позволяет получить более глубокое понимание демографических процессов и принимать обоснованные решения в области социальной политики, здравоохранения и других сферах, связанных с общественным здоровьем и благополучием населения.