Реферат по теме выпускной работы
Содержание
- Введение
- 1. Основные положения теории оптимизации
- 2. Классификация задач оптимизации
- 3. Классификация методов оптимизации
- Заключение
- Список использованных источников
Введение
В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов Х [1]. Важность и ценность теории оптимизации заключается в том, что она дает адекватные понятийные рамки для анализа и решения многочисленных задач: в исследовании операций:
- задачи оптимального планирования деятельности предприятий (управления);
- задачи оптимального прикрепления потребителей к поставщикам (транспортная);
- задачи оптимального распределения трудовых ресурсов;
- задача оптимального составления смесей;
- бинарные задачи распределения;
- задачи о раскрое;
- задачи формирования оптимального портфеля ценных бумаг (инвестиционных проектов)
- в численном анализе: аппроксимация, регрессия, решение линейных и нелинейных систем, численные методы, включая методы конечных элементов и т. д.;
- в автоматике: распознавание образов, оптимальное управление, фильтрация, управление производством, робототехника и т. д.;
- в математической экономике: решение больших макроэкономических моделей, моделей предпринимательства, теория принятия решений и теория игр.
Постановка каждой задачи оптимизации (ЗО) включает в себя два объекта: множество допустимых решений и целевую функцию (функционал), которую следует минимизировать или максимизировать на указанном множеств [2]. С этой общей точки зрения и рассматриваются различные классы экстремальных задач, составляющие предмет линейного, нелинейного, динамического программирования, вариационного исчисления и теории оптимального управления [3].
Первые работы по экстремальным задачам при наличии ограничений общего вида (в виде равенств и неравенств) относятся к концу 30-х — началу 40-х годов ХХ века. Здесь необходимо упомянуть имена американских ученых Чикагской школы, таких как Г. Блисс, О. Больц, Е. Макшейн, Л. М. Грейвс и др. Независимо от исследований американских ученых оптимизационная тематика развивалась и в СССР [4]. Пионером в этой области был Л. В. Канторович, опубликовавший в 1939 г. книгу, содержавшую математические постановки ряда экономических задач. Но работы Канторовича, как и результаты американских ученых, не привлекли внимание математиков и остались, по существу, незамеченными [5].
Время для этих задач созрело несколько позже: в конце 40-х годов прошлого века. Под влиянием прикладной тематики, которой приходилось заниматься в годы второй мировой войны (проблема снабжения военных плацдармов войск второго фронта в Европе и Африке), Данциг в США стал изучать задачи минимизации при линейных ограничениях, получившие название задач линейного программирования (ЗЛП). Под влиянием работ фон Неймана по теории игр, Данциг, Гейл, Кун и Таккер создали теорию двойственности в ЛП — специфическую формулировку условий существования extr.
1. Основные положения теории оптимизации
Математическая теория оптимизации включает в себя фундаментальные результаты и численные методы, позволяющие находить наилучший вариант из множества возможных альтернатив без их полного перебора и сравнения [6]. Для того чтобы использовать результаты и вычислительные процедуры теории оптимизации на практике, необходимо, прежде всего, сформулировать рассматриваемую задачу на математическом языке, т. е. построить математическую модель объекта оптимизации.
В большинстве реальных ситуаций дать исчерпывающее математическое представление оптимизируемой системы с учетом всех взаимосвязей ее частей, взаимодействий с внешним миром, всех целей ее функционирования бывает затруднительно или вовсе невозможно [7]. При построении математической модели необходимо, как правило, выделять и учитывать в дальнейшем только наиболее важные, существенные стороны исследуемого объекта с тем, чтобы было возможным его математическое описание, а также последующее решение поставленной задачи. При этом неучтенные в математической модели факторы не должны существенно влиять на окончательный результат оптимизации [8]. Поэтому процесс построения математической модели для решения оптимизационной задачи можно разбить на следующие основные этапы:
1) Определение границ объекта оптимизации.
Необходимость этого этапа диктуется невозможностью учета и исчерпывающего описания всех сторон большинства реальных систем. Выделив главные переменные, параметры и ограничения, следует приближенно представить систему как некоторую изолированную часть реального мира и упростить ее внутреннюю структуру [9].
2) Выбор управляемых переменных.
На этом этапе построения математической модели необходимо провести различие между теми величинами, значения которых можно выбирать и варьировать с целью достижения наилучшего результата (управляемыми переменными), и величинами, которые фиксированы или определяются внешними факторами [10].
3) Определение ограничений на управляемые переменные.
В реальных условиях на выбор значений управляемых переменных, как правило, наложены ограничения, связанные с ограниченностью имеющихся ресурсов, мощностей и других возможностей. При построении математической модели эти ограничения обычно записывают в виде равенств и неравенств или указывают множества, которым должны принадлежать значения управляемых переменных [11].
4) Выбор числового критерия оптимизации.
Обязательной составной частью математической модели объекта оптимизации является числовой критерий, минимальному или максимальному значению которого (в зависимости от конкретной задачи) соответствует наилучший вариант поведения исследуемого объекта [11].
5) Формулировка математической задачи оптимизации.
Объединяя результаты предыдущих этапов построения математической модели, ее записывают в виде математической задачи оптимизации, включающей построенную целевую функцию и найденные ограничения на управляемые переменные. В общем виде математическую задачу оптимизации можно сформулировать следующим образом: минимизировать (максимизировать) целевую функцию с учетом ограничений на управляемые переменные [13].
Под минимизацией (максимизацией) функции n переменных f(х) = f(xl, ..., хn) на заданном множестве Un-мерного векторного пространства En понимается определение хотя бы одной из точек минимума (максимума) этой функции на множестве U, а также, если это необходимо, и минимального (максимального) на U значения f(x).
2. Классификация задач оптимизации
Многие задачи оптимизации сводятся к отысканию наименьшего, (или наибольшего), значения целевой функции или показателя качества. В зависимости от вида целевой функции и вида ограничений на область и параметры функции различают несколько типов задач оптимизации.
Выделение и подробное рассмотрение одномерных задач имеет определенный смысл. Эти задачи наиболее просты, на них легче понять постановку вопроса, методы решения и возникающие трудности. В ряде случаев, хотя и очень редко, одномерные задачи имеют самостоятельный практический интерес. Однако самое главное заключается в том, что алгоритмы решения многомерных задач оптимизации часто сводятся к последовательному многократному решению одномерных задач [14].
Однако подавляющее число реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем иногда их число может быть весьма большим.
Математическая постановка таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции f(x), заданной на некотором множестве En возможных значений ее аргументов. При этом целевая функция должна быть непрерывной, а множество En — представлять собой замкнутую ограниченную область [15].
Многие практические задачи оптимизации сводятся к математическим моделям вида:
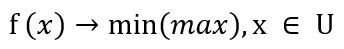
где допустимое множество U не совпадает со всем пространством En.
В этих случаях говорят об условной минимизации функции n переменных.
В большинстве случаев допустимое множество U определяется ограничениями – равенствами и (или) неравенствами, т. e. рассматривается задача:
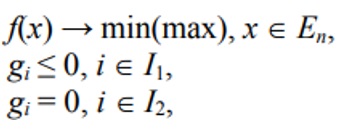
где I1, I2 є [1, …, m] — заданные множества индексов.
Такая постановка задачи представляет собой запись условий так называемой задачи математического программирования. Различают несколько частных видов задачи математического программирования [16]:
1) задача линейного программирования — когда целевая функция и все ограничения линейны, а переменные хj удовлетворяют условию неотрицательности хj >= 0;
2) задача нелинейного программирования — когда хотя бы одна их функций f(x), gi(х) не является линейной;
3) задача на условный экстремум — отсутствуют ограничения неравенства, т.е. I1 = 0;
4) задача выпуклого программирования — все функции f(x), gi(х) выпуклы, а ограничения в виде равенств отсутствуют, то есть I2 = 0. Ее допустимое множество U — выпукло.
Широкий класс дискретных задач оптимизации составляют целочисленные задачи математического программирования. Такие задачи возникают, когда управляемые переменные хi по своему смыслу могут принимать только целочисленные значения (например, хi — это количество единиц используемого оборудования или число резервных блоков в схеме электронного устройства и т. п.).
Еще одним примером математической модели дискретной задачи оптимизации является задача о выборе кратчайшего пути в ориентированном графе.
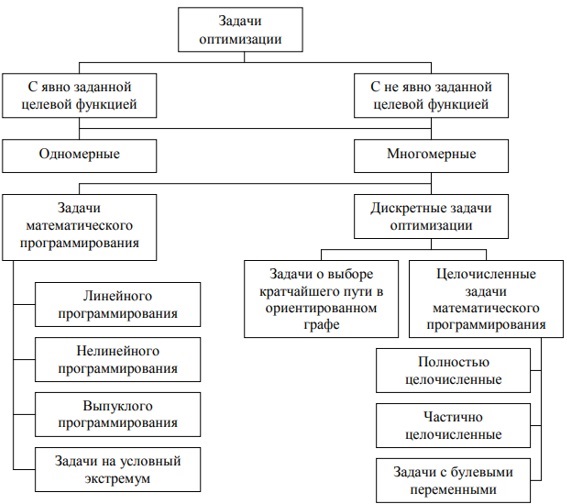
К формальной схеме поиска кратчайшего пути в ориентированном графе сводятся прикладные задачи оптимизации различного содержания. Эти задачи объединяют возможность представить процесс поиска оптимального решения в виде последовательности принятых частичных решений о выборе одного варианта из нескольких возможных. Принятию каждого из этих частичных решений соответствует выбор одной из дуг, исходящих из некоторой вершины графа, а вес выбранной дуги характеризует «качество» принятого частичного решения. Обобщая вышеизложенное, классификацию задачи оптимизации можно представить следующим образом (рисунок 2.1) [17].
3. Классификация методов оптимизации
Для каждого класса оптимизационных задач существуют различные (чаще всего специфические) методы их решения. Рассмотрим классификацию основных из этих методов.
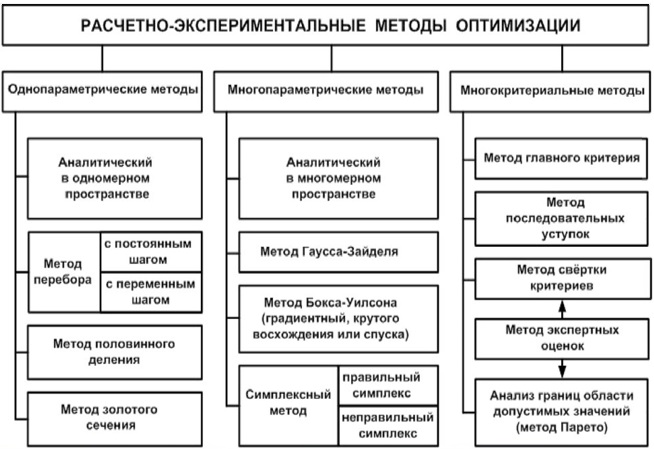
Рисунок 3.1 — Классификация методов оптимизации
Классификация методов оптимизации может быть выполнена следующим образом:
1) По размерности решаемой задачи: одномерные и многомерные.
2) По способу формирования шага многомерные методы делятся на следующие виды:
- градиентные;
- безградиентные;
- случайного поиска.
В свою очередь, градиентные методы можно классифицировать:
- по алгоритму коррекции шага;
- по алгоритму вычисления новой точки (одношаговые и многошаговые).
Безградиентные методы делятся на методы: с поочередным изменением переменных и с одновременным изменением переменных.
Методы случайного поиска делятся на методы с чисто случайной стратегией и со смешанной стратегией.
3) По наличию активных ограничений методы оптимизации можно разделить:
- без ограничений (безусловные);
- с ограничениями (условные).
В свою очередь, последние могут быть:
- с ограничениями типа равенства;
- ограничениями типа неравенств;
- смешанные.
К методам одномерной оптимизации, то есть методам решения задач оптимизации вида f(х) => min(max), а < х < b, где х — скаляр, а и b — соответственно минимальное и максимальное возможные значения переменной х относятся следующие методы:
- метод сканирования. Достоинство метода состоит, в том, что можно найти глобальный максимум критерия, если f(x) — многоэкстремальная функция.
- метод деления пополам. К недостаткам метода относится его работоспособность только для одноэкстремальных функций (т. е. таких, которые содержат один экстремум того типа, который мы ищем в задаче), так как в других случаях при сравнении двух критериев в соседних точках невозможно правильно выбрать следующий интервал, где находится экстремум;
- метод золотого сечения. Метод обеспечивает более быструю сходимость к решению, чем многие другие методы, и применим, очевидно, только для одноэкстремальных функций;
- метод параболической аппроксимации. К достоинству метода относится высокая скорость сходимости к оптимуму, хотя метод может не всегда сходиться к нему [18].
Рассмотрим методы многомерной безусловной градиентной оптимизации.
К методам многомерной безусловной градиентной, оптимизации относятся [19]:
- метод градиента. Основной недостаток метода — необходимость частого вычисления производных от f(х);
- метод наискорейшего спуска (лишен недостатка предыдущего метода, однако, как и все градиентные методы, обладает невысокой эффективностью в овражных функциях);
- метод сопряженных градиентов. Является попыткой объединить достоинства методов первого порядка (к ним относятся градиентные методы, так как на интервале шага они заменяют нелинейную функцию f(x) линейной) и второго порядка с исключением их недостатков;
- метод тяжелого шарика. Название метода происходит от аналогии с движением «тяжелого» материального шарика по наклонной поверхности.
Следующая группа численных методов оптимизации относится к методам многомерной безграничной оптимизации [20]. У этих методов величина и направление шага к оптимуму формируются однозначно, по определенным детерминированным функциям в зависимости от свойств, критерия оптимальности в окрестности текущей точки без использования производных. К методам названной группы относятся:
- метод Гаусса-Зайделя (метод покоординатного спуска). Метод прост в реализации. На эффективность метода влияет порядок чередования переменных. Недостаток метода состоит в низкой эффективности в овражных функциях, высокая чувствительность к выбору системы координат;
- метод Розенброка. Направлен на ликвидацию одного из недостатков предыдущего метода — высокую чувствительность к выбору системы;
- метод координат. Особенно эффективен для квадратичных функций;
- симплексный метод. (Симплексом в n-мерном пространстве называют фигуру, содержащую n + 1 вершину. На плоскости — это треугольник, в трехмерном пространстве — тетраэдр и т. д.);
- метод параллельных касательных. Данный метод эффективен, для задачи невысокой размерности для функций, близких к квадратичным функциям.
Ряд методов оптимизации можно объединить в группу методов многомерной случайной оптимизации [21]. Эффективны рассматриваемые методы и при поиске глобального оптимума. К методам названной группы можно отнести:
- метод слепого поиска;
- метод случайных направлений;
- метод поиска с «наказанием случайностью»;
- метод с «блуждающим» поиском.
Последняя группа методов — методы многомерной условной оптимизации [21]. К этой группе относятся численные методы построения улучшающих последовательностей при наличии ограничений типа равенств и типа неравенств. Сюда не входят методы, использующие условия оптимальности. Основными являются:
- метод штрафов;
- метод прямого поиска с возвратом;
- метод проектирования градиента.
Сущность приведенных выше методов оптимизации достаточно хорошо освещена в учебной и научной литературе по прикладной математике (в том числе, перечисленной в данной работе).
Заключение
Несмотря на то, что методы оптимизации как самостоятельное направление сложились еще в середине 1960-х гг., их развитие продолжается по сей день. Поэтому в одном исследовании невозможно рассмотреть все существующие классы задач и методы их решения.
На всех стадиях жизненного цикла предприятия, организации, фирмы приходится принимать множество решений. Любой предприниматель в ходе своей деятельности стоит перед проблемами выборами источников финансирования, задачи подбора помещения, найма работников, выбора стратегии предприятия, партнёров, источников сырья, проблемами сбыта продукции. Все решения этих сложных проблем приходится принимать в условиях недостатка информации и времени. Экономико-математические методы моделирования задач принятия решения помогут найти оптимальные решения. С помощью компьютерной техники, имея определённую модель, которая отражает основные свойства объекта и ситуации, можно рассмотреть различные варианты решений и определить оптимальное решение.
Оптимизационные задачи встречаются повсюду — в программировании, экономике, транспорте, в целом — практически во всех отраслях человеческой деятельности. Специалист должен уметь распознавать, когда стоящая перед ним задача относится к классу оптимизационных, и выбирать адекватные методы ее решения.
Список источников
- Абчук, В.А. Справочник по исследованию операций / В.А. Абчук. - М.: Воениздат, 1979. – 240 c.
- Лукин А.И. Системы массового обслуживания / А.И. Лукин. - М.: Воениздат, 1980. - 218 c.
- Понтрягин Л.С. Математическая теория оптимальных процессов /Л.С. Понтрягин. - М.: Наука, 1983. – 283 c..
- Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление /Л.Э. Эльсгольц. - М.: Наука, 1969. – 146 c.
- Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. / Б. Банди. – М.: Радио и связь, 1988. – 128 с.
- Хедли Дж. Нелинейное и динамическое программирование: Пер. с англ. /Дж. Хедли. – М.: Мир, 1969. – 424 с.
- Сухарев, А.Г. Курс методов оптимизации. / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров. – М.: Наука, 1986. – 328 с.
- Данциг Дж. Линейное программирование: Пер. с англ. / Дж. Данциг – М.: Прогресс. 1966. – 600 с. 9 Мину М. Математическое программирование. Теория и алгоритмы: Пер. с франц. / М. Мину. – М.: Наука, 1990. – 487 с.
- Фейгин М.И. Проявление эффектов бифуркационной памяти в поведении динамической системы // Соросовский образовательный журнал : журнал. — 2001. — Т. 7, № 3. — С. 121—127.
- Гурлев И.В. Цифровизация экономики России и проблемы роботизации // Вестник Евразийской науки, 2020 №4, https://esj.today/PDF/08ECVN420.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ.
- Фейгин М.И. Проявление эффектов бифуркационной памяти в поведении динамической системы // Соросовский образовательный журнал : журнал. — 2001. — Т. 7, № 3. — С. 121—127.
- Sorgner A. (2017) The Automation of Jobs: A Threat for Employment or a Source of New Entrepreneurial Opportunities? Foresight and STI Governance, vol. 11, no 3, pp. 37–48.
- Frey C.B., Osborne M.A. (2017) The future of employment: how susceptible are jobs to computerisation? Technological Forecasting and Social Change, vol. 114, pp. 254–280.
- Роботизация в России // Портал «РИТМ машиностроения» [Электронный ресурс] — Режим доступа: https://ritm-magazine.ru/ru/public/.
- Агентно-ориентированного подхода [Электронный ресурс] — Режим доступа: https://lektsia.com/1x885f.
- Minsky M. The Society of Mind. – NewYork: Simon and Shuster, 1986 [Электронный ресурс] – Режим доступа: http://www.acad.bg/ebook/ml/.
- Лукина Ю.Ю., Федяев О.И. Технология создания мультиагентных систем в инструментальной среде MadKit/ Информационные управляющие системы и компьютерный мониторинг-2011 / Материалы научно-технической конференции молодых учёных и студентов. — Донецк, ДонНТУ — 2011 [Электронный ресурс] — Режим доступа: http://ea.donntu.ru/handle/.
- Методология проектирования GAIA [Электронный ресурс] — Режим доступа: https://studopedia.ru/9_168381.
- MadKit Development Giude [Электронный ресурс] — Режим доступа: http://www.madkit.net/documentation/.
- Платформы для разработки МАС [Электронный ресурс] — Режим доступа: https://www.intuit.ru/studies/.