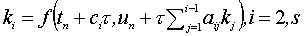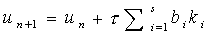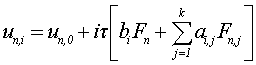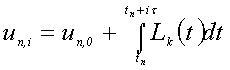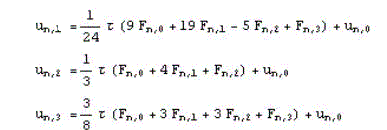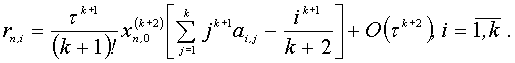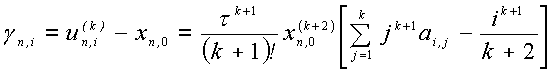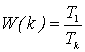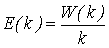Содержание
Введение
1. Анализ развития параллельных вычислений
2. Типовые топологии
3. Метод Рунге-Кутта решения задачи Коши для ОДУ
4. Параллельные одношаговые блочные методы решения задачи Коши для ОДУ
4.1. Формулы для трехточечного блочного метода
4.2. Погрешность аппроксимации
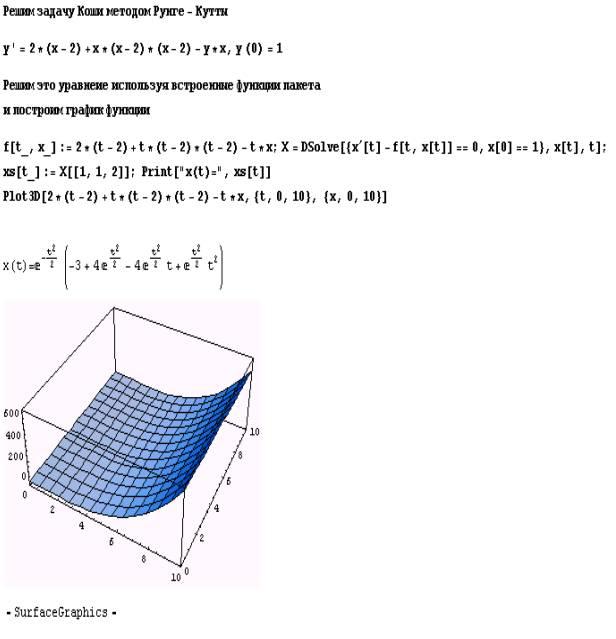
4.3. Пример решения задачи Коши для ОДУ блочным методом
4.4. Оценка эффективности
Выводы
Литература
Введение
С развитием техники перед учеными ставятся все более
сложные цели, достижение которых требует оригинального мышления и
повышенной внимательности. Постоянные исследования в области
разработки и создания высокопроизводительных вычислительных средств
позволяют решать фундаментальные и прикладные задачи.
Производительности современных ЭВМ недостаточно для обеспечения
нужного решения многих задач. Один из наиболее эффективных способов
повышения производительности заключается в распараллеливании
вычислений в многопроцессорных и параллельных структурах. Вследствие
чего, применение параллельных вычислительных систем является
довольно важным направлением развития вычислительной техники.
В последнее время появилось большое количество численных методов
интегрирования дифференциальных уравнений, которые ориентированы
на вычислительные системы с параллельной архитектурой. Однако практическое
использование большинства методов не всегда оправдано, поскольку многие из них
либо обладают численной неустойчивостью, либо имеют очень сложную структуру,
приводящую к потере эффективности. К методам, лишенным указанных недостатков,
можно отнести блочные. Блочным будем называть метод, при котором для блока из k
точек новые k значений функции вычисляются одновременно. Эта особенность методов,
во-первых, согласуется с архитектурой параллельных вычислительных систем, а,
во-вторых, позволяет вычислять коэффициенты разностных формул не в процессе интегрирования,
а на этапе разработки метода, что значительно увеличивает эффективность счета.
Однако, при всех их достоинствах эти методы рассмотрены довольно мало. Информация, в основном,
защищена и недоступна без регистрации или оплаты.
1 Анализ развития параллельных вычислений
Если в один и тот же момент времени выполняются одновременно
несколько операций обработки данных, то такие вычисления называются
параллельными[10]. Можно ускорить процесс решения задачи при помощи
разделения используемого алгоритма на некоторые независимые части,
которые будут выполняться на отдельных процессорах.[7]
Однако параллелизм до сих пор не получил широкого распространения.
Это обусловлено следующими факторами[3]:
-
Высокая стоимость параллельных вычислительных систем.
В соответствии с законом Гроша, производительность компьютера
возрастает пропорционально квадрату его стоимости и, следовательно,
более выгодно получить требуемую вычислительную мощность приобретением
одного производительного процессора, чем использование нескольких менее
быстродействующих процессоров. Но, следует учесть, что рост быстродействия
последовательных ЭВМ не может продолжаться бесконечно, кроме того,
даже наиболее мощные компьютеры подвержены быстрому моральному
старению. Тенденция же построения высокопроизводительных комплексов
из типовых элементов: микропроцессоров, микросхем памяти, коммуникационных
устройств, массовый выпуск которых освоен промышленностью, сильно снижает
влияние этого фактора[10].
-
Потери производительности для организации параллелизма – согласно
гипотезе Минского, ускорение, достигаемое при использовании параллельной
системы, пропорционально двоичному логарифму от числа процессоров,
то есть при 1000 процессорах возможное ускорение оказывается равным 10.
При этом существует большое количество задач, параллельное решение которых
достигается 100% использование всех имеющихся процессоров параллельной
вычислительной системы.
-
Постоянное совершенствование последовательных компьютеров –
в соответствии с законом Мура мощность последовательных процессоров
возрастает практически в два раза каждые 18–24 месяцев и, как результат,
необходимая производительность может быть достигнута и на обычных последовательных
компьютерах. Стоит отметить, что аналогичное развитие свойственно и параллельным системам.
-
Существование последовательных вычислений
– в соответствии с законом Амдаля [4] ускорение процесса вычислений
при использовании р процессоров ограничивается величиной
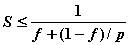 , , |
где f есть доля последовательных вычислений в применяемом алгоритме
обработке данных. Однако, часто доля последовательных действий характеризует
не возможность параллельного решения задач, а последовательные
свойства применяемых алгоритмов. И, следовательно, доля последовательных
вычислений может быть существенно снижена при выборе более подходящих
для распараллеливания алгоритмов.
-
Зависимость эффективности параллелизма от учета характерных
свойств параллельных систем – в отличие от единственности классификации
схемы фон Неймана последовательных ЭВМ параллельные системы отличаются
существенным разнообразием архитектурных принципов построения, и максимальный
эффект от использования параллелизма может быть получен только при полном
использовании всех особенностей аппаратуры. Следовательно, перенос параллельных
алгоритмов и программ между разными типами систем становится затруднительным.
С другой стороны, при всем разнообразии архитектур параллельных систем, тем не менее,
существуют и определенные способы обеспечения параллелизма.http://www.ispras.ru/
-
Существующее программное обеспечение ориентировано в основном
на последовательные ЭВМ. [9] Но, если последовательные программы
не позволяют получать решения новых задач за приемлемое время или же
возникает необходимость решения новых задач, то необходимой становится
разработка нового программного обеспечения, и эти программы могут быть
реализованы в параллельном варианте.
При выполнении параллельных вычислений в МВС для организации
взаимодействия, синхронизации и взаимоисключения параллельно выполняемых
процессов используется передача данных между процессорами вычислительной
среды. [8] Временные задержки при передаче данных по линиям связи могут
оказаться существенными (по сравнению с быстротой процессоров) и, как результат,
коммуникационная трудоемкость алгоритма оказывает существенное влияние на выбор
параллельных способов решения задач.
2 Типовые топологии
Структура линий связи (топология сети передачи данных) должна удовлетворять различным требованиям: [7]
-
должна обеспечиваться высокая связность;[2]
- должно обеспечиваться максимальное количество одновременных связей, чтобы средства
коммутации не ограничивали параллельную обработку информации. [3]
К числу типовых топологий обычно относят следующие схемы: линейка, кольцо,
решетка, тор, гиперкуб, клика, звезда.[2]
Линейка (linear
array or farm) – представляет собой линейный массив процессоров.(рис. 1)

Рисунок 1 – Сеть процессоров с топологией
линейка |
Решетка (2D-решетка,
матрица, сетка – mesh) – система, в которой граф линий связи
образует прямоугольную сетку, то есть процессоры расположены в виде
правильной двумерной решетки и каждый процессор (кроме крайних)
соединен с четырьмя соседями.[3]
Клика или полный граф
(completely-connected graph or clique) – система, в которой
между любой парой процессоров существует прямая линия.
Звезда (star) – система, в которой все процессоры имеют линии связи
с некоторыми управляющим процессором. (рис. 2)
Данная топология является эффективной при организации централизованных
схем параллельных вычислений.
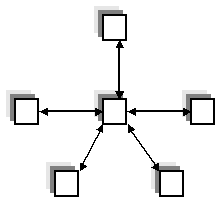
Рисунок 2 – Сеть с топологией звезда
|
Гиперкуб, или двоичный N-куб
Гиперкубическая архитектура впервые была разработана в Калифорнийском
технологическом институте; основной ее принцип состоит в использовании
множества микропроцессоров, каждый из которых снабжен локальной памятью,
для формирования вычислительных узлов, соединенных между собой
двухпунктовыми связями. Гиперкуб размерности n объединяет N=2n узлов,
которые независимо работают над выполнением отдельных частей полной
программы. Так, куб размерности 6 содержит 64 узла, каждый из которых
связан с шестью ближайшими соседями в пределах 6-размерного куба.Библиотека
Данные могут вводиться в узлы посредством сообщений, посылаемых по каналам
связи от процессоров, выполняемых в других узлах, или от управляющего
процессора куба. Для управления посылкой и получением сообщений служат
специальные примитивы операционной системы. Ширина полосы пропускания
сигналов связи гиперкуба растет с увеличением числа узлов пропорционально N
log2N, задержка в худшем случае составляет log2N.
Гиперкуб можно определить индуктивно; гиперкуб порядка N+1 может быть
построен путем удвоения гиперкуба порядка N и соединения двух наборов
узлов. Такой подход позволяет создавать программное обеспечение для
гиперкубов любых размерностей; необходимо лишь определить размерность на
время выполнения программы. Возможно также разделить большую
гуперкубическую машину на субкубы, отвести каждой программе узлы в
количестве, обеспечивающем максимально эффективное ее выполнение, и
использовать узлы, являющиеся в данный момент избыточными, для других
программ вместо того, чтобы оставлять их без применения.
Гиперкуб представляет собой сеть с максимально возможной плотностью
соединений; его объем может охватывать тысячи процессоров, потому что для
удвоения количества процессоров к каждому узлу должен быть добавлен всего
один коммуникационный канал. Плотность взаимосвязи узлов определяет
практичность использования всей системы соединений, представляющей собой
принципиально важную аппроксимацию параллельной вычислительной системы, так
как конкретная конфигурация связей зачастую непредсказуема.
Если узлы пронумерованы от 0 до 2n-1, каждый процессор непосредственно
связан со всеми теми, номера которых отличаются от его номера одной
двоичной цифрой. Отбрасывая некоторые связи гиперкуба, можно отобразить в
него многие другие виды сетевой топологии, к числу которых относятся
следующие:
-
решетки, или сетки размерностью до N;
-
кольца;
-
цилиндры;
-
тороиды;
-
топология ''бабочка'' для БПФ.
Реальные высокопроизводительные параллельные вычислительные
системы обычно используют несколько различных схем соединения
процессоров. Это позволяет сочетать лучшие качества известных топологий
и минимизировать недостатки.
Другим способом улучшить характеристики схем коммутации является
построение систем с изменяемой конфигурацией.
Изменять шаблон соединений можно как статически (до выполнения программы),
так и динамически (в ходе ее выполнения)[7].
Важнейшими атрибутами системы коммуникаций являются стратегии управления,
переключения и синхронизации. Что касается управления, то здесь можно
выделить две альтернативы: централизованное управление единым контроллером
(модулем управления) и распределенное управление. Примерами распределенного
управления являются работа многоступенчатых соединений, где каждый узел
принимает решение, как поступить с поступившим сообщением – оставить его
себе или передать соседу. Другой вариант используется, например, в соединениях
типа "звезда", где каждое сообщение пересылается в контроллер, который
определяет его дальнейшую судьбу.
Синхронизация тоже может быть глобальной, когда синхронизующая
последовательность импульсов передается всем узлам вычислительной системы,
но может быть и локальной, когда каждый узел имеет свой собственный генератор.
Последний вариант называется асинхронной работой. Преимущество глобальной
синхронизации, характерной для SIMD машин заключается в более простой
аппаратной и программной реализации, а асинхронные системы, чаще всего
это MIMD-компьютеры – более гибкие.Библиотека
Стратегии переключения тоже бывают двух видов. Во-первых, это пакетное
переключение, когда сообщение разбивается на более мелкие пакеты,
пересылаемые по сети. Преодолев очередное соединение, пакет попадает
на очередной узел, который определяет, куда этот пакет должен быть отправлен
и должен ли он быть отправлен вообще. В конце концов, пакеты должны прибыть
на узел-адресат, причем пути их могут быть разными. На последнем узле пакеты
собираются и восстанавливается переданное сообщение.
Во-вторых, возможно цепное переключение, когда между отправителем
и адресатом создается магистраль, по которой и передается сообщение целиком.
Решение различных прикладных задач требует решения обыкновенных
дифференциальных уравнений или систем обыкновенных дифференциальных
уравнений высокого порядка. Сокращение времени решения, а, следовательно,
и времени моделирования, возможно при использовании параллельных вычислительных
систем, эффективность работы которых существенно зависит от характеристик
применяемых параллельных алгоритмов.
3 Методы Рунге-Кутта решения задачи Коши для ОДУ.
Явный s-стадийный метод Рунге-Кутта состоит в следующем.
http://www.nsu.ru/
Пусть приближенное решение на n-ом шаге уже известно.
Задаются числовые коэффициенты формулы Рунге-Кутты
aij; ci i=2,s j=1,i-1; bi i=1,s
и последовательно вычисляются функции:
Затем по формуле
находится новое значение un+1.
Коэффициенты определяют вариант метода
Рунге-Кутта и выбираются из соображений точности.
Одним из возможных реализаций метода Рунге-Кутты четвертого
порядка точности может быть следующее: Библиотека
xn+1 = xn + h
yn+1 = yn + (1/6)(k1 + 2k2 + 2k3 + k4)
где
k1 = h f(xn, yn)
k2 = h f(xn + h/2, yn + k1/2)
k3 = h f(xn + h/2, yn + k2/2)
k4 = h f(xn + h, yn + k3)
Для любого варианта таких методов третьего порядка локальная
погрешность определяется первым неучтенным членом разложения
в ряд Тейлора, а глобальная погрешность определяется порядком
метода.
Рассмотрим решение задачи Коши для ОДУ методом Рунге-Кутты четвертого
порядка со следующими условиями:
y'=2*(x–2)+x*(x–2)2–y*x, y(0)=1:
4 Параллельные одношаговые
блочные методы решения задачи Коши для ОДУ. [1]
Рассмотрим решение задачи Коши для одного обыкновенного
дифференциального уравнения
x' = f(t,x), x(t0)=x0
одношаговым блочным методом.
Есть некоторое множество M точек равномерной сетки {tm}, m = 1,М и
tm=T с шагом t, которое разбивается на N блоков.
Каждый блок содержит k точек. N<=M.
Пусть i =0, k – номер каждой точки в каждом блоке n и
tn,i – точка с номером i, принадлежащая блоку n.
Точка tn,0 – начальная точка n-го блока.
Точка tn,k – конечная точка.
Отсюда видно, что имеет место равенство tn,k
=tn+1,0. При численном решении задачи Коши на
каждом шаге одновременно получаем новые k значений функции
и именно поэтому блочные методы достаточно хорошо реализуются
в параллельных ВС.
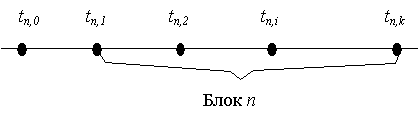
Рисунок 3 – Схема одношагового блочного
k-точечного метода.
|
Пусть un,0 –
приближенное значение решения задачи Коши в точке tn,0 –
начальной точке обрабатываемого блока.
Предположим, что в одном блоке все точки сетки находятся на равных расстояниях.
Тогда уравнения
одношаговых блочных разностных методов для блока из k точек может быть записано в виде:
Для определения
коэффициентов ai,j и bi нужно построить
интерполяционный многочлен Лагранжа Lk(t) с узлами
интерполяции tn,i , i= 0,1,…,k и соответствующими им
значениями Fn,i=f(tn,i, un,i)[6].
Далее требуется проинтегрировать его в пределах (tn,
tn + ih), i=1..k:
4.1 Формулы для
трехточечного блочного метода:
Построим интерполяционный
многочлен L3(t) с узлами интерполяции tn,i , i
= 0,1,2,3 и соответствующим им значениям правой части уравнения
Fn,i = f(tn,i, un,i) и далее
проинтегрируем его в соответствующих пределах.[1] Используя пакет
Mathematica, получим искомые формулы.
Формулы, которые были
получены для трехточечного блочного метода, определяют значение
приближенного решения неявно, а это значит, что возникает
необходимость решения системы уравнений относительно
un,1, un,2 и un,3.
Как можно видеть из рисунка 4: в отличие от обычного явного метода Рунге-Кутта, мы можем получить не одну точку за шаг,
а сразу k точек за один шаг:
Для запуска анимации нужно выбрать в контекстном меню (по правой клавише мыши) пункт Play.
4.2 Погрешность аппроксимации
Одношаговый k-точечный
блочный метод имеет наивысший порядок аппроксимации, равный k+1.[5]
А погрешность рассматриваемого метода имеет вид:
Главный член
локальной погрешности будет:
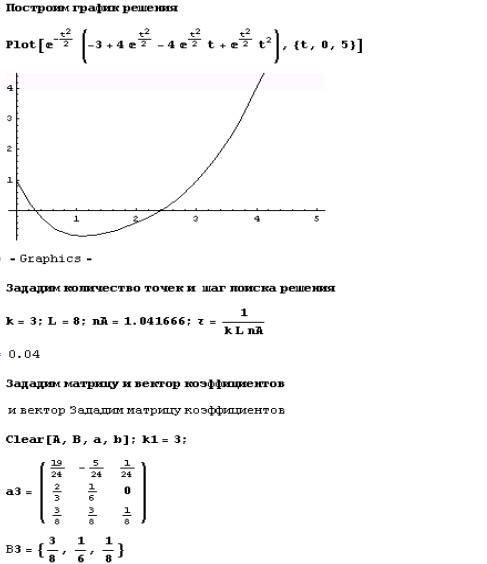
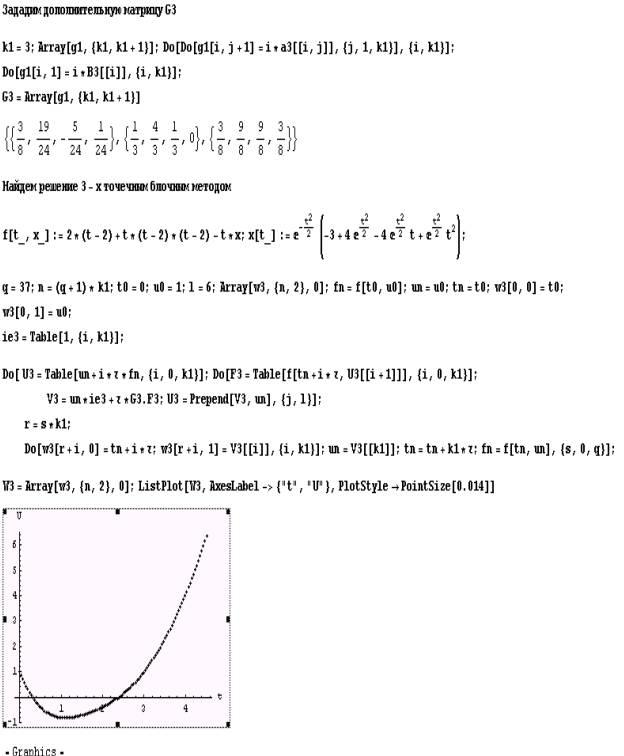
4.3 Пример решения задачи Коши для ОДУ блочным методом
При решении задач будем использовать пакет Mathematica.
4.4 Оценка
эффективности
В качестве одной из оценок степени
параллелизма алгоритма используется коэффициент ускорения[2]:
T1 – время
выполнения алгоритма Рунге-Кутта на однопроцессорной ЭВМ
Tk – время выполнения алгоритма Рунге-Кутта на
параллельной ВС
Если tf – время вычисления значения
функции f(t,x),
tad, tmul – время
выполнения операции сложения и умножения соответственно.
k –
количество узлов блока (равное количеству процессоров)
Время
вычисления на одном процессоре с точностью O(tk+1) во
всех k узлах блока по формулам Рунге-Кутта k+1 порядка точности: [1]
T1= k(k + 1)tf
+k2(tad +tmul)
Для определения
Tk возьмем ВС SIMD структуры с топологией кольцо. Каждый
процессорный элемент может выполнить любую арифметическую операцию
за один такт; временные затраты, связанные с обращением к
запоминающему устройству, отсутствуют.
Закрепим за каждым узлом
блока процессор. На k процессорах можно одновременно вычислять
значения F(s)n,i, а затем также одновременно
получить по формулам значения u(s)n,i для
каждого фиксированного s.
Если tta – время передачи
числа соседнему процессору, то время параллельного вычисления
приближенных значений решения с той же точностью для всех узлов
блока составит:
Tk =(k+1)tf
+k2(tad+ tmul)+k(k–1)tta
Если учитывать только время вычислений правой части уравнений,
т.к. времена выполнения арифметических операций и обмена значительно
меньше времени вычисления правой части, то ускорение k точечного
одношагового параллельного алгоритма можно считать приближенно
равным k.
В качестве еще одной оценки степени параллелизма
алгоритма используется коэффициент эффективности, который
определяется отношением ускорения к числу используемых процессорных
элементов, т. е.
Для рассматриваемого
случая: Е(k)=1.
Выводы
Практическое использование большинства методов численного
интегрирования дифференциальных уравнений, которые ориентированы
на вычислительные системы с параллельной архитектурой не всегда оправдано,
поскольку многие из них либо обладают численной неустойчивостью, либо имеют
очень сложную структуру, приводящую к потере эффективности. К методам,
лишенным указанных недостатков, можно отнести блочные.
k
точечный одношаговый блочный метод – метод, при котором для блока k
точек новые k значений функции вычисляются одновременно. Эта
особенность методов, во-первых, согласуется с архитектурой
параллельных вычислительных систем, а, во-вторых, позволяет
вычислять коэффициенты разностных формул не в процессе
интегрирования, а на этапе разработки метода, что значительно
увеличивает эффективность счета.
В дальнейшей работе я планирую перейти к решению систем обыкновенных
дифференциальных уравнений блочными методами. А также создать пакет,
расширяющий функциональные возможности пакета Mathematica при решении
и оценке эффективности задачи Коши для ОДУ.
Литература


 ,
,