ЭЛЕКТРОННАЯ БИБЛИОТЕКА

"Статьи по теме магистерской работы"

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК РОТОРНЫХ СИСТЕМ

Кулешов В.В., Архангельская Г.В. (Институт надёжности машин АНБ, г. Минск, РБ)

The calculation of dynamic characteristics of rotor systems by a matrix method of initial parameters is offered. The outcomes of simulation of rotor systems' simulation represented.

Задача расчёта и прогнозирования динамических характеристик роторных систем является актуальной при решении вопросов повышения надёжности их функционирования. Существующие методы определения динамических характеристик трудоёмкие и требуют высококвалифицированных специалистов. При расчёте сложных роторных систем, особенно с распределёнными массами и учётом изгибных деформаций наиболее приемлемым и доступным методом для расчёта динамических характеристик является матричный метод начальных параметров [1]. Данный метод наиболее универсален и позволяет рассчитывать динамические системы состоящие из ряда участков с различными параметрами.

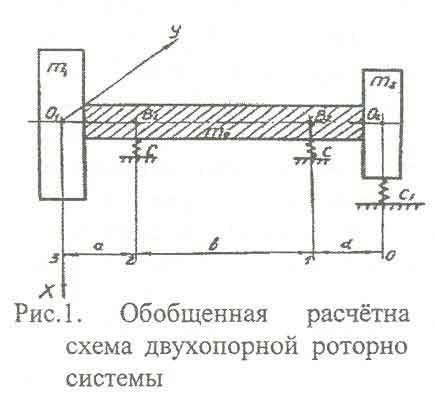
Для решения поставленной задачи большинство конструкций роторных систем можно рассматривать как двухконсольную балку, нагруженную сосредоточенными и распределёнными массами. Обобщённая схема таких роторных систем представлена на рис.1. Для данной схемы разработана математическая модель для расчёта собственных частот и форм колебаний ротора.

Расчёты форм колебаний ротора и критических частот системы ротор -опоры в значительной степени определяют выбор той или иной конструкции, размеры различных деталей и позволяют обеспечить надёжность работы на заданных режимах. В свою очередь взаимовлияние конструктивных параметров составляющих элементов роторной системы оказывают влияние на динамику ротора и должно учитываться при расчёте. Например, недостаточная жёсткость опор, нерациональное отношение длины консолей межопорному пролёту, а также необоснованный выбор диаметра ротор приводит к повышению уровня шума и вибраций системы в целом.

Собственные частоты w1, w2, ..., wn системы находятся путём решения уравнения:

Вычислим переходную матрицу системы, используя при этом каталог переходных матриц X [2].

Рассматриваемая роторная система состоит из двух масс т\ и т2 и гержня длиной /, разбиваемого на три участка с распределёнными масса-Ьи /яоь то и то2- В сечениях имеются линейно упругие опоры с жёстко-Ъъю С, а в сечении 0 ременная передача привода вращения ротора с жёсткостью С]. При расчёте собственных частот вязким демпфированием пренебрегаем.

Введём обозначения: EJ\, EJ2=EJ, EJ^ - изгибные жёсткости участ-к>в; у>1 - амплитуда перемещений в / - ом сечении; #>, - угол поворота; М-, -изгибающий момент; Q, - поперечная сила.

Матрицы столбцы параметров на концах ротора обозначим Yo и Yj. Выписываем из каталога [2] матрицы для первого участка ротора: Lo - мат-шца сосредоточенного груза в 0 - м сечении; QQ матрица жёсткости С] в I - м сечении; 77 - матрица зависимости между параметрами на концах рервого участка; Q - матрица перехода через опору.

Аналогичным образом продвигаясь от правого конца ротора к левому выписываем переходные матрицы для всех участков ротора. Результирующая матрица будет иметь вид:

Тогда уравнение, описывающее зависимость параметров на правом и ;евом концах ротора, можно записать в виде:

Из уравнений (4) получим уравнение частот (1)

В уравнение (5) входит w, решая его, находим конечное число собственных частот. Найдём форму колебаний шпинделя для собственной частоты со = ФК {к = 1,2,..., п). В этом случае определитель системы (4) равен нУлю, а каждое из уравнений системы является линейной комбинацией Другого и для определения двух неизвестных имеется, таким образом, одно уравнение (любое из (4)). Из первого уравнения определяем связь между параметрами.

Вычисляя функции Крылова Л(х,/,А,);В(х,1,Л,);С(х,1,Л);О(х,1,А) входящие в состав элементов переходных матриц участков, определяем матрицу /7роторной системы. Ввиду того, что переходные матрицы на каждом из участков ротора будут различны, форма колебаний на собственной частоте будет вычисляться по различным зависимостям для каждого участка.

Двигаясь от правого конца ротора к левому, получаем для l -го участка:

Из матричного уравнения (3) произвольно задав одно из амплитудных значений начальных параметров и осуществляя матричные преобразования начального вектора состояния, находим амплитудные прогибы у;{х) ротора в любом сечении при 0 < х < /,-, которые и будут определять форму колебаний ротора на собственной частоте для i'-го участка с точностью до константы Cj

Выбирая константы ci такими, чтобы функция"

была непрерывной, получим форму колебаний на всей длине шпинделя 0Для получения информации о влиянии конструктивных и рабочих параметров роторной системы на её динамические характеристики, проводились исследования разработанной модели на ПЭВМ на примере шпиндельного узла станка ЗЕ184.Исследования модели и выбор оптимальных параметров выполнялись по методике ЛП-лоиска [3]. Эта информация необходима как для анализа характеристик, так и для их оптимизации при заданных ограничениях, т.е. для синтеза структуры шпиндельного узла. По результатам исследований получены зависимости динамических характеристик шпиндельного узла от конструктивных и рабочих параметров.

Рисунок 2 - зависимость собственных частот ротора (номер частоты соответствует номеру кривой) от момента инерции J, массы инструмента - 1, 2, 3, 4 и жесткости С опор - Г,2\3\4\ при средних значениях остальных параметров.

Данные зависимости представлены на рис.2-3. Анализ полученных зависимостей показывает, что собственные частоты шпинделя зависят от жесткости опор. При жёсткости опор выше жёсткости шпинделя завися мость линейна, а при опорах с жёсткостью меньшей жёсткости шпинделя зависимость нелинейна. Момент инерции массы инструмента не оказывает влияния на значение первой и второй собственной частоты. Третья собственная частота с увеличением момента инерции массы инструмента изменяет своё значение по нелинейной зависимости, частот ротора (номер частоты описываемой монотонно убывающей соответствует номеру кривой) Функцией (рис.2). При изменении скорости вращения шпинделя форма динамического прогиба меняется. Для скоростей вращения' близких к критическим, динамический прогиб шпинделя увеличивается, а его форма приближается к форме свободных изгибных колебаний. Форма свободных колебаний шпинделя, имеющего консольный участок, обладает некоторыми особенностями.

На первой критической скорости шпинделя консольный участок почти не имеет собственного динамического прогиба и является жестким продолжением упругой линии шпинделя. На второй критической скорости появляется небольшой динамический прогиб собственно консоли, а на третьей сильно возрастает (рис.За-г).

Данные результаты использовались при отработке конструкции нового высокоскоростного шпиндельного узла с гидродинамическими опорами.

Список литературы: 1. Макеев В.П., Гриненко Н.И., Павлюк Ю.Г. Статистические задачи динамики упругих конструкций. - М: Наука, Главная редакция физико-математической литературы, 1984. - 232с. 2. Ивович В.А. Переходные матрицы в динамике упругих систем: Справочник. -2-е изд., доп. - М.: Машиностроение, 1981. - 183с, 3. Соболь И.М., Статников Р.Б, Выбор оптимальных параметров в задачах со многими критериями М.: Наука, 1981.- ПОс.