| Биография | Автореферат | Библиотека | Ссылки | Отчет | Индивидуальное задание |
The article deals with cold roiling of teeth with the help of rollers obtained in a space machine - tool engagement on onecavity hyperbolas.
В технологии финишной отделки зубьев цилиндрических колес часто применяют холодную обкатку зубьев взамен зубошевингования. В отличие от зубошевингования при обкатке окончательная обработка боковых поверхностей зубьев зубчатого колеса осуществляется без снятия стружки посредством пластического деформирования металла в холодном состоянии.
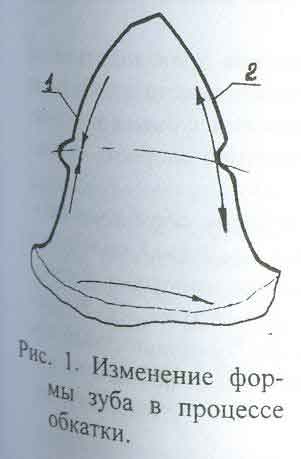
Во время процесса обкатки обрабатываемое зубчатое колесо и инструмент-обкатник, имеющий форму цилиндрического зубчатого колеса, находятся в беззазорном зацеплении. В результате взаимного относительного скольжения профилей зубьев заготовки и инструмента, на противоположных сторонах зуба материал припуска течет в разных направлениях []]. На ведомой стороне 1 профиля зуба колеса (рис.1.) металл перемещается от головки и ножки зуба к делительной окружности. В результате на делительной окружности происходит навалакивание металла - образуется выступ.
На противоположной стороне зуба 2 металл перемещается от де тельной окружности к головке и ножке зуба, в результате в зоне делит ной окружности появляется впадина. Кроме того, вследствие течения металла в сторону головки зуба, наружный диаметр обрабатываемого коп увеличивается. Различный характер деформаций и течения металла обеих сторонах зубьев создают трудности в получении симметрично профиля зуба обрабатываемого колеса. Чтобы получить удовлетворительные результаты, вводят различную коррекцию на каждой стороне зуба прикатника, что является сложной технологической задачей. При этом вели чину припуска под обкатку принимают небольшой, примерно в 2 щъ\ меньше, чем под шевингование, который находится в пределах 0,02 - О Oil мм. В настоящее время разработано несколько технологических схем для обкатки зубьев.
На станках, работающих при скрещивающихся осях, обеспечивается более равномерный перепад скоростей скольжения, но из-за точечного характера касания между обрабатываемым колесом и обкатником увеличивается интенсивность износа обкатника, в результате чего резко снижается его стойкость и в результате происходит потеря точности изделия [2] Кроме сказанного следует иметь в виду, что обкатник должен иметь подачу вдоль оси изделия.
Из приведенного выше следует: обкатка должна производиться ДО станках при скрещивающихся осях. При этом можно добиться:
1)линейного характера касания между обрабатываемыми зубьями и зуобьями обкатника,
2)выровнять по величине и направлению скорость скольжения по всему полю зацепления.
Чтобы получить линейный контакт между зубьями обрабатывз го цилиндрического колеса 1 и зубьями обкатника 2, последний полу пространственном станочном зацеплении при помощи накатника, катящегося копией обкатываемого цилиндрического колеса (рис -) ^ сматриваемом случае обкатник получим на теле вида "однополости параболоид". Линии контакта (рис. 3) получены в неподвижной сист ординат XYZ [3].
Определим скорость скольжения между зубьями обрабатываемо гиперболоидного обкатника 2. Пусть в станочном зацеплении с вращающимися осями колеса 1 и 2 вращаются вокруг осей Z1 и Z2,с угловыми скоростями w01 w02 (рис. 2)
Скорость точки обрабатываемого зуба цилиндрического колеса 1 в системе XYZ определяется уравнением:
где г ~ радиус-вектор точки обрабатываемого колеса.
Для определения скорости точки обкатника 2 в системе XYZ приведем вектор Щ2' к точке О, заменив его вектором щ и вектором -моментом
Здесь г02 = ОО2 - радиус-вектор, проведенный из точки приведения О к какой-нибудь точке линии действия вектора ш02; за такуюточку выбрана Ог.
Скорость точки гиперболоидного обкатника 2 определяется уравнением:
Вектор К<2) представляет геометрическую сумму двух скоростей: вращательного движения вокруг оси О с угловой скоростью й>12) и поступательного движения со скоростью, определяемого вектором-моментом то(й)(2)).
Скорость движения точки, жестко связанной с цилиндрическим колесом, относительно той же точки, жестко связанной с гиперболоидным Иком 2> определится уравнением:
Относительное движение колеса 1 по отношению к обкатнику 2 определяется вектором w0(12) = W01-W02 проходящим через точку приведения О и вектором-моментом- m0w(2).
Найдем проекцию V приняв во внимание что:
где i,j,k - орты координатных осей.
Не нарушая общности, примем, что
В результате получим:
Для того чтобы получить истинные значения проекций скорости носительного движения, правые части выражений (8) необходимо умножить на величину й>(|> угловой скорости вращения зубчатого колеса 1.
В уравнениях (8) х, у, z - координаты точек зубьев колеса 1 в непод! вижной системе координат, и - передаточное число, у - углы скрещивания осей, aw - кратчайшее межосевое расстояние.
Проведем исследование скорости скольжения при обкатке гипербо-лоидными обкатниками зубьев цилиндрического прямозубого колеса со следующими геометрическими параметрами: модуль т=1 мм, количество зубьев Z]=76, делительный диаметр d\=mZ^lb мм, диаметр впадин df^dr -2,5m=73,5 мм, наружный диаметр da=dj +2m=78 мм.
Геометрические размеры гиперболоидного обкатника (в статье рассматривается два обкатника): количество зубьев Z2=7 и 16; модуль нормальный т=\ мм, угол скрещивания осей /^90 ...180° (рис. 2). При у - 380 оси обкатника и обкатываемого прямозубого колеса параллельны и обкатник становится прямозубым цилиндрическим колесом. Угол наклона зубьев на гиперболоидном обкатнике определяется со следуюШег0 уравнения /7 = 180 -у. Из изложенного следует, что геометрия гиперболоидного обкатника изменяется в зависимости от угла наклона [3, т.е. в з висимости от принятого угла скрещивания осей у. Для примера рассчитаем гиперболоидные обкатники с Z-f=l и Zj=\b, m=\ мм. Геометрические размеры гиперболоидных обкатников изменяются в зависимости от Уг скрещивания осей у (угла /3 наклона зуба в горловом сечении). Определим делительные диаметры искомых гиперболоидных обкатников в гор вых сечениях (min диаметр накатника) по известной из ТММ зависимости:
Из приведенных расчетов следует, что при малых углах наклона 0 диаметры гиперболоидных обкатников принимают небольшие значения. Чтобы увеличить диаметры обкатников, необходимо количество зубьев Z2 увеличивать.
Для нахождения наружных диаметров гиперболоидных обкатников в горловом сечении необходимо к делительному диаметру d2 прибавить 2,5т (две высоты головки), а диаметры впадин будут определяться из известной зависимости df2=d2-2m (две ножки).
Выразив в выражениях (8) координаты х, у я z обкатываемого цилиндрического эвольвентного колеса с параметрами Z,=76, m=1 мм в неподвижной системе координат S(XYZ), вычислим относительную скорость (скорость скольжения).
На рис. 4 приведены скорости скольжения, направленные по профилю эвольвентного зуба. Анализ численных значений показывает, что профильное скольжение зависит от угла скрещивания у осей гиперболой одного обкатника и цилиндрического зубчатого колеса.
При этом в интервале углов у = 90°...135° профильное скольжение !ie меняет знак. Это показывает, что профильная подача направлена в одну сторону по всему профилю, и при обкатывании колес не будет возникать в области длительной окружности "впадин" и "выступов". Самые благоприятные условия обкатки по этому показателю (профильное скольжение) находятся в интервале углов ;/= 90° - 130°. Поэтому при конструировании гиперболоидных обкатников их размеры рассчитаться при г = 90°-130°.
Таким образом, при обкатывании зубьев гиперболоидными обкатниками можно найти такие углы скрещивания осей у, при которых профильное скольжение направлено в одну сторону по всему профилю и по ве чине практически не изменяется. Заметим, что относительное скольжен VK '' практически равно скольжению Vz вдоль оси обрабатываемой, цилиндрического колеса, что благоприятно влияет па процесс обкатки зубьев цилиндрических колес.
Список литературы: 1. Производство зубчатых колес /Справочник под ред. Тайца Б.А. - М.: Машиностроение, 1975. - 728с. 2. Сухорукое Ю.Н., Евстигнеев Р.И. Инструменты для обработки зубчатых колес методом свободного обката. - К.:"Техника", 1983. - 121с. 3. Вітренко В.О. Гіпербобоідні інструменти для обробки i обладнання циліндричних прямозубих зубчатих коліс: Автореф. дис. д-ра техн. наук:О5.ОЗ.О1 / Націнальний політехнічний університет України. - К., 1995. - 32с
| Биография | Автореферат | Библиотека | Ссылки | Отчет | Индивидуальное задание |