Автореферат

Gogolenko Sergiy

Тема магистерской работы:

"Исcледование локально—детерминистических методов математического программирования"

Автор: С.Ю. Гоголенко
Научный руководитель: проф. д.т.н. В.А. Святный
Консультанты: М. Гинкель, К. Теплинский

e-mails:    gogolenkos@ukr.net
sergiy.gogolenko@gmail.com

Содержание

  1. Введение
    1. Задачи оптимизации, возникающие при моделировании СДС
      1. Особенности оптимизационных задач, возникающих при моделировании СДС
      2. Задача оценки параметров модели. Метод множественных стрельб
    2. Алгоритмы оптимизации
      1. Классификация алгоритмов оптимизации
      2. Обзор существующего оптимизационного ПО
    3. Обзор публиуаций по теме
    4. Краткое описание используемых алгоритмов
  2. Выводы
  3. Список использованной литературы

Введение


Поиск эффективных решений задачи оптимизации всегда был одним из наиболее приоритетных направлений прикладной математики. Высокая заинтересованность результатами данной области прикладной математики обусловлена как наличием в природе естественных оптимизационных процессов, так и стремлением человека к наилучшей организации своей деятельности. Таким образом оптимизация является важным инструментом при исследование рзличных физических систем и при принятии решений.

Целью данной работы является исследование подходов, базирующихся на использование локально-детерминистических методов, к решению различных оптимизационных задач, которые возникают при моделировании сложных динамических систем, а также построение эффективных локально-детерминистических алгоритмов оптимизации для решения этих задач. Для достижения поставленных целей в данной работе анализируется специфика, характерные черты и различные способы постановки наиболее важных в моделировании сложных динамических систем оптимизационных задач, а также изучаются известные алгоритмы для решения оптимизационных задач и реализующие их программные пакеты. Практическим результатом работы является разработка подсистемы оптимизации и внедрение её в моделирующую среду Diana, на базе которой и проводятся дальнейшие исследования.

Предполагается, что в рамках данной работы будет разработан новый эффективный алгоритм оптимизации (или группа алгоритмов), ориентированный на решение специфических задач, возникающих при моделировании сложных динамических систем.

Вверх

1. Задачи оптимизации, возникающие при моделировании СДС


1.1 Особенности оптимизационных задач, возникающих при моделировании СДС


Детальное рассмотрение всевозможных оптимизационных задач, возникающиих при моделировании СДС, позволяет разбить их на две группы.

К первой группе относятся задачи, в которых целевая функция и функции ограничения задаются формулами в явном виде. Подобные задачи обычно возникают в качестве подзадач других более крупных задач моделирования. Они характеризуются незначительной ценой вычисления целевой функции, а также малым либо средним числом неизвестных. Градиент для таких задач вычисляется зачастую с использованием конечноразностных схем отдельно от целевой функции. Наиболее часто область допустимых значений для задач первой группы полностью определяется функциональными ограничениями. Решение таких задач, в основном, не требует больших временных затрат и может быть найдено с использованием классических оптимизационных схем.

Ко второй группе относятся задачи, в которых целевая функция задаётся в виде суперпозиции некоторой функции и функции-решения системы дифференциальных уравнений (ДУ), описываюшей модель. Если модель описывается системой ДУ вида:

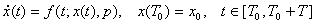\dot{x}=f(t;x,p); x(T_0)=x_0   (1.1)

то формально целевая функция для задач второй группы в общем виде описывается уравнением:
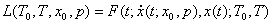L(t;x,p)=F(t;\dot{x},x,p)   (1.2)

Таким задачам присущи следующие особенности:
  1. Число неизвестных в данных задачах не велико и редко превышает 30.
  2. В связи с необходимостью интегрирования траектории при расчёте значения целевой функции, ее вычисление требует больших вычислительных затрат.
  3. Поскольку большинство специализированных интеграторов выполняют интегрирование траектории и анализ чувствительностей одновременно, то расчёт целевой функции и её градиента (либо якобиана её составляющих) могут быть выполнены также одновременно с минимальными дополнительными вычислительными издержками.
  4. Возможные случаи несходимости алгоритмов решения ДУ и невычислимости некоторых выражений, входящих в состав модельных уравнений, обуславливают появление прямых ограничений, которые на практике сложно (или невозможно) заменить эквивалентными функциональными ограничениями.
  5. Целевая функция в таких задачах зачастую характеризуется высокой нелинейностью и имеет множество локальных минимумов, что требует применения особых методов до начала использования локально-детермического алгоритма, обеспечивающих хорошее начальное приближение, а следовательно и глобализацию сходимости.
  6. Часто данные задачи плохо масштабируемы.

Из перечисленных особенностей следует, что задачи, принадлежащие ко второй группе, требуют значительной переработки классических алгоритмов оптимизации, ориентируя данные алгоритмы на как можно меньшее число вычислений целевой функции и учёт возникающих прямых ограничений.

Вверх

1.2 Задача оценки параметров модели. Метод множественных стрельб


Ко второй группе задач относится, в частности, задача оценки параметров модели. Постановка данной задачи может быть произведена следующим образом [6, 8, 13, 14]. Дана модель, описываемая системой ДУ (1.1) и набор уравнений наблюдения 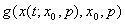g(x(t;x_0,p),x_0,p). Часть параметров p' и начальных значений переменных состояния x0' системы, описывающей модель, не известны и образуют вектор искомых параметров 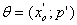\teta=(x_0^{'},p^{'}). В то же время известна матрица замеров Y, описывающая экспериментальные данные. Элементы матрицы Y являются замерами переменных состояния, с учётом функций наблюдения, в дискретные моменты времени и описываются уравнением:

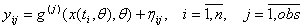y_{ij}=g^{(j)}(x(t;x_0,p),x_0,p),   (1.3)

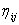где \eta - некоторый случайный шум, распределённый в большинстве случаев по нормальному закону. Целью является оценка вектора искомых параметров, исходя из экспериментальных данных. Обычно для решения этой задачи используют принцип максимального правдоподобия. Тогда в случае распределения шума наблюдения по закону Гаусса задача принимает вид:
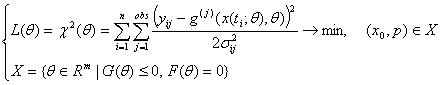L(x_0,p) = \sum_{i=1}^n \sum_{j=1}^{obs} \frac{ (x^{(j)}(t_i;x_0,p)-x_i^{(j)})^2}{2\sigma_{ij}^2},   (1.4)

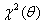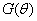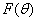где \hi^2(\teta) — целевая функция, а G(\teta) и F(\teta) — ограничения, накладываемые на целевую функцию, исходя из физических соображений. Доверительные интервалы для оцениваемых величин определяются посредством использования информационно матрицы Фишера [6, 12, 14] или других схожих методов [8].

Важной проблемой при использовании локально-детерминистических методов в данном случае является выбор начальной точки. Существует два подхода к решению этой проблемы. Первый из них называется подходом с оценкой начальной точки (initial-value approach) [8]. Он заключается в том, что после подходящего выбора начального приближения модельные уравнения интегрируются на всём временном промежутке оценки параметров, а затем вычисляется функция 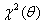\hi^2(\teta) по формуле (1.4). Данный подход требует использования на начальном этапе метода, обеспечивающего грубое приближение к глобальному минимуму. Наиболее простым выходом из этой ситуации является использование некоторого глобального стохастического оптимизатора. В данной работе в качестве такового выбран генетический алгоритм оптимизации.

Существует и альтернативный подход, именуемый методом множественных стрельб (ММС) [6, 8, 13, 14], впервые предложенный ван Домселааром и Хемкером (1975) и теоретически обоснованный Боком (1981,1983). Данный подход заключается в следующем. Сначала временной промежуток оценки параметров разбивается подходящим образом сеткой на подинтервалы T0=t0<t1<...<tm=T0+T (рис.1). Каждому из подинтервалов ставится в соответствие свой кусок интегрируемой траектории с собственными неизвестными начальными значениями переменных состояния x0(k). Искомые параметры модели p' при этом для всех интервалов остаются общими. В каждый интервал должна попадать по крайней мере одна экспериментальная точка. Поскольку результирующая траектория не должна иметь разрывов, к результирующим ограничениям добавляется ряд ограничений, обеспечивающих непрерывность результирующей траектории в момент переходов между интервалами. Окончательно задача принимает следующий вид:

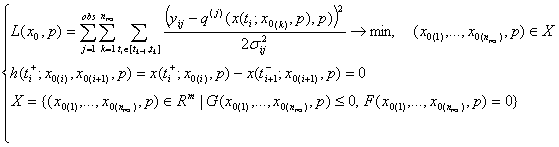L(x_0,p) = \sum_{i=1}^n \sum_{j=1}^{obs} \frac{ (x^{(j)}(t_i;x_0,p)-x_i^{(j)})^2}{2\sigma_{ij}^2}.   (1.5)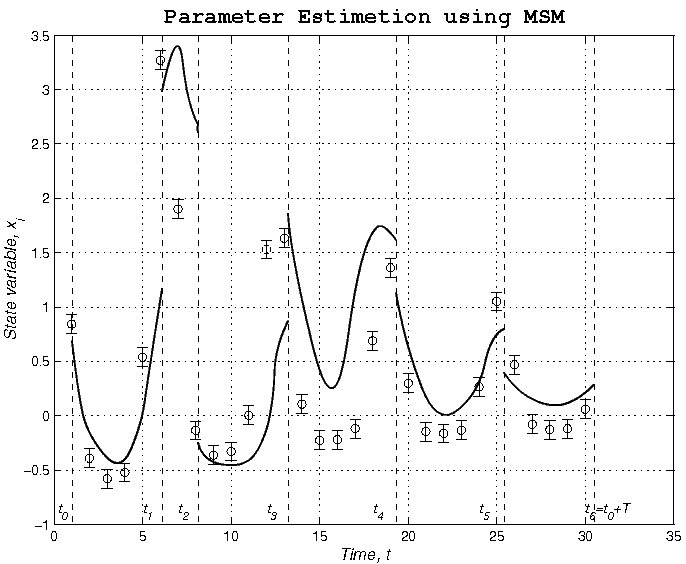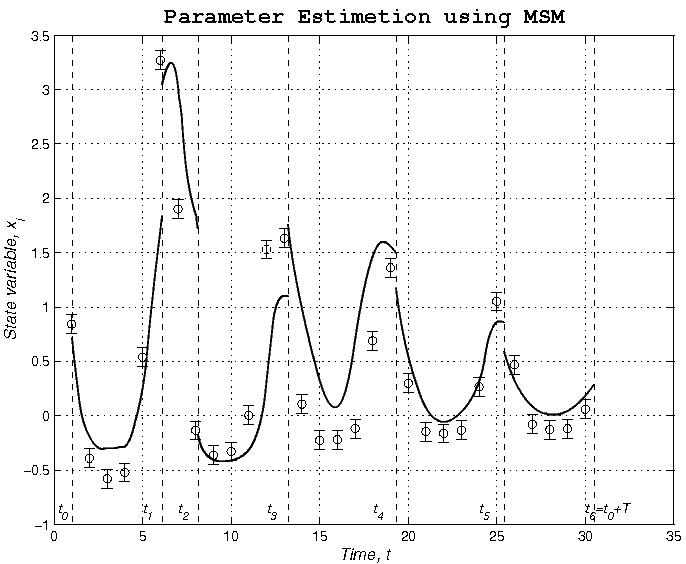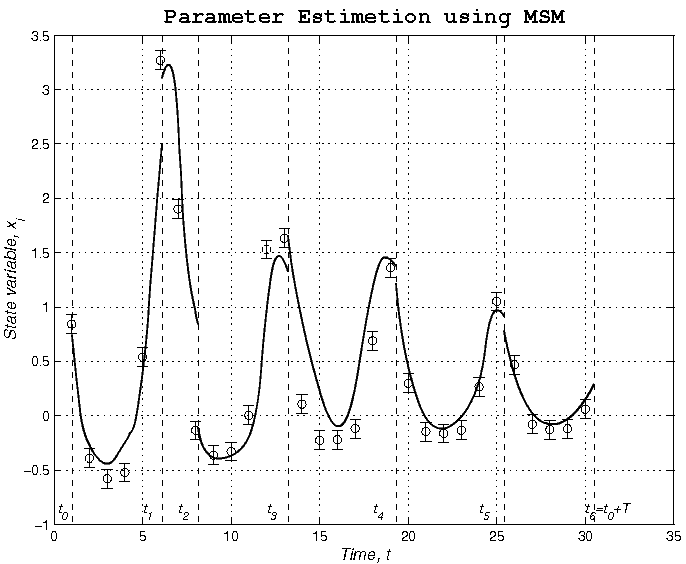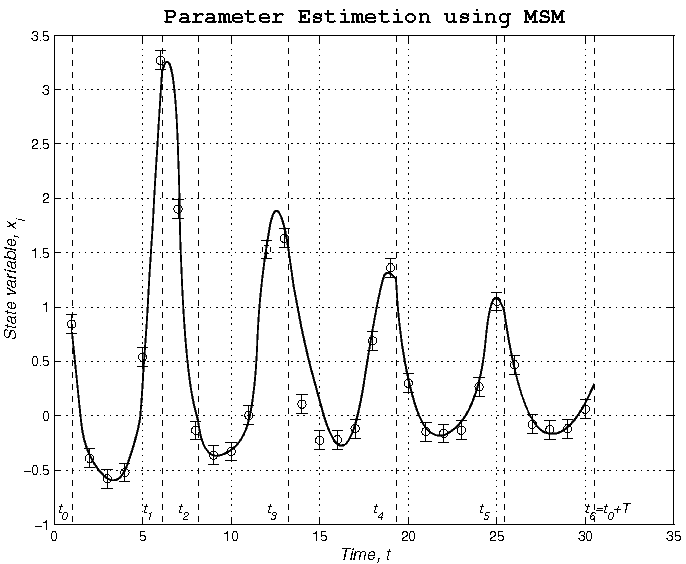

MSM idea
Рис.1.1 — Идея метода множественных стрельб

Несмотря на значительный рост числа неизвестных в ММС, данная схема обладает рядом преимуществ [13]:

  1. Упрощается учёт априорной информации о переменных состояния, определяемой по значениям замеров, при выборе начального приближения.
  2. Подходящий выбор начальной точки обычно позволяет избежать выхода на локальный минимум задачи.
  3. Данный метод является численно устойчивым и позволяет решать задачу оценки параметров даже для нестабильных и хоатических систем.
  4. Особая структура целевой функции позволяет упростить реализацию параллельных алгоритмов её подсчёта.

Вверх

2. Алгоритмы оптимизации


2.1 Классификация алгоритмов оптимизации


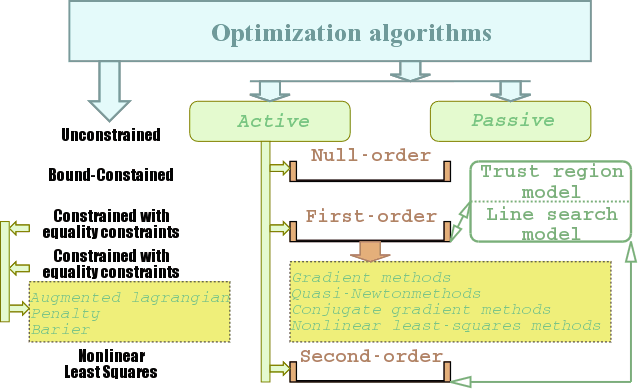
Существует несколько альтернативных подходов к классификации локально-детерминистических алгоритмов оптимизации (рис.2.1).

Критерием разделения алгоритмов на группы в первом подходе является класс оптимизационных задач, которые позволяет решить алгоритм [1, 2, 3, 5]. Поскольку наиболее важными частными случаями задачи математического программирования являются задача безусловной оптимизации, задача оптимизации с прямыми ограничениями на переменные, задача условной оптимизации с ограничениями-равенствами, задача условной оптимизации со смешанными ограничениями и задача минимизации функций нелинейных квадратов, то согласно этому критерию выделяют следующие группы алгоритмов:

  1. алгоритмы безусловной оптимизации;
  2. алгоритмы решения задачи оптимизации с прямыми ограничениями на переменные;
  3. алгоритмы условной оптимизации для задач с ограничениями-равенствами;
  4. алгоритмы условной оптимизации для задач со смешанными ограничениями;
  5. алгоритмы нелинейных наименьших квадратов.

Второй подход основывается на учёте различных критериев, которые определяют характерные черты реализации алгоритмов [4, 11]. Согласно одному из таких критериев методы оптимизации делятся на активные (последовательные) и пассивные. В пассивных методах все точки для дальнейшего анализа выбираются одновременно до начала вычислений. В активных методах точки выбираются последовательно, выбор каждой последующей точки зависит от значений предыдущих. Другим критерием классификации является информация о функции, которую требует алгоритм. Если для успешного выполнения алгоритма достаточно лишь информации о значение функции в точке, то такой алгоритм относится к алгоритмам нулевого порядка (метод Гаусса, симплексный метод Недлера-Мида, методы поворота системи координат Хука-Дживса, классический Розенброка, метод Пауэлла и т.д.). Если дополнительно требуется знание о градиенте, то алгоритм относится к алгоритмам первого порядка. Алгоритмы второго порядка кроме знания значение функции в точке и её градиента, нуждаются также в информации о матрице Гессе (метод Ньютона, классические SQP-схемы). Среди локально-детерминистических методов оптимизации наиболее представительную группу составляют методы спуска, которые в свою очередь базируются на двух моделях. Первую модель образуют методы линейного поиска, в которых на каждой итерации направление спуска определяется однозначно, а оцениванию подлежит длина шага. Вторую модель образуют методы доверительных областей (trust-region), в которых наоборот на каждой итерации оценивается направление спуска. Среди методов спуска первого порядка можно выделить такие группы методов [1, 9]:

  1. градиентные алгоритмы;
  2. квазиньютоновские алгоритмы (ДФП, БФГШ, SR1);
  3. методы сопрпяжённых направлений (метод Флетчера-Ривза, метод Полака-Рибьера);
  4. специализированные алгоритмы минимизации квадратов нелинейных функций (метод Гаусса-Ньютона, метод Левенберга-Маркарда, ряд SQP-схем).

optimization algorithms
Рис.2.1 — Классификация алгоритмов, решающих задачу математического программирования
Вверх

2.2 Обзор существующего оптимизационного ПО


На сегодняшний день разработано множество оптимизационных программ, реализующих локально детерминистические алгоритмы. Многие из этих кодов распространяется под лицензией GPL, часть напротив является платной либо частично платной. Условно всё оптимизационное ПО можно разбить на три группы (рис.2.2)[5]:

  1. программные пакеты, ориентированные на решение задачи математического программирования (на рис. оттенки зелёного);
  2. численные библиотеки, содержащие алгоритмы оптимизации (на рис. жёлтый цвет);
  3. системы оптимизации и моделирующие среды (на рис. синий цвет).

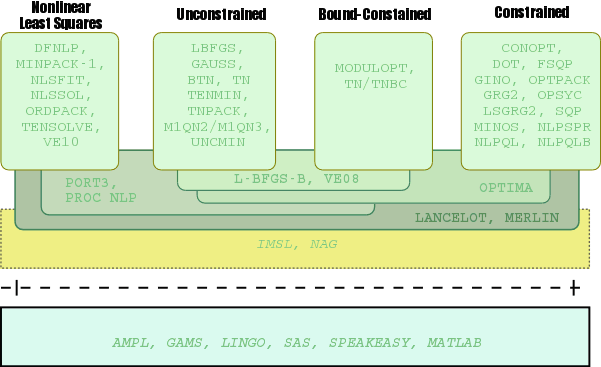
optimization software
Рис.2.2 — Классификация ПО, решающего задачу математического программирования

Часть из известных оптимизационных пакетов ориентирована на решение только одного класса оптимизационных задач, но некоторые пакеты способны эффективно решать несколько классов задач. Характерной чертой пакетов для решения задачи оптимизации с прямыми ограничениями на переменные является то, что они достаточно эффективно справляются с задачей безусловной оптимизации. Большинство оптимизационных пакетов реализованы на языке Fortran. Наиболее известными из них являются LANCELOT и MERLIN. Именно с эффективностью реализованных в них процедур обычно производится сравнение эффективности новых алгоритмов. LANCELOT является одной из наиболее мощных библиотек оптимизационных алгоритмов, ориентированных прежде всего на решение задач большой размерности. Язык реализации библиотеки — ANSI Fortran 77. Хотя недавно вышла адаптация пакета LANCELOT на Fortran 99. На данный момент LANCELOT разработкой занимается Council for the Central Laboratory of the Research Councils (CCLRC). Пакет MERLIN был разработан в университете г.Иоаннина (Греция) и первоначально предназначался для решения задачи оптимизации с прямыми ограничениями на переменные. Сейчас функциональность пакета значительно расширилась. Одним из наиболее известных пакетов для решения задач безусловной оптимизации и оптимизации с прямыми ограничениями на переменные на сегодня является пакет L-BFGS-B, разработанный в Северо-Западном университете (США). С недавнего времени начали появляться оптимизационные пакеты, реализованные на C++ (OptSolve++, OPT++, macopt). Часто такие пакеты уже содержат реализации параллельных алгоритмов оптимизации (OptSolve++, Bob++).

Численные библиотеки NAG, HSL и IMSL среди прочих неспециализированных численных библиотек выделяются наиболее развитой системой алгоритмов оптимизации. В библиотеке NAG алгоритмы оптимизации собраны в папку E04. Разработкой библиотеки занимается The Numerical Algorithms Group Ltd. На данный момент доступны реализации библиотеки на Fortran и C, в недавнем прошлом сушествовали только Fortran77 и Algol68 версии библиотеки. Библиотека является коммерческой. Библиотека HSL (Harwell Subroutine Library) разрабатывается CCLRC (в деревушке Харвел неподалёку от Оксфордшира). На данный моент библиотека HSL реализована только на ISO Fortran. Последний известный релиз библиотеки состоялся в сентябре 2004. Алгоритмы оптимизации библиотеки IMSL собраны в главу 8 её реализации на языке ANSI Fortran. Реализация библиотеки на C содержит только часть этих алгоритмов. Доступны также ограниченные реализации этой библиотеке на Java и C#.NET. Разработкой библиотеки занимается компания Visual Numerics Inc.

Системы оптимизации и моделирующие среды обычно представляют из себя развитый законченый продукт и имеют встроенный собственный (либо стандартизированный) язык моделирования, позволяющий достаточно просто формулировать оптимизационные задачи. Обычно такие системы и среды предоставляют интерфейс для подключения внешних пакетов, реализованных на Fortrn и C. Более того, моделирующая среда GAMS, разработанная GAMS Development Corporation, не имеет собственных оптимизационных кодов, а лишь предоставляет интерфейс для подключения пакета MINOS. Системы оптимизации Speakeasy также имеет интерфейс для подключения внешней библиотеки NAG, но в то же время в ней содержатся и "родные" пакеты, такие как EISPACK и FFTPACK. AMPL представляет из себя специализированный достаточно гибкий язык моделирования для постановки и решения задач математического программирования. Matlab является наиболее известной системой из вышеперечисленных. В данной системе реализованы квазиньютоновские алгоритмы, метод Недлера-Мида, метод Ньютона, метод Левенберга-Маркарда и т.д.

Существуют также пакеты, ориентированные на решение задачи оценки параметров. К ним следует отнести пакеты EASY-FIT, разработанный в университете г.Бейрут под руководством проф. К.Шитковского, и пакет PAREST, разработанный в Мюнхенском техническом университете. Причём в пакете PAREST реализован метод множественных стрельб.

К оптимизационному ПО стоит также отнести библиотеку тестовых оптимизационных задач CUTEr, разработанную Н.Гоулдом, Д.Орбаном и Ф.Тоинтом. Данная библиотека, по сути, является стандартом для тестирования алгоритмов оптимизации.

Вверх

3. Обзор публиуаций по теме


Ежегодно появляются десяки публикаций, посвящённых оптимизационным задачам, возникающих при моделировании СДС, и в частности вопросам оценки параметров моделеи. Не смотря на то, что сушествует множество основательных трудов в области оценки параметров [19, 20], метод множественных стрельб достаточно слабо освещён в литературе. Классические книги проф. Х.Бока, в которых проведено обоснование и доказательство практической ценности ММС, из-за малого тиража практически недоступны. Статей посвящённых ММС также относительно не много. В большинстве из них производится только обзор метода, а также способов его реализации. Анализ сходимости и другие важные вещи там отсутствуют.

Существует множество книг и статей, посвящённых локально-детерминистическим методам оптимизации. В части из них авторы пытаются охватить весь круг известных на данный момент локально-детерминистическим алгоритмов оптимизации, в некоторых работах авторы освещают лишь отдельный выбранный алгоритм либо группу методов.

Поскольку в данной работе в первую очередь планируется реализовать модификацию БФГШ-метода для решения задачи оптимизации с прямыми ограничениями на переменные, то в дальнейшем здесь будут рассматриваться только публикации, в которых описывается БФГШ-метод. Метод Бройдена-Флетчера-Голдфарба-Шэнно (БФГШ) был предложен в 1970 году [15-18] как развитие общей идеи квазиньютоновских методов, предложенной Давидоном. На сегодняшний день этот метод является наиболее эффективным квазиньютоновским методом. В 1980 Дж.Ноцедалем была предложена модификация БФГШ-алгоритма, требующая небольших затрат оперативной памяти и известная под названием LBFGS-метода [1, 7, 21], а в 1991 году им же в соавторстве с Р.Бёрдом был предложен L-BFGS-B-метод, позволяющий решать не только задачи безусловной оптимизации, но и задачи оптимизации с прямыми ограничениями на переменные [7]. В 1994 году появился пакет, реализующий LBFGS-B-алгоритм на языке Fortran. В 1994 году вышел последний релиз этого пакета. В дальнейшем публикации, касающиеся LBFGS появлялись ежегодно, но принципиально новых идей по модификацие LBFGS-алгоритма в них не было.

Вверх

4. Краткое описание используемых алгоритмов


В данной работе для решения оптимизационных задач, возникающих при моделировании СДС, используется подход с оценкой начальной точки (см. пункт 1.2). При этом начальное приближение к глобальному минимуму отыскивается с помощью генетического алгоритма оптимизации. В случае задачи оценки параметров дополнительно применяется метод множественных стрельб (см. пункт 1.2).

В качестве основного алгоритма оптимизации на данном этапе используется LBFGS-B-метод [7]. Направление в данном методе ищется согласно формуле (4.1):

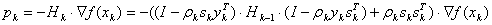p_k=-H_k \nabla f(x_k),   (4.1)

где s_k, y_k, \ro _k.

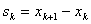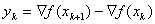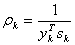Для учёта ограничений в LBFGS-B-алгоритме используется схема, идентичная той, которая применяется в методе проекции градиента. Классический LBFGS-B-алгоритм использует при выборе длины шага процедуру "бэктрэкинга" ("backtracking"). В данной работе планируется несколько улучшить классическую схему LBFGS-B-метода путём использования в нём при выборе длины шага интерполяционной процедуры.

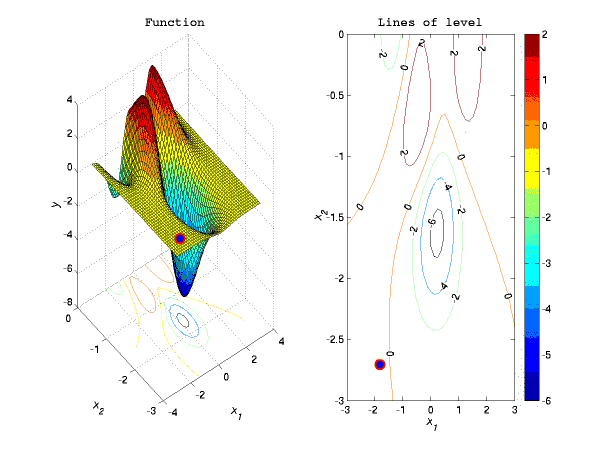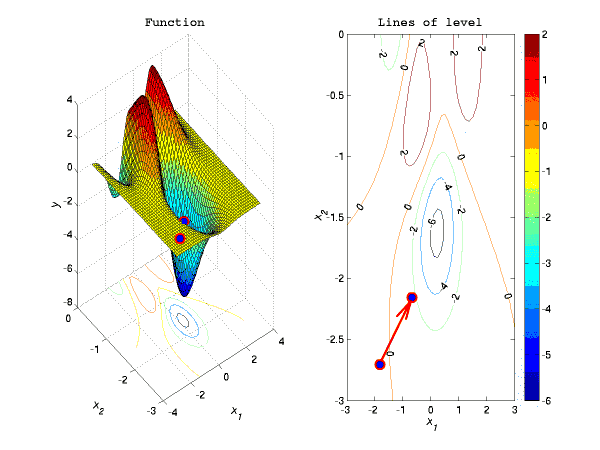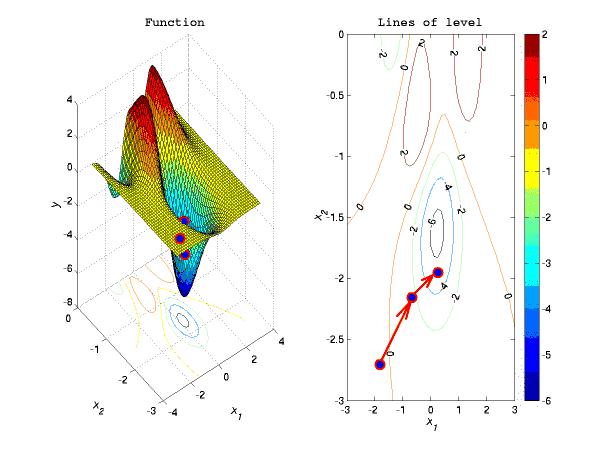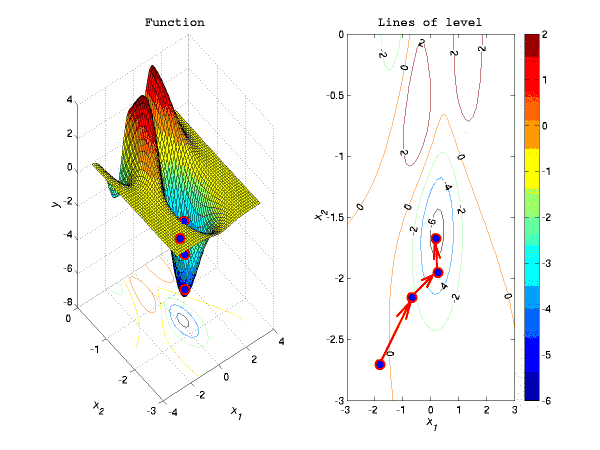
descent method's schema
Рис.4.1 — Схема работы методов спуска

Вверх

Выводы


В данной работе были кратко рассмотрены основные классы оптимизационных задач, выделены их особенности и рассмотрены подходы, позволяющие находить их решения. Также здесь приведен краткий обзор алгоритмов оптимизации, существующего оптимизационного ПО и литературы по данной тематике. На текущий момент в рамках работы разработаны и внедрены в моделирующую среду Diana интерфейсы основных оптимизационных задач и решателей данных задач. Был дополнительно реализован простой градиентный алгоритм алгоритм с модификацией Армихо [9], но в связи с тем, что данный алгоритм не справлялся с решением плохо масштабированных задач, от дальнейших исследований в данном направление пришлось отказаться. Вместо этого в моделирующую среду Diana мной был имплементирован код LBFGS-B-алгоритма, разработанный П.Лу [7].

В дальнейшем планируется на языке C++ реализовать модифицированный LBFGS-B-алгоритм и исследовать эффективность предложенной модификации на реальных моделях с использованием как подхода с оценкой начальной точки, так и ММС, а также исследовать один из алгоритмов минимизации квадратов нелинейных функций.

Вверх

Список использованной литературы


  1. Nocedal, Jorge; Wright, Stephen J. Numerical optimization. — New York, NY [u.a.]: Springer, Springer series in operations research, 1999. — 623 с.
  2. Измаилов, А.Ф.; Солодов, М.В. Численные методы оптимизации. — М.: «ФИЗМАТЛИТ», 2003. — 304 с.
  3. Бертсекас, Д. Условная оптимизация и методы множителей Лагранжа. — М.:Радио и связь, 1987. — 400 с.
  4. Сухарев, А.Г.; Тимохов, А.В.; Фёдоров, В.В. Курс методов оптимизации. — М.: Наука, 1986. — 328 с.
  5. More, Jorge J.; Wright, Stephen J. Optimization software guide. — Philadelphia, Pa.: SIAM Soc. for Industrial and Applied Mathematics, 1994. — 154 с.
  6. Peifer, M.; Timmer, J. Parameter estimation in ordinary differential equations using the method of multiple shooting — a review. — Freiburg: Freiburg Centre for Data Analysis and Modelling, 2005
  7. Byrd, Richard H.; Lu,P.; Nocedal, Jorge; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. — Northwest university, 1994
  8. Horbelt, Werner Maximum likelihood estimation in dynamical systems. — Freiburg: Albert—Ludwigs—Universitaet Freiburg Fakultaet fuer Physik, 2001.
  9. Polak, Elijah Optimization : algorithms and consistent approximations (Applied mathematical sciences; v.124). — New York, NY [u.a.] : Springer, 1997. — 779 с.
  10. Censor, Yair; Zenios, Stavros Andrea Parallel optimization : theory, algorithms, and applications — New York, NY [u.a.] : Oxford Univ. Press, 1997. — 539 с.
  11. Сеа, Ж. Оптимизация. Теория и алгоритмы. — М.: «Мир», 1973. — 244 с.
  12. Retout, Sylvie; Mentre, France; Bruno, Rene Fisher information matrix for non-linear mixed-e ects models: evaluation and application for optimal design of enoxaparin population pharmacokinetics. — Sylvie Retout, INSERM U436, CHU Pitie Salpetriere, 91 bd de l Hopital, 75013 Paris, France, May 2001. — 15 с.
  13. Bock, Hans Georg; Koerkel, Stefan; Kostina, Ekaterina; Schloeder, Johannes P. Methods of Design of Optimal Experiments with Application to Parameter Estimation in Enzyme Catalytic Processes. — Interdisciplinary Center for Scientific Computing (IWR), University of Heidelberg, Im Neuenheimer Feld 368, 69120 Heidelberg, Germany, October 2004. — 25 с.
  14. Kutalik, Zoltan; Cho, Kwang-Hyun; Gordon, Steve V.; Wolkenhauer, Olaf Optimal Sampling Time Selection for Parameter Estimation in Dynamic Pathway Modelling. — Control Systems Centre, Department of Electrical Engineering and Electronics, UMIST, Manchester, UK, — 2003. — 22 с.
  15. Broyden, C. G. Journal of the Institute of Mathematics and Its Applications.#6. — 1970. — 76-90 с.
  16. Fletcher, R. Computer Journal.#13. — 1970. — 317 с.
  17. Goldfarb, D. Mathematics of Computation.#24. — 1970. — 23 с.
  18. Shanno, D. F. Mathematics of Computation.#24. — 1970. — 647 с.
  19. Walter, Eric ; Pronzato, Luc Identification of parametric models from experimental data. — London: Springer, 1997. — 403 с.
  20. Schittkowski, Klaus Numerical data fitting in dynamical systems: a practical introduction with applications and software . — Dordrecht [u.a.] : Kluwer, 2002. — 392 с.
  21. Nocedal, Jorge Mathematics of Computation.(Updating quesi-Newton matrices with limited storage.)#35 — 1980, — 773-782 с.
Вверх

Разработал Sergiy Gogolenko (Май 2006)