Реферат

Введение

Проблема разбиения графов возникает во многих научно-технических задачах, решение которых можно частично или полностью свести к решению на графовых структурах. К классу таких задач традиционно относят задачи математической физики на неструктурированных сетках, проблему балансирования загрузки распределенных вычислительных систем, проблему девиртуализации решения задачи на реальной параллельной ЭВМ и другие. Как правило, целью разбиения является получение независимых подмножеств вершин исходного графа с минимальным количеством связей между этими подмножествами. Формально это можно записать следующим образом:

Мы имеем граф G=(V,E), где V - это множество вершин графа, а Е - множество его ребер. Количество вершин |V| равно n. Необходимо получить такое разбиение графа на p частей V1,V2,...,Vp, чтобы для всех пар i,j = 1,2,…,p и i <> j выполнялись следующие условия:

• пересечение Vi c Vj = 0
• объединение всех подмножеств Vi = V
• количество вершин в каждом разделе |Vi|=n/p, если требует условие задачи
• количество ребер множества | с начальной вершиной va из Vi и конечной вершиной vb из Vj | было минимальным среди всех возможных разбиений V.

Для облегчения понимания, задача разбиения представлена ниже на анимации:

разбиение графа на 4 части

При разработке алгоритмов разбиения основной проблемой, с которой встречается разработчик, является баланс между количеством вариантов перебора и трудоемкостью алгоритма. Во многих задачах недостаточно просто разбить граф на части, а сделать это необходимо за кратчайшее время, так как разбиение является всего лишь промежуточным этапом решения. Поэтому полный перебор вариантов разбиения для больших графов на практике не применим в связи с NP-полнотой и соответственно неудовлетворительным временем выполнения. Вместо этого используются методы с частичным перебором и применением разнообразных схем для последовательного улучшения качества разбиения. Качество разбиения определяется такими важными показателями как количество связей между частями разбитого графа, величина веса каждой из частей и другими, в зависимости от решаемой проблемы.

Существующие решения данной проблемы

На данный момент существует довольно много последовательных и параллельных алгоритмов (геометрические, спектральные, многоуровневые) разбиения графов, которые были реализованы в конкретных программных продуктах. Самыми распространенными программными продуктами из этой серии являются METIS [1] и ParMETIS [2], которые были разработаны в университете Миннесоты в 1998-2003 годах. В этих программных продуктах реализован класс так называемых многоуровневых алгоритмов, которые показали довольно хорошие результаты по скорости работы и качеству создаваемых разделов. Рассмотрим подробнее суть многоуровневой методики решения данной проблемы.

Многоуровневый алгоритм разбиения состоит из трех этапов ([3], [4], [5]):

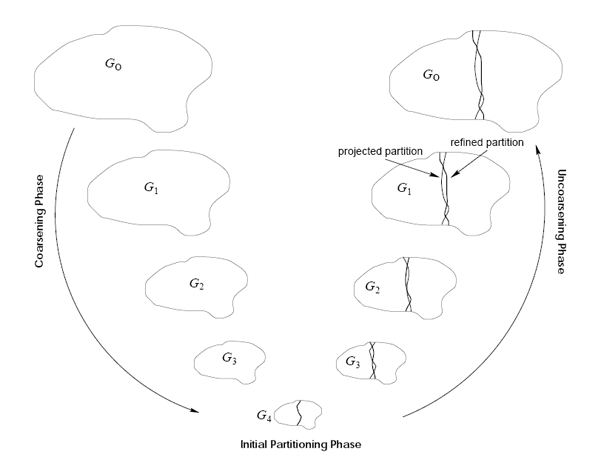
Многоуровневый алгоритм разбиения

• минимизация графа до нескольких сотен вершин (coarsening-стадия);
• разбиение графа на заданной количество частей;
• развертывание разбитого графа до первоначального размера (uncoarsening - стадия) с одновременной минимизацией связей между разделами.

Минимизация графа Во время минимизации графа последовательно получают из графа Gi=(Vi-1,Ei-1) меньший производный граф Gi=(Vi,Ei), причем |Vi|<|Vi-1|, где i – уровень минимизации, а |Vi| и |Vi-1| - множество вершин графа на одном из этапов минимизации. Принцип минимизации графа заключается в следующему: набор инцидентных вершин объединяется в одну при следующем уровне минимизации. Причем вес минимизированной вершины равняется сумме весов вершин, которые объединились в минимизированную. Связность минимизированной вершины тоже равняется сумме связностей первоначальных вершин. Минимизация графа завершается, когда количество вершин |Vi| в производном графе достигает значения, меньше 100.

Разбиение графа Для разбиения минимизированного графа разработчиками предусмотрено четыре различных алгоритма разбиения на части: спектрального деления пополам (spectral bisection), деления пополам Кернигана-Лина (Kernighan-Lin bisection), роста регионов в ширину (breadth-first region growing) и "жадного" роста регионов (greedy region growing).

Развертывание графа В процессе данного этапа выполняется последовательное развертывание вершин в разделах до первоначальных размеров. При этом на каждом этапе увеличения используется один из алгоритмов локального улучшения, которые базируются на алгоритме Кернигана-Лина (Kernighan-Lin Refinement). Пары вершин, которые имеют больше внешних связей с противоположным разделом, чем внутренних (внутри раздела), обмениваются местами. На этом улучшение на i-м уровне заканчивается, и выполняется переход на следующий i-1 уровень, и т.д.

Текущие результаты

На данный момент мной продолжается работа по данной теме, которая завершится в январе 2007 года. К текущим результатам можно отнести три программы, разработанные мной:

• для генерации ориентированных цикличных графов, которые отвечают требованиям электронных схем
• для преобразования описания полученного графа в формат METIS
• для визуализации графов и разделов, созданных библиотекой METIS, на базе утилит приложения GraphViz.

Результаты совместной работы моих приложений с библиотекой METIS и приложением GraphViz представлены на нижеследующих рисунках:

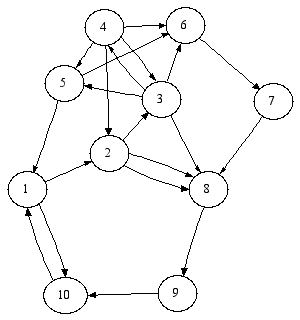
Cгеннерированный граф G(10, 20)

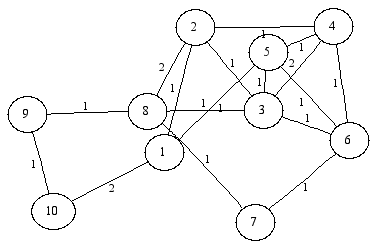
Преобразованный граф в формат библиотеки METIS

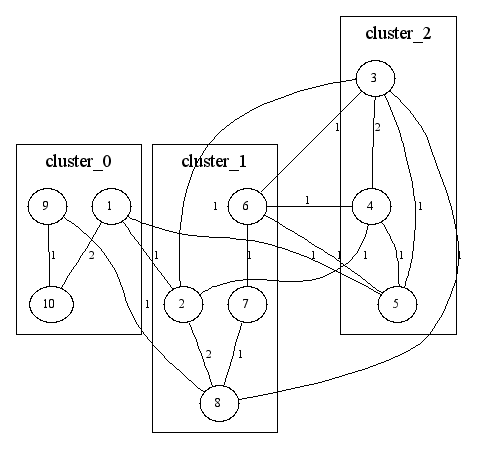
Полученный граф, в результате разбиения библиотекой METIS на три части

Заключение

Проблема разбиения графов является актуальной при решении многих научных задач. В наше время существует много классов алгоритмов разбиения и каждый класс алгоритмов имеет много разновидностей. В данном реферате основное внимание уделено рассмотрению так называемого многоуровневого метода разбиения графов, на котором основываются программные продукты METIS и ParMETIS (последовательная и параллельная реализация данного метода соответственно).

Список литературы

[1] George Karypis and Vipin Kumar,  METIS - A Software Package for Partitioning Unstructured Graphs, Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices

[2] George Karypis, Kirk Schloegel and Vipin Kumar, ParMETIS - Parallel Graph Partitioning and Sparse Matrix Ordering Library

[3] George Karypis and Vipin Kumar - Analysis of Multilevel Graph Partitioning

[4] George Karypis, Kirk Schloegel and Vipin Kumar - Graph Partitioning for High Performance Scientific Simulations

[5] George Karypis and Vipin Kumar - A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs

Наверх