Тема выпускной работы магистра:

Исследование методов многокритериальной оптимизации для оценки и выбора партнеров для предприятий оптовой торговли

1.1 Актуальность

В задачах математического программирования с одним критерием нужно определить значение целевой функция, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, мы практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу. Покажем, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев.

Методы решения задач математического программирования с одним критерием интенсивно разрабатывались последние 60 лет. Изучение таких методов, однако, отражало самый ранний и простой этап в развитии математического программирования. По мере того как мы постепенно вступаем в век информатики, становится ясно, что практически любая серьезная реальная задача характеризуется больше чем одним критерием. Лица, принимающие решения (ЛПР), в значительно большей степени, чем когда бы то ни было, ощущают необходимость оценивать альтернативные решения с точки зрения нескольких критериев.

Результаты исследования задач планирования и управления показывают, что в реальной постановке эти задачи являются многокритериальными. Так, часто встречающееся выражение «достичь максимального эффекта при наименьших затратах» уже означает принятие решения при двух критериях. Функционирование предприятий обладает большим спектром характеристик, поэтому определение его будущих параметров является весьма важным в отношении перспективности производства. Такие задачи часто встречаются на предприятиях, находящихся в кризисном состоянии, и необходимость выбора партнеров с соответствующими параметрами может являться основной при определении стратегии и тактики для определенного предприятия. Это позволит повысить эффективность функционирования предприятия, что может привести к росту объемов реализации и улучшению его финансового состояния по всем показателям.

Таким образом, для эффективного решения любой из данных задач необходимо в первую очередь построить многокритериальную математическую модель, которую затем нужно оптимизировать, предварительно выбрав наиболее подходящий для этого метод.

Одной из наиболее важных особенностей прикладных задач выбора является нечеткий характер критериев выбора альтернатив, их параметров, ограничений, накладываемых на возможность выбора тех или иных вариантов и т.д. Вследствие этого, во многих случаях оказывается невозможным построение адекватной математической модели исследуемой проблемы, что влечет за собой необходимость использования экспертных оценок, которые часто оказываются единственной информацией для принятия решений. Естественно, возникает необходимость разработки методов, позволяющих эффективно получать и обрабатывать нечеткую экспертную информацию.

Объектом исследования являются методы многокритериальной оптимизации.

Цель работы – изучение алгоритмов и математических принципов решения многокритериальных задач выбора и рассмотрение наиболее распространенных и эффективных из них для оптимизации выбора партнеров для предприятий оптовой торговли.

Имеется предприятие, торгующее оптом сельскохозяйственными товарами. Проблема состоит в том, что у предприятия много клиентов, некоторые из них совершают много больших покупок, однако значительно задерживают оплату, а другие наоборот платят вовремя, однако их заказы малы.

Требуется оценить клиентов, проранжировать их, и на этом основании установить систему скидок, при этом будут учитываться количество заказов, их сумма, долг, оплата и длительность сотрудничества.

Предполагается применение аппарата многокритериальной оптимизации к конкретному процессу осуществления торговых операций с оптимизацией его параметров. При этом планируется построение многокритериальной математической модели процесса и решение задачи многокритериального программирования применительно к данной модели. Оптимизацию планируется проводить с использованием программного обеспечения, которое также будет нами разработано в соответствии с примененным методом оптимизации. Оптимизация будет проводиться по методам, рассмотренным ниже в данной работе.

Проблема принятия решений или проблема выбора вариантов является одной из самых распространенных задач, возникающих практически во всех сферах деятельности: технической, экономической, социальной и т.д.

Данная работа посвящена рассмотрению проблемы оценки партнеров предприятий с применением методов многокритериальной оптимизации. Это будет реализовано в программном продукте, на основании базы данных, учитывая семь выделенных критериев. Для анализа используются данные о закупках за два года, при этом имеется примерно 250 покупателей и 2000 записей.

Поскольку данная постановка задачи выделяет несколько функций цели, необходимо для ее решения применить методы многокритериальной оптимизации. В первую очередь следует построить многокритериальную математическую модель, которую затем нужно оптимизировать, предварительно выбрав наиболее подходящие для этого методы.

Существует много различных методов многокритериальной оптимизации. Все они делятся на 2 категории: на конечном и непрерывном множестве альтернатив. В данном случае имеется конечное количество покупателей, то есть конечное множество альтернатив.

Подходы для решения задач на конечном множестве альтернатив, при помощи которых будет решаться поставленная задача, включают следующие методы: выбор по абсолютному предпочтению, метод главного критерия, построение линейной свертки, построение множества эффективных решений (недоменируемых), выбор лучшего по правилу большинства.

Вначале строим математическую модель вида:

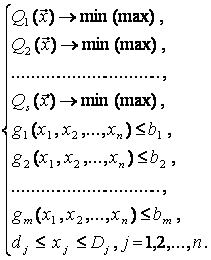
Выделение множества критериев

Длительность сотрудничества, дн .--> max ; количество дней с момента первой покупки.

Количество заказов, шт. --> max; то сколько раз производились закупки.

Средний объем закупок, грн. --> max.

Средний процент оплаты , % --> max; средний процент оплаченной суммы на момент покупки, т.е. какой процент был оплачен сразу .

Сумма долга на момент покупки, грн. --> min; сумма долга на момент покупки, сумма денег, которую предприятие сразу не оплатило .

Сумма закупок, грн. --> max; суммарный объем закупок.

Финансовое положение, балл. (1-100) --> max; экспертные бальные оценки.

Для начала произведем переход к бальным показателям, чтобы привести их к единой шкале и сделать все на максимум. Для перехода к баллам используем метод пересчета диапазона значений: Выбирается шкала от 1 до 100 баллов, а потом попарно пересчитываются показатели.

Выбор по абсолютному предпочтению: выбираются наилучшие варианты по всем показателями. Если никакой вариант не удовлетворяет всем показателям, то решение найти нельзя, это стандартная ситуация для многокритериальных задач.

Согласно методу абсолютного предпочтения результат получаем в таком виде: по каждому критерию выбираем лучшие варианты. В программе получаем списки лучших вариантов для каждого критерия.

Выбор главного критерия: один критерий выбирается главным, а по остальным устанавливаются ограничения. То решение считается лучшим, которое удовлетворяет ограничениям и является лучшим по главному критерию.

В программе по методу главного критерия получаем список ответов, которые упорядочены от лучшего к худшему.

Выбор лучшего по правилу большинства: по каждому показателю некоторое пороговое значение по каждому частному критерию; для каждого варианта считается количество показателей, превышающих порог для максимумов, а для минимумов – не превосходящих порог; лучшим считается решение с максимальным значением количества таких показателей.

По правилу большинства получаем список ответов удовлетворяющим ограничениям.

Согласно результатам метода главного критерия и правило большинства можно разработать систему скидок. Пользователь устанавливает максимальную и минимально возможную скидку, выбирает метод и устанавливает параметры метода. Согласно полученным решениям скидка распределятся равномерно: максимальная – самому лучшему, минимальная – самому худшему.

Построение множества эффективных решений (недоменируемых или множество Парето): получаем список предприятий, для которых нельзя однозначно по всем критериям сказать, какое из них лучше.

Построение линейной свертки предусматривает суммирование баллов по всем критериям для каждого предприятия. Таким образом, получаем упорядоченный список предприятий, каждое из которых имеет свой суммарный балл. Ответом будет предприятие с максимальным баллом, а проранжированный список предприятий будет применяться для построения системы скидок.

Построение системы скидок по результатам линейной свертки будет иметь вид: пользователь будет задавать максимально возможную и минимально возможную скидку, а также количество предприятий, которым будут даны скидки. Согласно полученным решениям скидка распределятся равномерно: максимальная – самому лучшему, минимальная – самому худшему.

Наиболее понятно это будет видно на анимации:

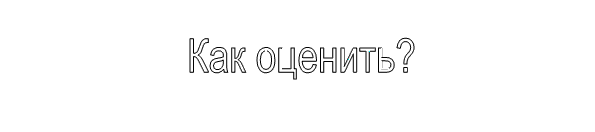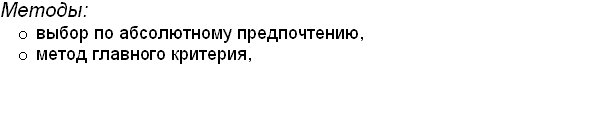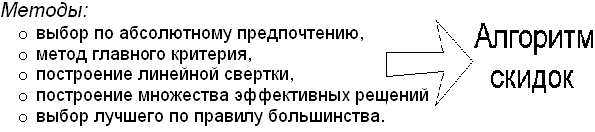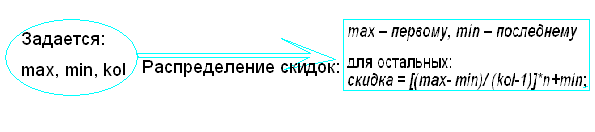
Анимированное изображение. Формат: gif. Размер: 53 КБ. Количество слайдов: 14. Количество повторений: 12. Скорость смены слайдов: 1слайд/секундa

Алгоритм системы скидок

1. Задается: % max и min скидки, kol - количество предприятий, которым будет скидка.

2. Выбирается метод:

o Метод главного критерия

o Выбор лучшего по правилу большинства

o Ранжирование партнеров

3. Получаем упорядоченный список ответов согласно работе метода, не более указанного kol.

4. Распределение скидок:

max – первому, min – последнему

для остальных:

[(max- min)/ (kol-1)]*n+min

Проводим несколько тестирований разработанных методов при помощи написанной программы, анализируем результаты и обобщаем результаты исследования, вносим рекомендации по дальнейшим разработкам.

Поскольку моя тема довольно актуальна, то многие выпускники ДонНТУ ее разрабатвывали, ссылки на их работы можно найти в перечне ссылок.

Украинские институты также занимались разработками по данной тематике, что также отмечено в перечне ссылок.

В процессе анализа и поиска иностранных разработок, чаще всего мне приходилось сталкиваться со следующими институтами:

1) National Science Foundation (USA)

Это независимое федеральное агентство, созданное в 1950 году. Занимается поддержкой многих университетов и колледжей в отраслях математики, компьютерной науки. Поддерживает отрасли фундаментальной науки и инжиниринга, а также занимается новыми разработками.

2) Institute of information technologies – BAS (Bulgarian Academy of Sciences)

Эта Болгарская академия наук занимается компьютерным моделированием, комплексным анализом. Ее сотрудники написали много полезных научных работ

3) Institute of Electrical and Electronics Engineers (IEEE)

Мировая лидирующая организация по технологиям. Это волонтерская организация. Объединяет авторов из различных уголков мира в области компьютерной, телекоммуникационной, электронных разработок. Члены организации обмениваются своими профессиональными исследованиями, делятся новыми разработками

3.1 Выполненные разработки и исследования

Решение проблемы оценки партнеров предприятий с применением методов многокритериальной оптимизации, будет реализовано в программном продукте, на основании базы данных, учитывая семь выделенных критериев. Для анализа используются данные о закупках за два года, при этом имеется примерно 250 покупателей и 1500 записей. Сводная таблица, с выделенными критериями по всем предприятиям показана на рис.1.

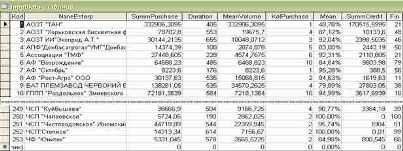
Рис.1 Критерии в базе данных

Применяемые методы: абсолютное предпочтение, метод главного критерия, линейная свертка, множество эффективных решений, правило большинства.

Переход к баллам

Показатели должны быть в единой шкале и все на максимум.

Используем метод пересчета диапазона значений:

1. Выбирается шкала от 1 до 100 баллов.

2. Ищем max и min по каждому показателю.

3. Рассчитываем значение по формуле:

1балл= (max – min)/99

Бальное значение = (значение – min)/1балл+1

Если показатель на минимум:

Бальное значение = (max – значение)/1балл+1

Переход к баллам реализуется в прогрмме, что показано на рис.2.

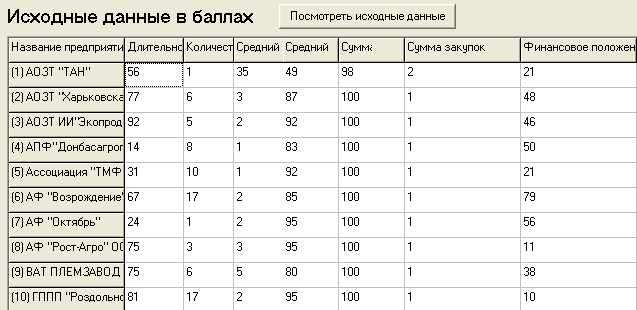
Рис.2 Исходные данные в баллах

Выбор по абсолютному предпочтению

Выбираются наилучшие варианты по всем показателями (т.е. с max баллами). Результат программной реализации на рис.3

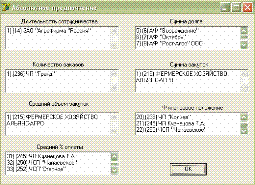
Рис.3 Абсолютное предпочтение

Метод главного критерия

1. Выбираем главный критерий.

2. По остальным устанавливаем ограничения.

3. Решение - лучшее, которое удовлетворяет ограничениям и лучшее по главному критерию.

Результат программной реализации на рис.4

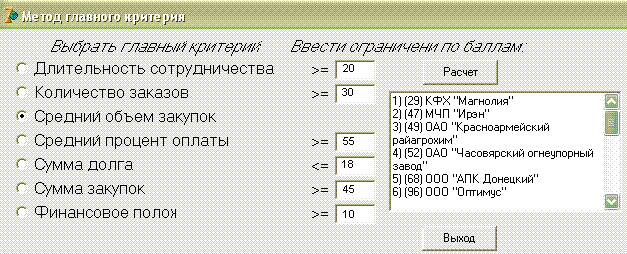
Рис.4 Метод главного критерия

Выбор лучшего по правилу большинства

1. Устанавливаем пороговое значение по каждому критерию.

2. Для каждого предприятия считается количество показателей, удовлетворяющих условиям.

3. Лучшее решение - с максимальным количеством показателей.

Результат программной реализации на рис.5

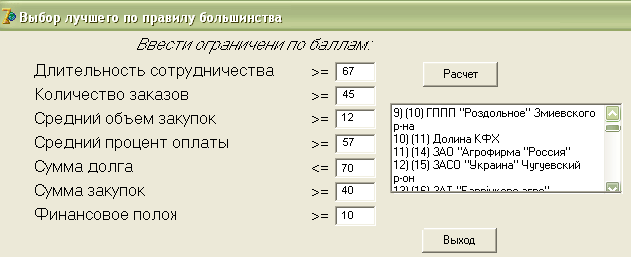
Рис.5 Выбор лучшего по правилу большинства

Построение линейной свертки

Суммируем баллы для каждого предприятия по формуле:

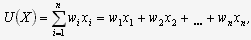
где: wi – вес (важность) i-го критерия, назначаемый ЛПР; xi – оценка альтернативы X по i-му критерию.

Получаем упорядоченный список предприятий, каждое из которых имеет свой суммарный балл. Ответом будет предприятие с максимальным баллом. Проранжированный список предприятий будет применяться для построения системы скидок.

В данной работе были подробно рассмотрены существующие проблемы и пути их решения при помощи методов многокритериальной опитимизации. Некоторые из методов были реализованы программно.

В дальнейшем проведем несколько тестирований разработанных методов при помощи написанной программы, проанализируем результаты и обобщим результаты исследования, внесем рекомендации по дальнейшим разработкам.

В настоящий момент работа в процессе разработки. Ожидается доработка к декабрю 2007 года. С вопросами по поводу диссертации обращаться к автору.

Литература