Автор: Л.П. Фельдман, д-р техн. наук
Донецкий национальный технический университет
Украина, 83001, Донецк, ул. Артема, 66.
тел. (062)3010856, e-mail: feldman@r5.dgtu.donetsk.ua
Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами
Введение
Доклад содержит обобщение результатов исследований [1,2,3,5], посвященных параллельным методам численного решения задачи Коши для системы обыкновенных дифференциальных уравнений и является продолжением ранее опубликованных работ [6,7,8,9,10]. В нем приводится доказательство сходимости приближенного решения для m- шаговых k точечных блочных методов, что представляет обобщение ранее опубликованных результатов. В [7] приведено доказательство сходимости для одношаговых k точечных, а в [9] –для многошаговых многоточечных методов при k=m Рассмотрены также и методы оценки локальной погрешности решения блочными разностными схемами и даны практические рекомендации их использования для более широкого набора параллельных разностных схем.
1. Параллельные вычислительные схемы многошаговых блочных методов
Для упрощения изложения рассмотрим вначале решение задачи Коши для одного обыкновенного дифференциального уравнения первого порядка.
x" = f(t,x), x(t0) = x0 (1)

Рис. 1. Схема разбиения на блоки для одношагового k-точечного метода
блочными методами. Множество M точек равномерной сетки {tm},
![]() и tM = T с шагом τ разобьем на N блоков, содержащих k точек каждый, при этом kN£M. В каждом блоке введем номер точки
и tM = T с шагом τ разобьем на N блоков, содержащих k точек каждый, при этом kN£M. В каждом блоке введем номер точки
![]() и обозначим через tn,i точку n блока с номером i. Точку
и обозначим через tn,i точку n блока с номером i. Точку
 назовём началом блока n, а
назовём началом блока n, а
 – концом блока. Очевидно, что имеет место tn,k = tn+1,0. Условимся начальную точку t0 в блок не включать. При численном решении задачи Коши для каждого следующего блока новые k значений функции вычисляются одновременно. Поэтому блочные методы особенно удачно реализуются на параллельных вычислительных системах [1].
– концом блока. Очевидно, что имеет место tn,k = tn+1,0. Условимся начальную точку t0 в блок не включать. При численном решении задачи Коши для каждого следующего блока новые k значений функции вычисляются одновременно. Поэтому блочные методы особенно удачно реализуются на параллельных вычислительных системах [1].
Различают два типа блочных методов: одношаговый блочный метод m=1 и многошаговый блочный метод 1 < m. В первом методе только значение в последней точке предшествующего блока используется для вычислений приближенных значений в следующем блоке, тогда как во втором методе используются все или несколько точек предшествующего блока.
Пусть un,0 – приближенное значение решения задачи Коши (1) в точке tn,0 – начальной точке обрабатываемого блока. Предполагается, что в пределах одного блока точки сетки находятся на равных расстояниях: tn,i = tn + iτ, i = 1,…,k В общем случае уравнения многошаговых разностных методов для блока из k точек при использовании вычисленных значений приближенного решения в m предшествующих блоку узлах, с учетом введенных выше обозначений можно записать в виде:
![]() ,
,
![]() ,
,
![]() , (2)
, (2)
где
![]() .
.
Формулы (2) определяют m-шаговый k-точечный разностный метод.
Для одношаговых разностных методов разностные уравнения имеют вид:
![]() ,
,
![]() ,
,
![]() (3)
(3)
Формулы (3) определяют одношаговый k-точечный разностный метод. Определить коэффициенты ai,j и bi,j формул (2) и (3) можно интегро-интерполяционным методом. Построим интерполяционный многочлен Lm+k–1(t) с узлами интерполяции i = –m – 1, m – 2,…,0, 1, k и соответствующим им значениям правой части уравнения (1) Fn,i = f(tn,i, un,i). Проинтегрировав его в пределах (tn, tn + iτ),
![]() ,
,
 ,
,
получим уравнения (2) для выбранных m и k Например, формулы для двухточечного двухшагового метода имеют вид
un,1 = un –
![]() τ( F-1+n,1 – 13Fn,0 – 13Fn,1 + Fn,2)
τ( F-1+n,1 – 13Fn,0 – 13Fn,1 + Fn,2)
un,2 = un –
![]() τ (Fn,0 + 4Fn,1 + Fn,2)
τ (Fn,0 + 4Fn,1 + Fn,2)
2. Погрешность аппроксимации блочных методов.
Выражения для невязoк m-шагового k-точечного разностного метода (2) на решении x(t) исходного дифференциального уравнения имеют вид
![]() (4)
(4)
где
![]() .
.
Разлагая
![]() и
и
![]() в ряды Тейлора в окрестности точки tn, получим
в ряды Тейлора в окрестности точки tn, получим
![]()
![]()
![]()
Подставляя эти разложения в выражение (4) для невязки, будем иметь
 (5)
(5)
Сгруппируем члены с одинаковыми производными и изменим порядок суммирования в последнем выражении, тогда получим
 (6)
(6)
Отсюда следует, что погрешность аппроксимации имеет порядок p, если выполнены условия
 (7)
(7)
Система уравнений (7) для каждого фиксированного i содержит p уравнений и k+m неизвестных ai,j,
![]() и bi,j, i,
и bi,j, i,
![]() . Положим, чтобы p = k + m, тогда из системы (7) при фиксированном i можно будет определить неизвестные коэффициенты bi,j,
. Положим, чтобы p = k + m, тогда из системы (7) при фиксированном i можно будет определить неизвестные коэффициенты bi,j,
![]() и ai,j,
и ai,j,
![]() . Поступая аналогично для каждого
. Поступая аналогично для каждого
![]() , определим все неизвестные коэффициенты bi,j,
, определим все неизвестные коэффициенты bi,j,
![]() и ai,j, i,
и ai,j, i,
 , которые в дальнейшем будем считать элементами матриц А и В соответственно. Отсюда следует, что наивысший порядок аппроксимации m-шагового k-точечного блочного метода равен m + k. Его погрешность в соответствии с (6) определяется формулой
, которые в дальнейшем будем считать элементами матриц А и В соответственно. Отсюда следует, что наивысший порядок аппроксимации m-шагового k-точечного блочного метода равен m + k. Его погрешность в соответствии с (6) определяется формулой
![]() (8)
(8)
Элементы
![]() матриц Bи A можно найти, решая систему (7) для любых заданных k и m.
матриц Bи A можно найти, решая систему (7) для любых заданных k и m.
3. Сходимость и оценка погрешности многошаговых блочных методов.
Обозначим через: un – вектор значений приближенного решения в точках n-го блока с компонентами un,i, i = 1, 2, …, k; u"n – вектор, компонента u"n,i = f(tn,i, un,i),
![]() которогоравна значению правой части уравнения (1) в точке n-го блока, соответствующей значению приближенного решения; v"n-1 – вектор, компонента v"n-1,j = f(tn-1, j, un-1,j),
которогоравна значению правой части уравнения (1) в точке n-го блока, соответствующей значению приближенного решения; v"n-1 – вектор, компонента v"n-1,j = f(tn-1, j, un-1,j),
![]() которого равна значению правой части уравнения (1) в точке (n-1)-го блока (если k ≥ m), соответствующей значению приближенного решения.
которого равна значению правой части уравнения (1) в точке (n-1)-го блока (если k ≥ m), соответствующей значению приближенного решения.
Запишем систему (2) в векторной форме
D-1(un – un,0e) / τ = Bv"n–1 + Au"n, (9)
где D = (dii) – диагональная матрица с элементами dii = i, i = 1, 2, …, k, B – матрица с элементами bi,j,
![]() ,
,
![]() , A – матрица с элементами ai,j, i,
, A – матрица с элементами ai,j, i,
![]() , e – единичный вектор-столбец
, e – единичный вектор-столбец
Обозначим через xn – вектор значений точного решения задачи (1) в точках tn блока n. Получим уравнение, которому удовлетворяет вектор zn = un – xn погрешностей в блоке. Подставим в левую часть уравнения (9) un = zn + xn добавим к правой части и вычтем из нее выражение By"n–1 + Ax"n, где y"n–1,i = f(tn–1, xn–1, i)
 . Тогда уравнение для погрешности примет вид
. Тогда уравнение для погрешности примет вид
D-1(zn – zn,0e) / τ = – D-1(xn – xn,0e) / τ +By"n–1 + Ax"n +B(v"n-1 – y"n–1) +A(u"n – x"n).
Входящее в правую часть выражение
rn=–D-1(xn – xne) / τ + By"n–1 + Ax"n (10)
представляет собой вектор невязок разностных уравнений (9) на точном решении уравнения (1). Поскольку разностные уравнения (9) аппроксимируют исходное уравнение (1) в точках блока с порядком O(τk+m), то имеет место оценка
||rn|| = O(τk+m). (11)
Оставшиеся члены правой части уравнения для погрешности обозначим через
ωn = B(v"n–1 – y"n–1) +A(u"n – x"n). (12)
Тогда уравнение для погрешности запишется короче
zn = zn,0e + τD(rn – ωn). (13)
Вектор-функция ωn зависит нелинейно от погрешности zn. Вид этой зависимости определяется функцией f(t, x). В дальнейшем будем предполагать, что f(t, x) удовлетворяет условию Липшица по второму аргументу, т.е.
|f(t, x1) – f(t, x2)| ≤ L|x1 – x2| (14)
для всех t, x1, x2 из рассматриваемой области. Согласно формуле конечных приращений Лагранжа для соответствующих компонент имеем
u"n,i – x"n,i = f(tn,i, un,i) – f(tn,i, xn,i) = ln,i zn,i, i =
![]()
v"n–1,i – y"n–1,i = f(tn–1,i, un–1,i) – f(tn–1,i, xn–1,i) = ln–1,i zn–1,i, i =
![]()
где
ln,i = fx(tn,i, xn,i + θzn,i), 0 < θ <1, i =
![]() ,
,
ln–1,i = fx(tn–1,i, xn–1,i + ηzn–1,i), 0 < η <1, i =
![]() .
.
Подставляя последние в (12), получим
ωn = BDm
![]() n–1 + ADk zn,
n–1 + ADk zn,
где
 = v"n-1 – y"n–1, Dm – диагональная матрица с элементами dmi,i = ln–1,i, i =
= v"n-1 – y"n–1, Dm – диагональная матрица с элементами dmi,i = ln–1,i, i =
![]() и Dk – диагональная матрица с элементами dki,i = ln,i.
и Dk – диагональная матрица с элементами dki,i = ln,i.
Для норм матриц в силу (14) справедливы следующие оценки
||Dm|| ≤ L, ||Dk|| ≤ L (15)
Заменим ωn в уравнении (13) полученным для него выражением, запишем его в виде
zn = zn,0e + τDrn + τDBDm
 n–1+ τDADkzn
n–1+ τDADkzn
Введем норму ||zn|| =
![]() |zn,i|. Далее, учитывая (11) и (15) и то, что для
|zn,i|. Далее, учитывая (11) и (15) и то, что для

![]() =
=
![]() |zn–1,k–m+i|
|zn–1,k–m+i|
 || zn–1||, получим неравенство
|| zn–1||, получим неравенство
||zn|| ≤ Сτk+m+1 + (1 + kτ||B||)||zn–1|| + τkL||A||||zn||,
которое преобразуем к виду
(1 – τkL||A||)||zn|| ≤ Сτk+m+1+ (1 + kτ||B||)||zn–1||.
Если на τ наложить ограничение
τ < τ0 =
![]() , (16)
, (16)
то оценка, связывающая нормы погрешностей соседних блоков, примет вид
||zn|| ≤ {Сτk+m+1+ (1 + kτ||B||)||zn–1||} /(1 – τkL||A||) , (17)
т.к. в силу условия (16) имеет место (1 – τkL||A||) > 0. Подставляя последовательно в (17) значения погрешностей для блоков n–1, n–2, …, 1, получим
 ≤
≤
 /
/
/ (1 – τkL||A||),
где ||z0|| =
![]() |zi| – норма погрешности приближенного решения, полученного каким-либо способом на начальном участке интегрирования для первых m узлов. Упростим последнее выражение
|zi| – норма погрешности приближенного решения, полученного каким-либо способом на начальном участке интегрирования для первых m узлов. Упростим последнее выражение
||zn|| ≤

Последнее неравенство справедливо для любого 0 < n ≤ N; из этого следует:
||zn|| ≤
![]() . (18)
. (18)
Таким образом, если правая часть уравнения (1) f(tx) удовлетворяет условию Липшица по второму аргументу с константой L и rn – невязка m-шагового k-точечного блочного метода (2), определенная согласно (18) с оценкой (11), то при
τ < τ0 =
![]() и τkn ≤ T
и τkn ≤ T
для погрешности метода имеет место оценка (18).
Следствие. Если разностное уравнение (2) аппроксимирует исходное уравнение (1) и
![]() , то решение разностной задачи (2) сходится при τ → 0 к решению исходной задачи (1), причем порядок точности совпадает с порядком аппроксимации (11).
, то решение разностной задачи (2) сходится при τ → 0 к решению исходной задачи (1), причем порядок точности совпадает с порядком аппроксимации (11).
4. Алгоритм решения разностных уравнений многошаговым блочным методом.
Итерационные формулы параллельного решения системы разностных уравнений многошагового многоточечного метода (2) для произвольного блока n получим, использовав (9):
uns+1 = une + τDBv"n–1+ τDA(u"n)s, s =
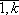 , (19)
, (19)
где s – номер итерации. По формуле (19) пересчитываются компоненты вектора приближенного решения uns+1, принадлежащие блоку n. При этом компоненты вектора
![]() , определенные в узлах предшествующего блока, сохраняют свои значения при этих вычислениях, а компоненты вектора
, определенные в узлах предшествующего блока, сохраняют свои значения при этих вычислениях, а компоненты вектора
![]() вычисляются вновь на каждой итерации. Чтобы начать решение m-шаговым разностным методом, необходимо определить каким-либо одношаговым разностным методом значения приближенного решения u0,i в первых m-1 точках, примыкающих к начальной точке t0 отрезка интегрирования. Таким образом будут определены значения компонент
вычисляются вновь на каждой итерации. Чтобы начать решение m-шаговым разностным методом, необходимо определить каким-либо одношаговым разностным методом значения приближенного решения u0,i в первых m-1 точках, примыкающих к начальной точке t0 отрезка интегрирования. Таким образом будут определены значения компонент
![]() вектора ν"0. Теперь следует задать исходное приближение для компонент
вектора ν"0. Теперь следует задать исходное приближение для компонент
![]() вектора u01, значения которых могут быть, например, найдены по m-шаговым формулам Адамса-Башфорта. В общем случае m-шаговые формулы Адамса-Башфорта для значений приближенного решения в узлах k-точечного блока на первой итерации в векторной форме могут быть записаны в виде
вектора u01, значения которых могут быть, например, найдены по m-шаговым формулам Адамса-Башфорта. В общем случае m-шаговые формулы Адамса-Башфорта для значений приближенного решения в узлах k-точечного блока на первой итерации в векторной форме могут быть записаны в виде
u1n = une + τB1v"n–1. (20)
Можно показать, что выполнение k шагов вычислений по формуле (19) обеспечит получение приближенного решения с локальной ошибкой порядка
![]() .
.
Приведем результаты решения следующей задачи Коши
x"= –10(t–1)x , x(0 )=1, (21)
трехшаговым четырехточечным методом с шагом t = 0.017.


a b
Рис 2. Графики приближенного решения уравнения (21) трехшаговым четырехточечным методом a и глобальной погрешности b
Поскольку точное решение задачи Коши известно, то сможем найти глобальную погрешность в каждой точке.
5. Методы с контролем на шаге.
Для оценки локальной погрешности при решении одношаговым многоточечным методом используем следующий подход. Решаются две задачи на одной сетке c одним и тем же шагом t:
первая – одношаговым k-точечным методом;
вторая – одношаговым (k+1)-точечным методом.
Второе решение необходимо для оценки локальной погрешности, поэтому основным является k-точечный метод. Используются значения приближенных решений в совпадающих k узлах основного блока. Лишняя k+1 точка является начальным приближением в расчетах решения в следующем блоке. Локальная погрешность приближенного решения одношаговым k-точечным методом в i-ом узле блока определяется формулой
un,i (k)– x(tn,i) ≈ φ(k+2)(tn,0, xn,0)τk+2, i =
![]()
и для (k+1)-точечного метода локальная погрешность в том же узле определяется формулой
un,i (k+1)– x(tn,i) ≈ φ(k+3)(tn,0, xn,0)τk+3, i =
![]() .
.
Вычитая из верхнего соотношения нижнее, получим представление главного члена погрешности k-точечного метода на шаге в виде
![]() (22)
(22)
который может быть использован для оценки локальной погрешности.
Для иллюстрации приведем оценки локальной ошибки, полученные по результатам решения задачи (21) с шагом t = 0.017, одношаговыми трехточечным (основное решение) и четырехшаговым методами (корректирующее решение). Оценка модуля пошаговой погрешности, полученная как разность решений одношаговыми трех- и четырехточечным блочными методами, и действительная локальная погрешности отличаются на величину порядка τ5, что обеспечивает надежность используемой оценки.


a b
Рис.3. Графики a- оценки локальной погрешности Etи b-глобальной погрешности Ep при решении задачи (21) одношаговым трехточечным методом
Из сравнения графиков, представленных на рис. 3, следует, что оценка локальной погрешности приближенного решения уравнения (21) трехшаговым четырехточечным методом меньше (в 15 раз) соответствующей накопленной погрешности. Это полностью согласуется с теоретическими оценками.
Для оценки локальной погрешности при решении многошаговым многоточечным методом используется аналогичный подход. Решаются две задачи на одной сетке c одним и тем же шагом t: первая – m-шаговым k-точечным методом; вторая – (m+1)-шаговым k-точечным методом. Второе решение используется для оценки локальной погрешности, поэтому основным является m-шаговый k-точечный метод. Оцениваются значения приближенных решений в совпадающих k узлах основного блока. Локальная погрешность приближенного решения m-шаговым k-точечным методом в i-ом узле блока определяется формулой
![]() (23)
(23)
а для (m+1)-шагового k-точечного метода локальная погрешность в том же узле определяется формулой
![]() (24)
(24)
Вычитая из (23) соотношение (24), получим представление главного члена погрешности одношагового k-точечного метода на шаге в виде
![]()
Таким образом, для главного члена погрешности получаем оценку
![]() (25)
(25)
Приведем оценку локальной погрешности gприближенного решения двухшаговым четырехточечным методом как разность соответствующих значений решений, полученных двухшаговым и трехшаговым четырехточечными методами.

Рис. 4. График оценки локальной погрешности при решении уравнения (21) двухшаговым четырехточечным методом.
В рассматриваемом случае оценка локальной погрешности приближенного решения двухшаговым четырехточечным методом практически совпадает со значениями накопленной погрешности. Таким образом, получается завышенная оценка локальной погрешности. Это можно объяснить тем, что решение трехшаговым четырехточечным методом с машинной точностью совпадает с точным решением задачи (21).
6. Заключение. Оценка эффективности блочных алгоритмов.
При численном решении задачи Коши для сравнительной характеристики методов можно рассматривать различные показатели. В случае произвольной правой части уравнения о трудоемкости метода естественно судить по числу обращений для вычисления значений правой части уравнения на каждый узел сетки. Для оценки эффективности одношаговых блочных методов найдем отношение времени выполнения алгоритма Рунге-Кутта на однопроцессорной ЭВМ ко времени выполнения одношагового блочного алгоритма соответствующего порядка на параллельной
ВС. Определим время выполнения алгоритма Рунге-Кутта
k+1 порядка точности на одном процессоре. Обозначим через tf– время вычисления значения функции f(tx), tad, tmul – время выполнения операции сложения и умножения соответственно. Время последовательного вычисления приближенных значений решения с точностью O(
![]() ) во всех k узлах блока составит
) во всех k узлах блока составит
Ts =k (k + 1)2 tf + k2 (tad + tmu).
Для параллельного выполнения вычислений по формулам (3) закрепим за каждым узлом блока процессор. При его реализации на k процессорах можно одновременно вычислять значения Fn,i,s,, а затем также одновременно получить по формулам (3) значения un,i,sдля каждого фиксированного s Объединим процессоры в кольцо, чтобы иметь возможность одновременной передачи данных соседним процессорам. Обозначим через tta– время передачи числа соседнему процессору. Время параллельного вычисления приближенных значений решения с той же точностью для всех узлов блока составит
Tp =( k+1)tf + k(tad + tmu) + k(k – 1)tta.
Ускорение параллельного одношагового k-точечного алгоритма можно будет теперь вычислить по формуле
W(k)= Ts / Tp.
Если учитывать только время вычислений правой части уравнения, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части, то ускорение k-точечного параллельного алгоритма можно считать приближенно равным
W(k)pot = k
Для оценки ускорения m-шагового k-точечного блочного метода сравним время его выполнения на мультипроцессорной системе со временем выполнения алгоритмаm-шагового метода Адамса-Башфорта на однопроцессорной ЭВМ. Метод Адамса-Башфорта можно рассматривать как многошаговый одноточечный блочный метод. Последовательное k-кратное применение формул Адамса-Башфорта позволяет вычислить приближенное решение в тех же k узлах блока, в которых параллельно за k итераций может быть вычислено решение
m-шаговым k-точечным блочным методом. В этом случае время вычисления будет приблизительно одинаково. Точность приближенного решения, полученного m-шаговым k-точечным блочным методом, имеет порядок
![]() , а точность приближенного решения, полученного по m шаговой формуле Адамса-Башфорта, имеет порядок
, а точность приближенного решения, полученного по m шаговой формуле Адамса-Башфорта, имеет порядок
![]() . Поэтому для получения решения с одинаковой точностью для метода Адамса-Башфорта надо выбрать шаг сетки мельче в
. Поэтому для получения решения с одинаковой точностью для метода Адамса-Башфорта надо выбрать шаг сетки мельче в
![]() раз, чем шаг для m-шагового k-точечного метода. Здесь M – число узлов сетки на отрезке решения задачи методом Адамса-Башфорта.
раз, чем шаг для m-шагового k-точечного метода. Здесь M – число узлов сетки на отрезке решения задачи методом Адамса-Башфорта.
Таким образом, ускорение параллельного m-шагового k-точечного алгоритма равно
W(mk)
![]() .
.
Аналогично могут быть получены оценки эффективности решения задачи Коши для системы обыкновенных дифференциальных уравнений параллельными блочными методами. Так, например, для наиболее употребительной формулы Адамса-Башфорта с m = 4 получим
W(4,4)
![]() .
.
Если на отрезке интегрирования взято сто узлов M = 100, то W(4,4)=5.62.
Литература
- Worland P.B. Parallel method for the numerical solution of ordinary differential equations.IEEE Trans.Comp.C-2,10 (1976) 1045-8.
- Дж. Холл,Дж. Уатт. Современные численные методы решения обыкновенных дифференциальных уравнений. М.: Мир,1979.-312с.
- Системы параллельной обработки. Под ред. Ивенса Д. – М.:Мир,1985. – 416с
- Молчанов И.Н. Введение в алгоритмы параллельных вычислений. АН УССР, Инст. Кибернетики им.В.М. Глушкова. Киев: Наукова думка. 1990,-128с
- Фельдман Л.П. Параллельные интерполяционные алгоритмы численного решения задачи Коши для обыкновенных дифференциальных уравнений на SIMD компьютере. Наук. пр. ДонДТУ. Серія: Проблеми моделювання i автоматизації проектування динамічних систем, випуск 10: – Донецьк:, 2000, с. 15-22.
- L.P. Feldmann Implementierung und Effizienzanalyse von parallelen blockartigen Simulationsalgorithmen für dynamische Systeme mit konzentrierten Parametern. In: Möller, D.P.F. (Hrsg.): Tagungsband 14. ASIM-Symposium Simulationstechnik in Hamburg, September 2000, SCS-Europe BVBA, Ghent/Belgium 2000, S. 241-246.
- L.P. Feldman, O.A. Dmitrieva, S. Gerber. Abbildung der blockartigen Algorithmen auf Parallelrechnerarchitekture. In: Tavangarian,D., Grützner,R. (Hrsg.): Tagungs-band 15. ASIM-Symposium Simulationstechnik in Rostock, September 2002, SCS-Europe BVBA, Ghent/Belgium 2002, S.359-364.