---

Авторы:

Л.П.Фельдман, e-mail: feldman@r5.dgtu.donetsk.ua

И.А. Назарова, e-mail: nazarova@r5.dgtu.donetsk.ua

Кафедра ПМиИ, ДонНТУ

83000, Донецк, ул. Артема, 58.

---

Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений

В статье предложен обзор работ авторов по параллельным методам решения задачи Коши для систем обыкновенных дифференциальных уравнений (СОДУ). Разработаны вычислительные схемы отображений методов на параллельные SIMD и MIMD архитектуры с различными топологиями соединения процессорных элементов: кольцо, решетка/тор, гиперкуб. Получены сравнительные характеристики потенциального и реального параллелизма, проведены численные эксперименты на системе тестов.

Parallel Algorithms for the Numerical Decision of Caushy’s  Problem for Ordinary Differential Equations systems

L.P. Feldman, I.A. Nazarova

Donetsk States Technical University

58, Artema str., Donetsk 830000, Ukraine

In this paper the review of parallel algorithms for the decision of ordinary differential equations systems is realized. The calculable schemes of methods reflection on parallel SIMD and MIMD computing structures with different topologies: ring, matrix/tore, hypercube are developed. The comparative descriptions of potential and real parallelism are got, the numerical experiments on the system of tests are conducted.

Введение

Моделирование реальных экономических, технических и других процессов, описываемых системами обыкновенных дифференциальных уравнений (СОДУ) большой размерности, представляет собой обширный класс задач, для решения которых применение высокопроизводительной вычислительной техники не только оправдано, но и необходимо. Об этом свидетельствует знаменитый список проблем “большой вызов”, в котором такие задачи занимают одно из ведущих мест. В данной статье приведен обзор работ авторов по конструированию параллельных алгоритмов численного решения нелинейной задачи Коши для СОДУ на основе явных и неявных одношаговых и многошаговых схем с альтернативными способами оценки апостериорной локальной погрешности, а также особенности применения этих методов для решения линейных задач. Предлагаемые алгоритмы ориентированы на использование в многопроцессорных вычислительных системах SIMD, MIMD и кластерной архитектуры с различными топологиями соединения процессорных элементов.

Численно решается задача Коши для системы обыкновенных дифференциальных в общем случае нелинейных уравнений (СОДУ) первого порядка размерности m с известными начальными условиями:

где         

1. Распараллеливание решения задачи Коши для СОДУ на основе явных и неявных одношаговых разностных схем

Современные теоретические исследования и вычислительные эксперименты в области параллельных вычислений показали, что наиболее эксплуатируемым способом создания параллельных методов является распараллеливание хорошо исследованных и многократно апробированных последовательных численных алгоритмов [1]. Развитым и общепризнанным математическим аппаратом разработки параллельных алгоритмов являются графовые модели: графы влияния, зависимостей и так далее, то есть некоторые информационные графы алгоритмов. Однако для реальных задач эта модель встречается с большими трудностями. Для прямого описания всех вершин и дуг соответствующего графа необходимы большие затраты компьютерной памяти, а для обработки или анализа используются графовые алгоритмы, большинство из которых имеет высокую вычислительную сложность, чаще всего экспоненциальную. Поэтому для разработки параллельных алгоритмов задач практического уровня сложности используется многоэтапный технологический процесс – иерархическая декомпозиционная методика. Первоначально вычислительная задача разбивается на подзадачи, анализируются информационные взаимосвязи между ними, определяется множество макроопераций, оценивается эффективность потенциального и реального параллелизма. В случае неудовлетворительного результата на любом из этапов схема разбиения изменяется, и весь процесс повторяется сначала до тех пор, пока характеристики полученного параллельного алгоритма не станут удовлетворительными или путем полного перебора не станет ясно, что добиться качественного распараллеливания невозможно. Графы влияния могут быть использованы для построения параллельного алгоритма, как на верхнем уровне для анализа взаимодействия подзадач, так и на нижнем уровне для распараллеливания отдельных макроопераций, соответствующих определенным подзадачам. Выбор декомпозиционной методики распараллеливания обусловлен преимуществами этого подхода, а именно: взаимозависимостью и итеративностью этапов построения параллельного алгоритма и возможностью обеспечить необходимый уровень масштабируемости вычислений за счет варьирования детальности декомпозиции.

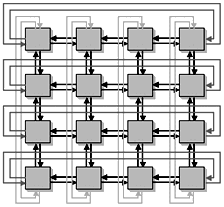
Для параллельных вычислений важным, а, иногда и определяющим, является учет сложности межпроцессорных связей. Поскольку параллельное решение задачи Коши использует структурное информационное взаимодействие по типу коммуникаций, предоставляется возможность разработать единые коммуникационные примитивы для различных операций передачи данных в различных топологиях. Наиболее используемые топологии: линейка/кольцо, решетка/ /тор, гиперкуб и две коммуникационные операции: передача данных между двумя процессорами сети – операция типа “point-point” и передача данных от всех процессоров сети всем процесcорам сети – множественная пересылка “all-to-all”.

Для оценки времени выполнения операции передачи одного сообщения объемом V байт между двумя процессами, локализованными на различных процессорах, при распределенной памяти использовалась следующая модель:

где t_s – латентность, длительность подготовки сообщения для передачи; l – длина маршрута; t_w– время передачи одного байта; y – число байт в слове; B – пропускная способность канала передачи данных (байт/секунда). Трудоемкость одиночной операции пересылки данных между двумя процесорами может быть получена путем подстановки длины диаметра сети в выражение (2). Для вычисления времени выполнения множественной пересылки в условиях той же модели необходимо определиться с выбором алгоритма маршрутизации. К числу наиболее распространенных оптимальных алгоритмов передачи данных относится класс методов покоординатной маршрутизации. Идея этих методов заключается в том, что поиск путей передачи данных осуществляется последовательно для каждой размерности рассматриваемой топологии. Сокращение времени передачи данных может быть достигнуто и за счет использования встречных обменов, когда данные передаются одновременно в обе стороны. Это позволяет добиться почти двойного уменьшения времени обмена данными по сравнению с однонаправленными обменами. Таким образом, в условиях существования двунаправленных линков имеем

– для кольцевой топологии:

Рис.1.  Топология кольцо или 1D – тор

1.1. Разработка и исследование эффективности параллельных алгоритмов решения задачи Коши для СОДУ на базе вных одношаговых схем типа Рунге-Кутты

Явные формулы Рунге-Кутты(ЯМРК) находятся среди старейших и хорошо изученных схем численного анализа. Однако, несмотря на наличие огромных и всесторонних знаний в этой области, ЯМРК продолжают быть источником активных исследований, особенно в таком новом научном направлении как параллельные вычисления. Потенциально явные методы Рунге-Кутты содержат два вида параллелизма:

- параллелизм метода (параллелизм во времени);

- параллелизм системы (параллелизм в пространстве).

Системный параллелизм реализуется через распределенные вычисления различных компонент системы, т.е. отдельных компонент шаговых коэффициентов и векторов решений. Параллелизм метода связан с выделением независимых субвычислений внутри одного шага метода и, как правило, значительно меньше системного. Для системы обыкновенных дифференциальных уравнений размерности m явный s-стадийный метод Рунге-Кутты имеет следующий вид:

Вычисление любой аппроксимации решения состоит в вычислении множества коэффициентов   и, собственно, приближенного решения Для явных схем вычисление шаговых коэффициентов есть сугубо последовательный последовательный процесс. Равенство нулю элементов a_ij  ,   матрице Батчера для ЯМРК определяет возможность одновременного вычисления определенных коэффициентов, однако дает очень незначительную степень параллелизма. Для разработки параллельного алгоритма использовался математический аппарат графов влияния [1].

Рис.4.       Граф влияния вычисления i-го шагового коэффициента

Задача распараллеливания в такой постановке сводится к отысканию максимального независимого множества вершин орграфа, причем вершинам графа сопоставляются выполняемые операции и вершины соединяются дугами тогда и только тогда, когда результат выполнения одной операции влияет на результат смежной. На рис.4 приведен граф влияния для вычисления вектора значений i-го шагового коэффициента в случае, если m=p.

В быть вычислены параллельно

1) l=m компонент при m=p;

2) l=ém/pù компонент при m>p.

После быть доступны всем процессорам. Реализация передачи данных осуществляется с использованием коммуникационной операции "all-to-all", затем каждый процессор вычисляет равную часть компонент вектора шаговых коэффициентов правой части исходной СОДУ. После распределенного вычисления всех шаговых коэффициентов параллельно вычисляется равное количество компонент вектора решений. Заметим, что дополнительных пересылок здесь не понадобится, так как каждый процессор на следующем временном шаге будет работать с той же частью компонент шаговых векторов и вектора решений.

Одним из главных вопросов, возникающих при численном решении систем обыкновенных дифференциальных уравнений, является проблема оценки погрешности приближенного решения. Априорная оценка глобальной погрешности разностного метода позволяет судить о сходимости приближенного решения задачи к точному и, следовательно, о его применимости. Апостериорная оценка локальной погрешности, получаемая на каждом шаге вычислений, позволяет автоматически выбирать шаг интегрирования, обеспечивающий заданную точность приближенного решения. Одношаговые методы, построенные способом Рунге-Кутты, в отличие от вычислительных правил, полученных на основе разложения решения в ряд по последовательным главным частям, непосредственно не представляют простой возможности судить о локальной точности найденного значения приближенного решения по результатам промежуточных вычислений. Параллельные алгоритмы решения задачи Коши, разработанные на основе явных численных схем, содержат встроенные альтернативные способы определения локальной апостериорной погрешности, а именно: дублирование шага по правилу Рунге; вложенные формы Рунге-Кутты (ВМРК); технология локальной экстраполяции.

Принцип удвоения шага является наиболее простым способом получения шаговой погрешности, однако он имеет большие накладные расходы: объем вычислений на один узел сетки возрастает почти втрое. Метод локальной экстраполяции является обобщением технологии удвоения шага по правилу Рунге. Идея метода заключается в многократном измельчении шага интегрирования, и также в многократном применении процесса локальной экстраполяции (см. рис.5). Решение задачи Коши рассматривается при переходе из точки x_n в точку x_n+1=x_n+H, H - базовая длина шага, H>0.

Рис.5. Схема вычисления i-й аппроксимации решения по технологии локальной экстраполяции

Выбирается ряд натуральных чисел такой, что n₁<n₂<…n_k-1<n_k<… и, соответственно, последовательность шагов h₁>h₂>…>h_k-1>h_k>…, где h_i=H/n_i. Задается опорный численный метод порядка r⁰ и, выполняя n_i шагов интегрирования Выполнив вычисления для ряда последовательных значений i, по рекуррентному соотношению определяют экстраполированные значения T_i,j+1 для произвольных i,j [2]. Этот процесс получил название локальная полиномиальная экстраполяция

                                                                                          (4)

Здесь величина b равна единице в общем случае, в то же время для симметричных опорных методов b равно двум. Достоинство этого метода состоит в том, что он дает полную таблицу результатов вычислений, которые образуют последовательность вложенных методов и позволяют оценить локальную погрешность, выбрать стратегию для методов переменного порядка. В табл.1 T_ij есть приближенное решение задачи Коши, полученное численным методом порядка r⁰+(j-1)b с шагом h_i.

Экстраполяционные методы имеют то преимущество, что у них на каждом шаге можно менять не только длину шага, но и порядок метода. Следовательно, экстраполяцию можно рассматривать как метод с переменным порядком (столбцы таблицы) и переменным шагом интегрирования (строки таблицы).

Для получения множества шагов интегрирования используются числовые последовательности, образованные гармоническим рядом, степенями двойки, различными четными рядами чисел

                                                                                                                
                                                                                                 (5)
                                                                                                         
                                                                                 

                                                                               

Вычислительная сложность формирования сеток интегрирования для произвольных опорных методов правой части системы исходных ОДУ

                                                      

где k – число строк экстраполяционной таблицы.

Необходимый размер экстраполяционной таблицы для получения решения методом порядка r, если исходный опорный метод имеет порядок r⁰, зависит от свойств опорного метода. При условии симметричности опорный метод имеет асимптотическое разложение по степеням h², и каждая экстраполяция исключает две степени h [2]. Для произвольного опорного метода каждая экстраполяция исключает одну степень h. Тогда количество строк экстраполяционной таблицы определяется одним из следующих соотношений:

– произвольный опорный метод:  r=r⁰+k-1;

– симметричный опорный метод: r=r⁰+2(k-1).

Таким образом, если вычислены k строк экстраполяционной таблицы, то для симметричных опорных методов имеем T_kk в качестве аппроксимации наивысшего порядка точности, равного 2k, для произвольных опорных методов соответственно – (k–1). Для управления шагом интегрирования естественно использовать выражение: ||T_k–1,k–T_k,k||. Определим накладные расходы на формирование последовательности сеток интегрирования, исходя из того, что при построении экстраполяционной таблицы для симметричных методов необходимо r/2 строк для достижения точности порядка r, а для произвольных методов – (r–1) строка. Например, если в качестве опорного метода выбирается явный метод Рунге-Кутты 2-го порядка точности, тогда оптимальной последовательностью для симметричных опорных методов является вторая четная последовательность с минимальным числом вычислений f, для которой N(r/2)=(r²+2r+4)/4. Для произвольных опорных методов наименее затратным является гармонический ряд. Теоретически нет никаких ограничений на длину экстраполяционной таблицы, однако ограниченность памяти машины и накапливание ошибок округления, ограничивают длину экстраполяционной таблицы сверху и, как правило, используется k_max≤10.

Таким образом, экстраполяционная технология включает: опорный численный метод решения задачи Коши, последовательность сеток, рекуррентное правило вычисления значений приближенного решения, и эффективность ее применения напрямую зависит от правильного выбора и сочетания всех трех составляющих. Заметим, что при разработке параллельных вычислительных схем для технологии локальной экстраполяции и дублирования шага появляется необходимость исследовать:

а) способы разбиения процессоров на группы, вычисляющие определенную аппроксимацию решения: равномерный, пропорциональный и комбинационный;

б) степень влияния порядка опорного метода на характеристики алгоритма в целом.

Одним из способов определения локальной апостериорной погрешности при решении задачи Коши являются вложенные методы Рунге-Кутты (ВМРК) или методы вложенных форм. Этот способ основан на использовании двух приближенных значений решения в одной точке, но в отличие от правила Рунге приближения вычисляются не по одной, а по двум формулам различных порядков одним и тем же шагом [2-3]. Для определения локальной погрешности как правило менее точного результата и управления величиной шага интегрирования используется величина d_n+1. К известным методам этого класса относят методы порядка (“оценщика погрешности”) получается как побочный продукт метода r-го порядка.

Общий вид вложенных методов на основе явных одношаговых s-стадийных методов Рунге-Кутты:

Анализ эффективности полученных параллельных алгоритмов производился на основе следующих показателей:

– времени решения при помощи последовательного алгоритма, T₁;

– времени решения при помощи параллельного алгоритма без учета - T_p,comp и с учетом обменных операций T_p=T_p,comp+T_p,comm, так называемые потенциальный и реальный параллелизм;

– коммуникационной сложности алгоритма в зависимости от выбранной топологии соединения процессоров и модели передачи данных;

– максимальной степени параллелизма, Dop;

– коэффициентов потенциального и реального ускорения, S=T₁/T_p и эффективности, E=S/p  параллельного алгоритма, а также масштабируемости на основе функции изоэффективности, f_E.

Динамические характеристики параллельных алгоритмов ЯМРК существенно зависят от многих факторов: размера задачи (m) и времени обращения к правой части исходной СОДУ (T_f), типа параллельного компьютера, размерноcти процессорных полей (p), времени выполнения арифметических операций (t_op), временных коммуникационных констант (латентность, t_s и время передачи одного слова, t_w), топологии межпроцессорного соединения. Определим, что при подсчете динамических характеристик алгоритмов: t_ad=t_mul=t_op – любая арифметическая опеРация с плавающей точкой выполняется за одно и то же время независимо от вида операции, это предположение справедливо для большинства современных компьютеров RISC архитектуры.

Под масштабируемостью будем понимать – возможность алгоритма обеспечить постоянное значение эффективности вычислений при увеличении числа процессоров (возможно за счет увеличения размерности задачи). Оценкой масштабируемости является функция изоэффективности [4], определяющая зависимость числа используемых процессоров для обеспечения постоянного уровня эффективности параллельных вычислений:

где W - показатель вычислительной сложности задачи (количество операций), K - коэффициент, зависящий только от значения показателя эффективности. Накладные расходы на параллелизм T₀=pT_p-W.

Построение функции изоэффективности – это попытка соединить в едином аналитическом выражении все перечисленные характеристики и оценить степень их влияния на качество параллельного алгоритма. Более того, это инструмент сравнения различных параллельных алгоритмов решения одной и той же задачи и определения условий, где использование одного алгоритма становится предпочтительнее, чем других.

Анализ теоретического выполнения параллельных методов решения нелинейной задачи Коши на базе ЯМРК и проведенный численный эксперимент позволяют сделать выводы:

– наиболее эффективными параллельными методами с точки зрения эффективности и ускорения являются вложенные методы;

– преимущества методов на базе локальной экстраполяции проявляются при получении высокоточных решений (10^-15-10^-20) и для СОДУ со сложными правыми частями.

Лучшие характеристики параллелизма, близкие к потенциальным, практически линейное ускорение и единичная эффективность для ЯМРК, достигаются при сочетании нескольких факторов: сложной правой части, причем T_f>>t_op, выполнении условия p£Dop, использовании топологии гиперкуб с синхронным или даже асинхронным выполнением обменов. Определение реальных характеристик параллелизма осуществлялось с помощью пакета MathematicaÒ(Wolfram Research Inc.), численный эксперимент проводился на базе тестов для СОДУ с использованием библиотеки MPI.

1.2. Разработка и исследование эффективности параллельных алгоритмов решения задачи Коши для СОДУ на базе ПНМРК

Исследование численных алгоритмов решения задачи Коши, основанных на конечно-разностных схемах, показало, что параллельные свойства таких алгоритмов во многом определяются видом лежащей в их основе численной схемы. Большим потенциальным параллелизмом обладают явные методы, однако присущие этим схемам недостатки, одним из которых является их условная устойчивость, ограничивает область применения таких алгоритмов. В этой связи значительный интерес представляют неявные схемы, которые несмотря на большую вычислительную сложность, не имеют альтернативы среди одношаговых методов при решении жестких задач.

Численное решение (1) полностью неявным s-стадийным методом типа Рунге-Кутта (ПНМРК) можно получить последовательно по шагам с помощью следующей схемы [2-3]:

                                                                (7)

где приближенное решение (1) на шаге n, s-размерные вектора c=(c₁,c₂,…,c_s), b=(b₁,b₂,…,b_s), и уникальный вариант метода и выбираются из соображений точности, h – выбранный шаг интегрирования. К достоинствам полностью неявных, одношаговых методов общего вида (на основе квадратурных формул Радо и Лобатто) следует отнести хорошие характеристики устойчивости и точности, достаточные для решения жестких задач. Так, например, s–стадийный метод РадоIA имеет порядок практически в 2 раза больше, чем число стадий и обладает A-устойчивостью. Недостатком этих методов является высокая вычислительная сложность, обусловленная итерационным процессом определения шаговых коэффициентов, которая не позволяет эффективно применять эти методы на последовательных машинах.

При решении систем ОДУ с использованием полностью неявных методов Рунге-Кутты все m×s неизвестных должны определяться одновременно, что существенно усложняет задачу (всего шаговых коэффициентов s и размерность каждого вектора равна m)

    

Для решения системы (7) используем следующий метод функциональной итерации:

                                                                            (8)

Здесь итерационный процесс, повторенный l раз l-ю аппроксимацию для Скорость сходимости итерационного процесса может быть определена следующим образом: r^*=min(r,N+1), где r - порядок используемого ПНМРК. Как и для всех уже рассмотренных методов , распараллеливание ПНМРК базируется на выполнении одного шага интегрирования. Все множество процессоров разбивается на s групп по числу шаговых векторов, затем передает их всем процессорам группы. Вычисление решения в следующей точке требует реализации операции множественная пересылка данных "all-to-all".

Межгрупповой обмен может быть осуществлен двумя способами:

1) каждый первый процессор в группе передает вектор первый элемент каждой другой группы + параллельный групповой обмен в каждой группе;

2) межгрупповая передача по типу “все-всем”.

Для неявных схем определение локальной погрешности с целью управления шагом интегрирования производилось на основе локальной экстраполяции Ричардсона и методов вложенных форм. Разработка и анализ эффективности полученных параллельных алгоритмов ПНМРК аналогичны как и для явных методов. Трудоемкость ВМРК и ПНМРК существенно зависит от правой части ОДУ (СОДУ). Для сложных правых частей ВМРК имеют меньшее время выполнения, чем неявные. Этот эффект увеличивается в том случае, если время арифметических операций больше времени обмена. В общем случае вложенные явные МРК имеют меньшую вычислительную сложность, чем неявные МРК и этот эффект увеличивается с увеличением порядка метода. Для вложенных методов трудоемкость коммуникационных операций зависит от числа этапов метода: s, для НМРК, и от числа итераций, причем с ростом порядка метода число этапов растет быстрее, чем число итераций.

Проведенные теоретические исследования и вычислительный эксперимент дают возможность говорить о том, что несмотря на большие накладные расходы, алгоритмы решения нелинейной задачи Коши для систем обыкновенных дифференциального уравнений на основе полностью неявных методов Рунге-Кутты при тщательном подборе всех параметров могут быть достаточно эффективно отображены на параллельные структуры с топологиями гиперкуб и тор при асинхронной передаче данных.

1.3. Особенности решения задачи Коши для линейных СОДУ на параллельных ВС

Экспоненциальный метод относится к специальным методам численного решения задачи Коши для систем линейных обыкновенных дифференциальных уравнений (СЛОДУ), основан на точном представлении решения в аналитической форме и вычислении матричной экспоненты. Предлагаемый метод особенно эффективен для решения систем с большой константой Липшица, в частности, для жестких систем уравнений [5]. Этот способ решения требует меньшего объема вычислений, чем стандартные методы и позволяет построить более простые и эффективные параллельные алгоритмы решения задачи Коши.

Общий вид задачи Коши для однородных СЛОДУ с постоянными коэффициентами:

                                                                             (9)

– вектор неизвестных; - вектор начальных условий; A – матрица коэффициентов линейной системы.

Приближенное решение (9) можно построить, аппроксимировав матричную экспоненту отрезком ряда Тейлора при малом h

                                                                              (10)

а затем, используя некоторый алгоритм умножения матриц, вычислить численное решение, причем, (10) определяет численный метод решения СЛОДУ с постоянными коэффициентами порядка r.

Решение задачи Коши для неоднородной системы:

имеет вид

             

Основной особенностью метода является возможность введения подготовительного этапа, который будет выполняться до начала интегрирования и вынести в него наиболее ресурсоемкие операции нахождения матричных форм, а именно матричное умножение, не зависящее от шага интегрирования. Матричная функция F(h) обладает следующим свойством: F(h)=F(h/2)F(h/2), что позволяет достаточно легко встраивать алгоритмы определения локальной погрешности на основе дублирования шага и локальной экстраполяции. Применение экспоненциального метода для вложенных форм делает практически ненужными вычисления по формуле высшего порядка

Для плотнозаполненных матриц имеется два принципиально различных класса последовательных алгоритмов умножения матриц: традиционные и рекурсивные методы быстрого умножения на базе алгоритмов Штрассена-Винограда [5]. В оригинале алгоритм Штрассена-Винограда – это алгоритм рекурсивного умножения блочных матриц половинного размера, где каждый блок квадратный, т.е. размерности матриц должны быть четными числами. Идея Штрассена может быть применена рекурсивно: если исходные матрицы A и B имели размеры n´n, то алгоритм быстрого умножения можно применять многократно (на самом нижнем уровне получим блоки 1´1). В классическом варианте, как известно, алгоритмы рекурсивного умножения матриц очень чувствительны к ошибкам округления, т.е. плохо обусловлены, что ограничило их область применения. В связи с этим предлагается использовать полиалгоритмы рекурсивного и блочного систолического умножения, что позволяет избежать указанных недостатков для умножения матриц практических размеров.

Для построения и исследования эффективности параллельных алгоритмов решения СЛОДУ на основе экспоненциального метода использовалась та же технология, что и для ЯМРК и НМРК общего вида. Проведенные исследования позволяют сделать выводы

- решение линейной задачи Коши на основе модифицированного экспоненциального метода с использованием локальной экстраполяции и вложенных форм имеет практически одинаковую вычислительную сложность, хотя локальная экстраполяция дает нам целую таблицу решений;

- наиболее эффективной топологией для реализации методов является решетка и ее замкнутый эквивалент тор, поскольку на такой топологической схеме наиболее эффективно выполняются матричные операции.

2. Параллельные блочные методы решения задачи Коши для СОДУ

В первой части статьи рассматривались вопросы построения параллельных алгоритмов решения задачи Коши посредством распараллеливания эффективных последовательных методов. С развитием параллельных ВС особое внимание уделяется теоретическим работам по построению новых параллельных алгоритмов решения поставленной задачи, однако практическое применение таких алгоритмов не всегда оправдано. Многие из них либо обладают численной неустойчивостью, либо имеют достаточно сложную структуру, приводящую к потере эффективности. К методам лишенным указанных недостатков, можно отнести параллельные блочные одношаговые и многошаговые k-точечные методы.

2.1. Параллельные вычислительные схемы блочных методов

В [6-9] подробно рассмотрены вопросы построения конкретных вычислительных схем блочных методов, приведено доказательство сходимости, дана оценка погрешности и алгоритм решения нелинейной разностной задачи, приведены тестовые примеры. Здесь введем обозначения, рассмотрим способы оценки локальной апостериорной погрешности для параллельных блочных методов и дадим оценку параллелизма.

Множество M точек равномерной сетки x_m,m=1,2,…,M и x_M=Hс шагом h разобьем на блоки, содержащие по k точек, kN³M. В каждом блоке введем номер точки i=0,1,…,k и обозначим через x_n,i точку n-го блока с номером i. Точку x_n,0 назовем началом блока n, а x_n,k – концом блока. Очевидно, имеет место x_n,k=x_n+1,0. Условимся начальную точку в блок не включать. При численном решении задачи Коши одношаговым блочным методом для каждого следующего блока новые k значений приближенного решения вычисляются одновременно с использованием  значения только в последней точке предшествующего блока.

Обозначим через y_n,i приближенное значение решения задачи Коши (1) в точке x_n,i обрабатываемого блока. Тогда для одношаговых блочных методов разностные уравнения имеют вид

                                                                    (11)

В случае многошагового блочного метода начальный блок будет содержать точки сетки, в которых заданы начальные значения приближенного решения, необходимые для продолжения расчета. В общем случае уравнения многошаговых разностных методов для блока из k точек при использовании вычисленных значений приближенного решения в m предшествующих блоку узлах, с учетом введенных выше обозначений можно записать в виде:

     n=1,2,… .                                              (12)

Определить коэффициенты a_i,j и b_i,j формул (11) и (12) можно интегро-интерполяционным методом, построив интерполяционный многочлен L_m+k-1(x) с узлами интерполяции x_n,j-m и соответствующими им значениями правой части уравнения (1)  

получим уравнения для выбранных m и k.

2.2. Методы с контролем  погрешности на шаге интегрирования

Для оценки локальной погрешности при решении одношаговым многоточечным методом используем идею вложенных форм. Решаются две задачи на одной сетке c одним и тем же шагом h:

первая – одношаговым k-точечным методом;

вторая – одношаговым (k+1)-точечным методом.

Второе решение необходимо для оценки локальной погрешности, поэтому основным является k-точечный метод. Используются значения приближенных решений в совпадающих k узлах основного блока. Лишняя k+1 точка является начальным приближением в расчетах решения в следующем блоке. Локальная погрешность приближенного решения одношаговым k-точечным методом в i-м узле блока определяется формулой

и для (k+1)-точечного метода локальная погрешность в том же узле определяется формулой

Вычитая из верхнего соотношения нижнее, получим представление главного члена погрешности k-точечного метода на шаге в виде

который может быть использован для оценки локальной погрешности.

Для оценки шаговой погрешности при решении многошаговым многоточечным методом используется аналогичный подход. Решаются две задачи на одной сетке c одним и тем же шагом h: первая – m-шаговым k-точечным методом; вторая – (m+1)-шаговым k-точечным методом. Второе решение используется для оценки локальной погрешности, поэтому основным является m-шаговый k-точечный метод. Оцениваются значения приближенных решений в совпадающих k узлах основного блока. Локальная погрешность приближенного решения m-шаговым k-точечным методом в i-м узле блока определяется формулой

а для (m+1)-шагового k-точечного метода локальная погрешность в том же узле определяется формулой:

Представление главного члена погрешности одношагового k-точечного метода на шаге

Таким образом, для главного члена погрешности получаем оценку:

Проведенный численный эксперимент полностью подтверждает полученные теоретические результаты.

2.3. Оценка эффективности параллельных блочных алгоритмов решения задачи Коши для СОДУ

При численном решении задачи Коши для сравнительной характеристики методов можно рассматривать различные показатели. В случае произвольной правой части уравнения о трудоемкости метода естественно судить по числу обращений для вычисления значений правой части уравнения на каждый узел сетки. Для оценки эффективности одношаговых блочных методов найдем отношение времени выполнения алгоритма Рунге-Кутты на однопроцессорной ЭВМ ко времени выполнения одношагового блочного алгоритма соответствующего порядка на параллельной ВС. Определим время выполнения алгоритма Рунге-Кутты (k+1)-го порядка точности на одном процессоре. Время последовательного вычисления приближенных значений решения с точностью O(h^k+1) во всех k узлах блока составит

T_s=(k+1)²t_f +k²(t_ad+t_mul).

Для параллельного выполнения вычислений по формулам (11) закрепим за каждым узлом блока процессор. При его реализации на k процессорах можно одновременно вычислять значения F_n,i,s, а затем также одновременно получить по формулам (11) значения y_n,i,s для каждого фиксированного s. Объединим процессоры в кольцо, чтобы иметь возможность одновременной передачи данных соседним процессорам. Обозначим через t_ta время передачи числа соседнему процессору. Время параллельного вычисления приближенных значений решения с той же точностью для всех узлов блока составит

Если учитывать только время вычислений правой части уравнения, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части, то ускорение k-точечного параллельного алгоритма можно считать приближенно равным

Для оценки ускорения m-шагового k-точечного блочного метода сравним время его выполнения на мультипроцессорной системе со временем выполнения алгоритмаm-шагового метода Адамса-Башфорта на однопроцессорной ЭВМ. Метод Адамса-Башфорта можно рассматривать как многошаговый одноточечный блочный метод. Последовательное k-кратное применение формул Адамса-Башфорта позволяет вычислить приближенное решение в тех же k узлах блока, в которых параллельно за k итераций может быть вычислено решение m-шаговым k-точечным блочным методом. В этом случае время вычисления будет приблизительно одинаково. Точность приближенного решения, полученного m-шаговым k-точечным блочным методом, имеет порядок O(h^m+k), а точность приближенного решения, полученного по m шаговой формуле Адамса-Башфорта, имеет порядок O(h^m+1). Поэтому для получения решения с одинаковой точностью для метода Адамса-Башфорта надо выбрать шаг сетки мельче в M^(k-1)/(m+k) раз, чем шаг для m-шагового k-точечного метода. Здесь M – число узлов сетки на отрезке решения задачи методом Адамса-Башфорта. Аналогично могут быть получены оценки эффективности решения задачи Коши для интегрирования СОДУ параллельными блочными методами.

Таким образом, в статье приведен обзор и анализ результатов исследований, посвященных параллельным методам численного решения задачи Коши для систем обыкновенных дифференциальных уравнений и является продолжением ранее опубликованных работ [6-15]. В обзор не вошли результаты исследований по распараллеливанию гибридных, многошаговых и многостадийных методов Рунге-Кутты, а также многошаговых методов типа Адамса-Башфорта и Адамса-Моултона.

Литература

1. Воеводин В.В., Воеводин Вл. В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002, 608с.
2. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990, 512 с.
3. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир, 1999, 685с.
4. Kumar V., Gupta A. Analyzing scalability of parallel algorithms and architectures // Journal of Parallel and Distributed Computing., 22(3), 1994, p.379-391.
5. Голуб Дж., Ван Лоун Ч. Матричные вычисления: Пер. с англ. – М.: Мир, 1999, 548с.
6. Фельдман Л.П. Параллельные алгоритмы моделирования динамических систем, описываемых обыкновенными дифференциальными уравнениями // Электронное моделирование, 2004, т.26, №1, с.19-30.
7. Feldman L.P., Dmitrieva O.A., Gerber S. Abbildung der blockartigen Algorithmen auf Parallelrechnerarchitekture. In: Tavangarian,D., Grützner,R. (Hrsg.): Tagungs-band 15. ASIM-Symposium Simulationstechnik in Rostock, September 2002, SCS-Europe BVBA, Ghent/Belgium 2002, s.359-364.
8. Feldman L.P. Implementierung und Effizienzanalyse von parallelen blockartigen Simulationsalgorithmen für dynamische Systeme mit konzentrierten Parametern. In: Möller, D.P.F. (Hrsg.): Tagungsband 14. ASIM-Symposium Simulationstechnik in Hamburg, September, 2000, SCS-Europe BVBA, Ghent/Belgium 2000, s.241-246.
9. Фельдман Л.П. Параллельные интерполяционные алгоритмы численного решения задачи Коши для обыкновенных дифференциальных уравнений на SIMD компьютере. Наук. пр. ДонДТУ. Серія: Проблеми моделювання i автоматизації проектування динамічних систем, випуск 10: – Донецьк:, 2000, с.15-22.
10. Фельдман Л.П., Назарова И.А. Применение технологии локальной экстраполяции для высокоточного решения задачи Коши на SIMD-структурах // Научные труды Донецкого национального технического университета. Выпуск 70. Серия: "Информатика, кибернетика и вычислительная техника" (ИКВТ-2003) – Донецк:ДонНТУ, 2003, с.98–107.
11. Назарова И.А., Фельдман Л.П. Масштабируемый параллельный алгоритм численного решения линейных СОДУ для компьютеров с распределенной памятью // Тезисы докладов V Международной конференции по неравновесным процессам в соплах и струях (NPNJ-2004), Самара, 5-10 июля 2004 г. – М.: Вузовская книга, 2004, с.153–155.
12. Назарова И.А., Фельдман Л.П. Эффективность параллельного численного решения нежестких систем обыкновенных дифференциальных уравнений с контролем локальной погрешности // Тезисы докладов XX Международного семинара по струйным, отрывным и нестационарным течениям. Санкт-Петербург. 1-3 июля 2004г. – СПб.: ИПЦ СПбГУТД, 2004, с.201–202.
13. Назарова И.А. Эффективность численного решения нежестких СОДУ с контролем локальной погрешности для компьютеров с распределенной памятью // Искусственный интеллект 3’2004. – Донецк, 2004, с.212-216.
14. Назарова И.А. Параллельные полностью неявные методы численного решения жестких задач для СОДУ // Искусственный интеллект 3’2005. – Донецк, 2005, с.185-193.
15. Назарова И.А., Фельдман Л.П. Разработка и анализ эффективности параллельных алгоритмов итерационных методов численного решения СОДУ для мультипроцессоров с распределенной памятью. Тезисы докладов XIV Международной конференции по вычислительной механике и современным прикладным программным средствам. –  М.: Вузовская наука, 2005, с.343-345.