АНАЛИЗ ПАРАЛЛЕЛЬНЫХ АЛГОРИТМОВ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕТОДАМИ АДАМСА-БАШФОРТА И АДАМСА-МОУЛТОНА

Автор: Дмитриева O.А.
Донецкий национальный технический университет
83000, Донецк, ул. Артема, 58
e-mail: dmitriv@r5.donntu.ru
http://www.imamod.ru/magazin/pdf/12/1205-081r.pdf

Введение

В течение последних двух-трех десятилетий пиковая производительность параллельных вычислительных систем возросла на несколько порядков. Радикально изменились технологическая база и архитектура. Но главным препятствием к внедрению практически всех параллельных архитектур является отсутствие параллельных алгоритмов. Речь, в первую очередь, идет о больших системах дифференциальных уравнений, как обыкновенных, так и в частных производных, являющихся основой больших современных научных и инженерных задач. Многие численные методы решения приходится пересматривать, а от некоторых полностью отказываться. В то же время, целый ряд вопросов, которые были несущественны или вообще не возникали при проведении последовательных вычислений, приобрели исключительную важность для эффективного и правильного использования вычислительных систем. Опыт эксплуатации параллельных систем показал [1]. что для эффективного их применения нужно радикально менять структуру численных методов. Эти обстоятельства послужили основой для адаптации известных методов решения систем обыкновенных дифференциальных уравнений (ОДУ) на параллельных системах с SIMD архитектурой.

Численное решение систем ОДУ методами Адамса-Башфорта и Адамса-Моултона на решетке процессоров

Численное решение задачи Коши для системы обыкновенных дифференциальных урав¬нений с постоянными коэффициентами

где

можно получить последовательно по шагам с помощью, например, следующих формул Адамса-Башфорта и Адамса-Моултона [2]

где h - выбранный шаг интегрирования.

Приведенный метод в целом является явным. Сначала по формуле Адамса-Башфорта вычисляется значение х_k+1^(р) являющееся прогнозом для х_k+1. Затем х_k+1^(р) используется для расчета скорректированного значения х_k+1^(k), вычисляемого по формуле Адамса-Моултона. Представляемый метод имеет четвертый порядок точности, хотя можно получить эти методы сколь угодно высокого порядка, используя все большее число предыдущих точек, а, следовательно, интерполяционный полином более высокой степени. При этом с ростом точности формулы становятся все более громоздкими, но принцип остается тем же. Многошаговые методы порождают проблему, которая не возникала при использовании одношаговых методов, поскольку для начала счета им необходимо несколько разгоночных значений. При этом, однако, существенно, чтобы эти стартовые значения были вычислены с той же степенью точности, с которой будет работать многошаговый метод. Для этой цели предполагается использование метода Рунге-Кутты четвертого порядка точности, подробное описание реализации ко¬торого на параллельных архитектурах типа SIMD представлено в [3].

Модель, на которую ориентируется решение, имеет следующие особенности: используется вычислительная система SIMD структуры с квадратной сеткой, содержащей m*m процессорных элементов (ПЭ); каждый процессорный элемент может выполнить любую арифме¬тическую операцию за один такт; временные затраты, связанные с обращением к запоминаю¬щему устройству, отсутствуют. Для простоты изложения рассматривается случай, когда количество процессорных элементов в каждой строке совпадает с размерностью задачи. Для эффективной работы методов Адаме а в каждый процессорный элемент, имеющий индексы i,j, пересыпается элемент исходной матрицы матрицы А, приведенной предварительно к виду (3).

Таким преобразованием можно избавиться от сдвигов, необходимых на каждом шаге для подготовки систолического умножения матрицы на вектор. Подробно систолический алгоритм умножения рассмотрен в [3].

Из вектора неизвестных х формируется новая матрица U (см. (5)), элементы которой также пересылаются в соответствующие процессорные элементы. Таким образом, в каждом процессорном элементе с индексами i,j оказывается соответствующее значение g_i,j и элемент матрицы u_i,j. Первоначально выполняется умножение g_i,j*U_i,j во всех процессорных элементах. Затем осуществляется одиночный циклический сдвиг полученных значений и сложение содержимого процессорных элементов. Количество позиций, на которое производится очередной сдвиг, определяется элементами следующего ряда: 2⁰,2¹,2²,...,2^k-1, где k - ближайшее целое сверху [log₂m]. Учитывая, что в процессорных элементах уже находятся рассчитанные ранее значения для предыдущих точек, произведем необходимые операции умножения и сложения.

Легко видеть, что на такой сетке в каждом ПЭ i-й строки получается новое значение x_i^(p) на (n+1)-м шаге. Вычисление всех значений x_n+1^(p) определяется временем, затрачиваемым на одно умножение t_умн, суммой времен, необходимых для осуществления сдвигов и сложения сдваиванием , а также временами 4t_умн - умножение хранящихся значений на новые коэффициенты, 3t_сл - суммирование полученных результатов, 4t_умн+3t_сл - время для умножения на h/24 и суммирования со значением, полученным на предыдущем шаге. Всего получаем

Но необходимо учесть, что это время характеризует только нахождение значений век¬тора неизвестных прогнозируемых значений. При этом, получающиеся в сетке процессорных элементов значения расположены не в том порядке, как при изначальной засылке (5), а имен¬но в виде (6)

Для того, чтобы выполнить расчет скорректированных значений, нужно потратить какое-то время на переупорядочивание элементов, для приведения их к виду (5). На это потребуется m-1 циклических сдвигов по столбцам (в первом - 0, во втором - 1, .... в m столбце необходимо выполнить 2^k-1 сдвигов). Итого дополнительно потребуется времени (m-1)*t_сдв. После этого для получения скорректированных значений нужно повторить ту же последовательность операций, но с другими значениями. Общее время, затрачиваемое на нахождение вектора неизвестных х_n+1 на решетке процессоров m*m, оценивается как

Для оценок качества рассмотренного алгоритма используются наиболее распространенные критерии [4]: коэффициент ускорения и коэффициент эффективности , где T_i(N) - время вычисления вектора x_n+1 на однопроцессорной ЭВМ с быстродействием арифметического процессора и объемом ОЗУ, равным суммарному объему всех ЗУ арифметических процессоров, и с необходимым числом внешних устройств, имеющих скорости обмена такие же, как в многопроцессорной вычислительной системе типа SIMD. При расчете значений вектора x_n+1 на однопроцессорной ЭВМ потребуется время, равное

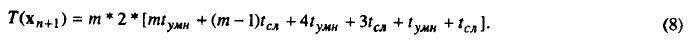
Чтобы оценить параллелизм алгоритма, можно принять [4], что t_оп=t_умн=t_сл=10t_сдв. Тогда

Эффективность методов Адамса при решении на SIMD структуре

Полученные результаты значительно отличаются от характеристик потенциального параллелизма методов Адамса (ускорение ускорение примерно равно m², эффективность - 1), поскольку при расчете этих характеристик не учитывались времена, затрачиваемые на сдвиги, хотя, как оказалось, эти времена существенно влияют на характеристики параллелизма (рис.1).

Реализация методов Адамса на линейке процессоров

Еще одним часто встречающимся способом коммутации параллельных вычислительных систем является линейка процессоров. Рассмотрим решение задачи (1) на модели SIMD-структуры, построенной из последовательно соединенных процессорных элементов (последний связан с первым) при условиях, оговоренных выше. Из всех рассмотренных способов первоначальной засылки значений в процессорные элементы оптимальным оказался способ, когда в 1-й процессорный элемент записываются значения i-й строки матрицы А: a_i1,a_i2,...,a_im и значения векторов неизвестных, полученных на предыдущих шагах, первоначально: x₍₀₎, x₍₁₎, x₍₂₎, x₍₃₎ , а на (n+1)-м шаге x_(n), x_(n-1), x_(n-2), x_(n-3). При таком подходе одновременно все процессоры могут начать проводить вычисления прогнозируемых значений по формулам (2). Через время m*t_умн+(m-1)t_сл+4t_умн+3t_сл+t_умн+t_сл=2m*t_оп+8t_оп в каждом i-м процессорном элементе получаем прогнозируемое значение x_n+1(i)^(p). Эти действия необходимо выполнить только один раз, перед началом основных вычислений и хранить в каждом i-м процессорном элементе получившиеся значения:

Теперь необходимо передать полученные прогнозируемые значения по типу «все-всем», так как в каждом процессорном элементе нам необходимо иметь значения векторов x_n+1^(p). Время, затрачиваемое на обмены, определится, как (m-1)t_сдв, после чего в каждом ПЭ будут содержаться векторы прогнозируемых значений в виде (11) и потребуется еще время на переупорядочивание элементов и приведение их к виду (12). При этом значения, хранящиеся в первом ПЭ останутся без изменений, во втором на их переупорядочивание потребуется время (m-1)t_сдв, в третьем (m-2)t_сдв в последнем t_сдв. Учитывая, что все сдвиги могут выполняться одновременно, нужное расположение значений получается за время (m-1)t_сдв, тогда общее время, затрачиваемое на распространение «все-всем» осуществится за время 2(m-1)t_сдв.

Вторая группа сдвигов, потребовавшаяся на переупорядочивание значений, может быть исключена, если провести первоначальную перестановку элементов в строках, т.е. записать в каждый (i-Й процессорный элемент i-ю строку матрицы G(3). Тогда после получения в каждом ПЭ прогнозируемого значения, передача «все-всем» может быть осуществлена за время (m-1)t_сдв. Перед расчетом скорректированного значения х_n+1^(k) из ПЭ удаляются значения х_n-3 как уже не использующиеся. Для расчета скорректированного значения потребуется время m*t_умн+(m-1)t_сл+4t_умн+3t_сл+t_умн+t_сл=2m*t_оп+8t_оп , рассылка «все-всем» (m-1)t_сдв Приняв t_сдв=0,1*t_оп, можно сказать, что полный цикл расчета значений для одной точки закончится через

Ускорение определим как

И, хотя ускорение получилось меньше, чем на решетке процессоров, но, учитывая, что эффективность работы этого алгоритма , можно говорить, что решение системы обыкновенных дифференциальных уравнений методами Адаме а предпочтительнее проводить на линейке процессоров. Сравнительные оценки качества рассмотренных алгоритмов параллельного решения систем обыкновенных дифференциальных уравнений по критериям ускорения и эффективности приведены на рис. 1.

Заключение

В представленной работе сделана попытка адаптации существующих алгоритмов решения систем обыкновенных дифференциальных уравнений большой размерности к архитектурам многопроцессорных вычислительных структур типа SIMD. Предложены параллельные варианты реализации методов Адамеа-Башфорта и Адамса-Моултова на решетке и на линейке процессоров. Оценки эффективности использованных методов, реализованных на линейке, значительно превосходят те же показатели на решетчатых структурах, что, с одной стороны не согласовывается с теоретическими оценками, а, с другой стороны, еще раз доказывает, что в параллельных вычислительных структурах время обменов данными может составлять большую часть общего времени решения задачи. Поэтому подходить к выбору структуры вычислительной системы для решения каждой конкретной задачи необходимо не только с позиций наращивания количества процессорных элементов, но и оптимизации алгоритмов для сокращения количества обменов между ними.

1. Воеводин В.В. Информационная структура алгоритмов. -М.: Изд-во МГУ, 1997, 139с.

2. Ортега Дж„ Пул У. Введение в численные методы решения дифференциальных уравнений / Пер. с англ.; Под ред. Абрамова А.А.-М.: Наука, Гл. ред. физ.-мат. лит., 1986, 288 с.

3. Фельдман Л.П. Параллельные алгоритмы моделирования динамических систем, описываемых обык¬ новенными дифференциальными уравнениями. Научн. тр. ДонГТУ, Вып. 6, Донецк: ДонГТУ, 1999, 330с.

4. Ортега Дж. Введение в параллельные и векторные методы решения линейных систем: Пер. с англ. - М.: Мир, 1991, 367с.