Автореферат:
Вступление
Колебательное движение частиц упругой среды, распространяющееся в виде волн – можно представить в виде спектра последовательных значений громкости для тонов различной высоты.
Подобные преобразования можно выполнять с помощью математических методов практически над любыми колебательными процессами — от световых волн и океанских приливов до циклов солнечной активности. Пользуясь этими математическими приёмами, можно раскладывать функции, представляя колебательные процессы в виде набора синусоидальных составляющих — волнообразных кривых, переходящих от максимума к минимуму, затем опять к максимуму, подобно океанской волне. Преобразование Фурье — это функция, описывающая амплитуду и фазу каждой синусоиды, соответствующей определённой частоте. Амплитуда представляет высоту кривой, а фаза — начальную точку синусоиды. Ниже на рисунке представлен пример преобразования Фурье для солнечного света, который, проходя это преобразование, разделяется на спектр (синусоидальные сигналы различной амплитуды и частоты):
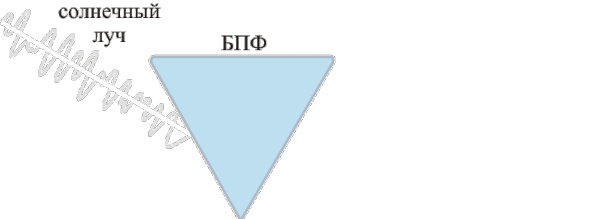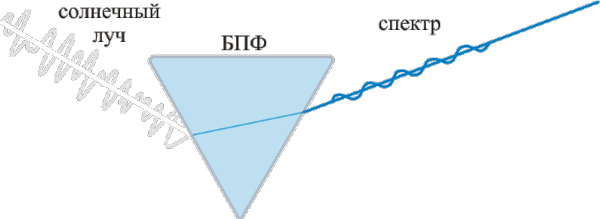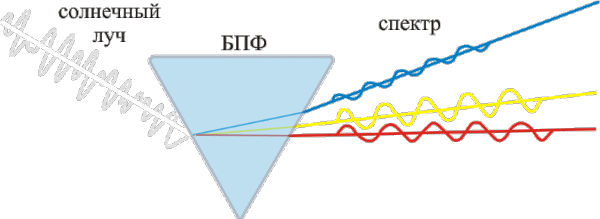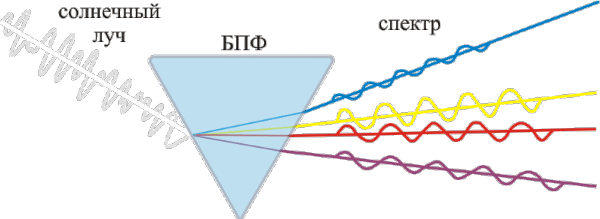
Рисунок 1 – Разложение солнечного луча на составляющие с помощью БПФ (анимация: объем - 24,2 КБ; размер - 600x219; количество кадров - 5; задержка между кадрами - 1с; задержка между последним и первым кадрами - 2 с; количество циклов повторения - 7.)
Первым человеком, поведавшим миру об этом методе, был французский математик Жан Батист Жозеф Фурье, именем которого и было названо преобразование. В то время он занимался изучением механизма теплопроводимости в металлах. Анализ Фурье был вызовом математическим теориям, которых твёрдо придерживались его современники. В начале XIX века многие выдающиеся парижские математики, в том числе, такие как Лагранж, Лаплас, Лежандр, Био и Пуассон, не могли принять утверждение Фурье о том, что любое исходное распределение температуры можно разложить на составляющие в виде главной гармоники и гармоник более высоких частот. Леонард Эйлер также считал идеи Фурье ошибочными, хотя к тому времени сам пришёл к выводу, что некоторые функции можно представить суммой синусоид. И когда Фурье огласил своё утверждение на одном из заседаний Французской академии наук, Лагранж заявил, что это невозможно. Тем не менее, несмотря на все эти сомнения, многие исследователи, в том числе математик Софи Жермен и инженер Клод Навье, начали расширять сферу исследований Фурье, выведя их за пределы анализа теплопроводности. А математиков тем временем продолжал мучить вопрос о том, может ли сумма синусоидальных функций сходиться к точному представлению разрывной функции.[7]
Математические основы преобразования Фурье
Развивавшаяся на протяжении почти двух столетий теория, связанная с преобразованием Фурье, теперь уже окончательно сформировалась. При помощи анализа Фурье пространственная или временная функция разбивается на синусоидальные составляющие, каждая из которых имеет свою частоту, амплитуду и фазу. Преобразование Фурье — это функция, представляющая амплитуду и фазу, соответствующие каждой частоте. Преобразование можно получить двумя различными математическими методами, один из которых применяется, когда исходная функция непрерывна, а другой — когда она состоит из множества отдельных дискретных измерений.
Независимо от способа, которым получается преобразование, для каждой частоты необходимо указать два числа. Это могут быть амплитуда и частота, однако ту же информацию могут кодировать и другие пары чисел. Эти значения можно выразить в виде одного комплексного числа. (Комплексное число представляет собой сумму одного действительного числа с другим действительным числом, умноженным на квадратный корень из минус единицы.) Таким представлением пользуются очень широко, так как оно позволяет привлечь математический аппарат алгебры комплексных чисел. Теория функций комплексных переменных и преобразование Фурье стали необходимыми в численных вычислениях, проводимых при конструировании электрических цепей, анализе механических колебаний и изучении механизма распространения волн.
Последовательность N комплексных чисел x0, …, xN-1 преобразуется в последовательность из N комплексных чисел X0, …, XN-1 с помощью дискретного преобразования Фурье по формуле [6]:
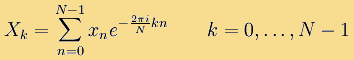
где i — это мнимая единица. Обратное дискретное преобразование Фурье задается формулой
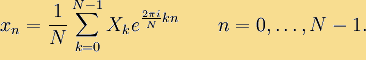
Актуальность проблемы и сферы применения
Количество необходимых арифметических операций зависело от числа точек, требовавшегося для описания волновой функции. Количество сложений было примерно таким же, что и число точек, а количество умножений было равно квадрату числа точек. Например, для анализа волновой функции, заданной 1000 точек, равномерно распределённых на интервале, необходимо было выполнить примерно 1000 сложений и ровно один миллион умножений.
Расчёты подобного рода стали более доступными с появлением компьютеров и специальных программ, реализующих новые методы анализа Фурье. Один такой метод был разработан в 1965 году Джеймсом У. Кули из Исследовательского центра им. Томаса Уотсона корпорации IBM и Джоном У. Тьюки из Bell Telephone Laboratories в Муррей-Хилле (шт. Нью-Йорк). Их работа привела к созданию программы, получившей известность как быстрое преобразование Фурье.
В быстром преобразовании Фурье время вычислений экономится за счёт уменьшения количества умножений, необходимых для анализа кривой. В то время количество умножений имело такое важное значение просто потому, что операция умножения выполнялась значительно медленнее других машинных операций, таких как сложение, считывание из памяти или записать данных в память.
В методе быстрого преобразования Фурье кривая делится на большое число равномерно распределённых выборочных значений. Количество умножений, необходимое для анализа кривой, уменьшается наполовину при таком же уменьшении количества точек. Например, кривая с 16 выборочными значениями обычно требует 16 в квадрате, или 256 умножений. Но предположим, что кривая была поделена на два интервала, по 8 точек в каждом. В этом случае количество умножений, требующихся для анализа каждого интервала, равно 82, или 64. В сумме для обоих интервалов получаем 128, или половину от исходного количества.
Но если при делении последовательности точек пополам мы получаем двукратную выгоду, то почему бы не продолжить эту стратегию дальше? Продолжив процесс разбиения, мы придём к восьми неделимым сегментам, по две точки в каждом. Преобразование Фурье для этих двухточечных сегментов можно вычислить, не прибегая к операции умножения, однако операции умножения всё же потребуются при комбинировании двухточечных преобразований в единое целое. Сначала 8 двухточечных преобразований объединяются в 4 четырёхточечных, а затем — в 2 восьмиточечных, и наконец последние сливаются в одно искомое 16-точечное преобразование. На каждой из этих трёх стадий объединения сегментов требуется по 16 операций умножения, и таким образом, полное количество умножений будет равно 48, что составит лишь 3/16 от исходных 256.
Часто это преобразование применяются и в биологии. Так, например, форма двойной спирали ДНК была открыта в 1962 году с использованием дифракции рентгеновских лучей в сочетании с анализом Фурье. Рентгеновские лучи фокусировались на кристалле волокон ДНК, и изображение, получаемое при дифракции излучения на молекулах ДНК, фиксировалось на пленке. Эта дифракционная картина давала информацию об амплитуде при применении преобразования Фурье к кристаллической структуре. Информация о фазе, которую невозможно было извлечь из одних только фотографий, выводилась путём сопоставления дифракционной картины ДНК с картинами, полученными при анализе сходных химических структур. По интенсивности рентгеновских лучей и фазовой информации, полученной из преобразования Фурье, биологи смогли восстановить кристаллическую структуру, т.е. исходную функцию. В последние годы изучения дифракции рентгеновских лучей в сочетании с подобным «обратным» анализом Фурье позволили определить структуру и многих других органических молекул, а также более сложных образований, в частности вирусов.
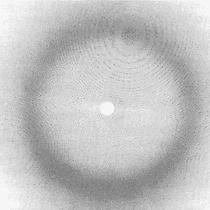
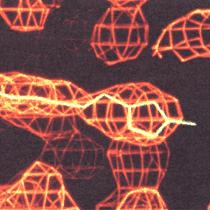
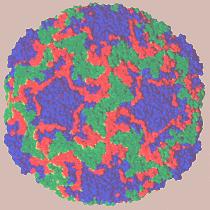
Рисунок 2 - построение модели вируса на основе информации полученной с помощью обратного преобразования Фурье над снимком взаимодействия рентгеновских лучей с электронами вируса.
Анализ Фурье позволяет трансформировать наблюдаемую картину дифракции рентгеновских лучей в молекулярные модели. Например, при взаимодействии рентгеновских лучей с электронами молекул вируса на фотоплёнке образуются своеобразные картинки (слева). Они представляют собой часть преобразования Фурье, применённого к молекулярной структуре вируса. Если обратить процесс преобразования, можно установить исходное распределение электронов, а стало быть, и атомов (в центре). По этим распределениям строится модель вируса (справа). Различными цветами здесь выделены различные белки [1].
С помощью анализа Фурье специалисты из Национального управления по аэронавтике и исследованию космического пространства повышают чёткость изображений небесных тел, сфотографированных с космических аппаратов. Автоматические межпланетные станции и искусственные спутники Земли передают информацию на Землю в виде последовательностей радиоимпульсов. Компьютеры обрабатывают эти импульсы с помощью методов Фурье. При этом компьютер модулирует отдельные компоненты каждого преобразования, чтобы чётче выделить одни свойства и устранить другие, аналогично тому, как с помощью преобразования Фурье устраняется шум из сигнала музыкальной записи. В конечном итоге изменённые таким образом данные опять преобразуются к исходной форме, и тем самым восстанавливается изображение. При помощи описанного процесса можно резче сфокусировать изображение, отфильтровать туманный фон и отрегулировать контрастность.
Существуют три основные области применения таких преобразований для обработки изображений. Во-первых, преобразования используются для выделения характерных признаков изображения. Так, например, постоянная составляющая спектра Фурье пропорциональна средней яркости изображения, а высокочастотные составляющие характеризуют величину и ориентацию его контуров. Другой областью применения преобразований является кодирование изображений, когда ширина спектра уменьшается за счет отбрасывания или грубого квантования малых по величине коэффициентов преобразования. Третья область – это сокращение размерности при выполнении вычислений. Иначе говоря, в процессе обработки (например, фильтрации) малые коэффициенты преобразования можно отбросить без заметного ухудшения качества обработки.
Процедура фильтрации изображения, основанная на преобразовании Фурье, содержит следующие шаги[2]:
- прямое преобразование Фурье;
- анализ спектра сигнала по Фурье образу и выбор типа фильтра и его параметров;
- генерация фильтра и его применение к Фурье образу;
- обратное преобразование Фурье для получения отфильтрованного изображения.
Преимуществом Фурье фильтрации является возможность в реальном масштабе времени анализировать спектр сигнала, на базе этого анализа гибко подбирать параметры фильтра и наблюдать результат фильтрации с последующей коррекцией параметров фильтра, если в этом есть необходимость.
В процессе выполнения данной работы планируется получить результаты по эффективности параллельной реализации БПФ для цифровых изображений. Будут рассчитаны временные затраты и затраты вычислительных ресурсов. Также планируется выделить классы изображений, для которых будут максимально эффективными те или иные преобразования.
Наиболее эффективно преобразование Фурье размерностью, являющейся степенью двойки. В реальных задачах часто размерность ДПФ таковой не является. Тогда задачу сводят к таковой, но это не всегда удобно. Существуют алгоритмы, позволяющие решать эту задачу, не прибегая к ее увеличению[3].
- алгоритм Кули - Тьюки быстрого преобразования Фурье;
- алгоритм Кули - Тьюки по основанию два;
- алгоритм Гуда - Томаса быстрого преобразования Фурье;
- алгоритм Герцеля;
- вычисление преобразования Фурье с помощью свертки;
- алгоритм Винограда для быстрого преобразования Фурье малой длины.
Планируемые результаты и научная новизна работы
В результате планируется применять к изображениям именно те алгоритмы, которые будут максимально эффективны для данного класса изображений.
Руководителем были поставлены такие задачи:
- Анализ существующих алгоритмов БПФ для цифровых изображений;
- Программирование реализации алгоритмов БПФ;
- Разработка параллельной реализации алгоритмов БПФ, с анализом существующих реализаций, на примере реализации с помощью бесплатной библиотеки MPI. [5];
- Оценка временных затрат при выполнении параллельных и последовательных алгоритмов БПФ.
Выводы
Благодаря широкому применению метода Фурье и сходных с ним аналитических методов мы и сегодня можем повторить с полным основанием то, что лорд Кельвин сказал в 1867 году: «Теорема Фурье не только является одним из самых изящных результатов современного анализа, но и даёт нам незаменимый инструмент в исследовании самых трудных вопросов современной физики».
И благодаря универсальности подхода, у данного метода широчайший спектр применения, в том числе и для обработки цифровых изображений.
В дальнейшем при выполнении магистерской работы будет разработана программная система для выполнения быстрого преобразования Фурье параллельным блочным методом. И на основании данных, полученных с помощью этой системы, представится возможным оценить показатели эффективности параллельного решения БПФ для изображений различного вида.
Список используемой литературы
1. Ronald N. Bracewell. The Fourier Transform and its Applications (second edition, revised). McGraw-Hill Book Company, 1986.
2. Прэтт У. Цифровая обработка изображений: Пер. с англ.—М.: Мир, 1982.— Кн.1—312 с.
3. Гонсалес Р. Вудс Р. Цифровая обработка изображений Москва: Техносфера, 2005. – 1072 с.
4. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов Москва «Мир» 1989.—448 с.
5. www.fftw.org Официальный сайт сообщества специалистов, занимающихся проблемой параллельной реализации алгоритмов БПФ.
6. www.wikipedia.org Описание дискретного преобразования Фурье в свободной энциклопедии "Википедия".
7. Рональда Н. Брейсуэлл. Журнал Scientific American (Издание на русском языке) № 8 · АВГУСТ 1989 · С. 48–56.
8. Воеводин В.В.,"Вычислительная математика и структура алгоритмов.".-М.: Изд-во МГУ, 2006.-112 с.
9. Говидараю Н.К., Ллойд Б., Доценко Ю., Смит Б., Манферделли Д. Высокопроизводительные дискретные преобразования Фурье на графических процессорах
10. Потопальский В.В. Оценка качества преобразования Фурье в радиотехнических и телевизионных системах. Львов, 1993. 189 с.
11. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. Москва, Мир – 1989. —448 с.
