Супонин Олег Олегович

Факультет Компьютерных Наук и Технологий

Кафедра Компьютерной Инженерии

Системное программирование

Группа СП-12м

Разработка моделей параллельной системы
прогнозирования поведения движущегося объекта

Научный руководитель: д.т.н, проф. Святный В.А

Консультант: Кривошеев С.В.

Резюме Биография

Реферат

Библиотека Ссылки Отчет о поиске Индивидуальный раздел

Содержание

Введение

1 Актуальность темы

2 Алгоритм генерации траектории

2.1 Алгоритм Флойда-Уоршелла

2.2 Алгоритм Дейкcтры

3 Фильтр Калмана

3.1 Модель динамической системы

4 Параллельные архитектуры

4.1 Параллелизм как основа высокопроизводительных вычислений

4.2 Параллельные архитектуры GPU

5 Подходы и реализации

Введение

Технический прогресс сделал значительный шаг вперед и сегодня существует огромное множество проектов, основной задачей которых является отслеживания подвижных объектов в пространстве, выполнение всевозможных операции контроля и управления над ними. В связи с этим для всех подобных объектов необходимо рассчитывать и прогнозировать траекторию и характеристику их движения.

1 Актуальность темы

Прогнозирование поведения движущегося объекта в настоящее время является актуальным вопросом, который заключается в том, что необходимо заранее знать возможные пути поведения объекта в зависимости от внешних факторов и заданных критериев. Необходимо решать проблемы временного ограничения, связанные с расчетом и определением местоположения объекта.

2 Алгоритм генерации траектории

Расчет траектории осуществляется с помощью различных алгоритмов, основными из которых являются: алгоритм Флойда-Уоршелла и Дейкстры.

2.1 Алгоритм Флойда-Уоршелла

Данный алгоритм предназначен для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом. Более строгая формулировка этой задачи следующая: [4]
есть ориентированный граф G = (V, Е) каждой дуге v -> w этого графа сопоставлена неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин v, w) любого пути от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.

Формальное описание
Имеются последовательно пронумерованные от 1 до n вершины графа. Алгоритм Флойда использует матрицу А размера п * n, в которой вычисляются длины кратчайших путей. Вначале A[i, j] = C[i, j] для всех i != j. Если дуга i -» j отсутствует, то C[i, j] = infinity. Каждый диагональный элемент матрицы А равен 0.

Над матрицей А выполняется п итераций. После k-й итерации A[i, j] содержит значение наименьшей длины путей из вершины i в вершину у, которые не проходят через вершины с номером, большим k. Другими словами, между концевыми вершинами пути i и у могут находиться только вершины, номера которых меньше или равны k. На k-й итерации для вычисления матрицы А применяется следующая формула:
A_k[i,j]=min(A_k-1[i,j], A_k-1[i,k]+A_k-1[k,j])
Нижний индекс k обозначает значение матрицы А после k-й итерации, но это не означает, что существует п различных матриц, этот индекс используется для сокращения записи. Для вычисления A_k[i, j] проводится сравнение величины A_k-i[i, j] (т.е. стоимость пути от вершины i к вершине j без участия вершины k или другой вершины с более высоким номером) с величиной A_k-1[i, k] + A_k-1[k, j] (стоимость пути от вершины i до вершины k плюс стоимость пути от вершины k до вершины j). Если путь через вершину k дешевле, чем A_k-1[i, j], то величина A_k[i, j] изменяется.

Оценка сложности
Время выполнения этой программы имеет порядок 0(V³), поскольку в ней только три вложенных друг в друга цикла. Доказательство «правильности» работы этого алгоритма также очевидно и выполняется с помощью математической индукции по k, показывая, что на k-й итерации вершина k включается в путь только тогда, когда новый путь имеет меньшую длинну.

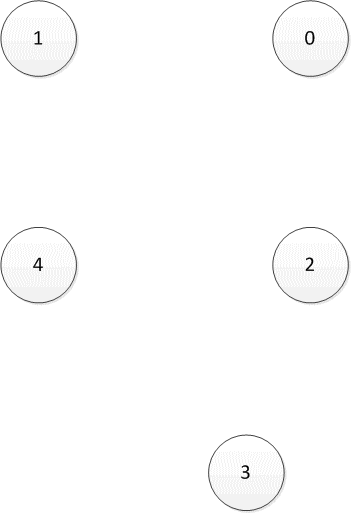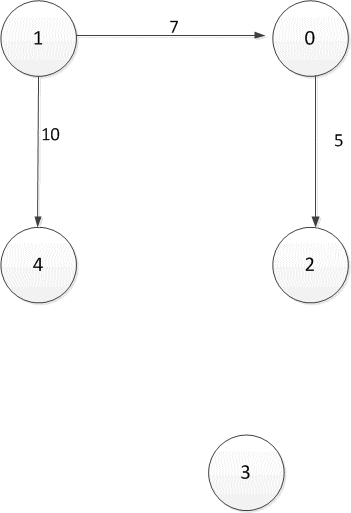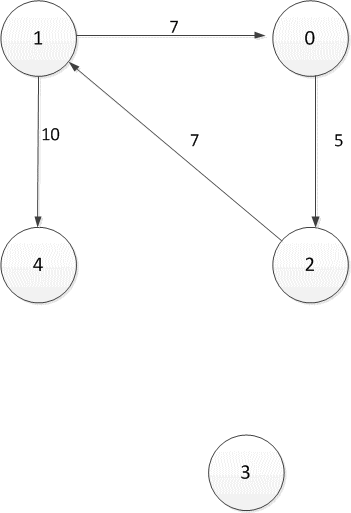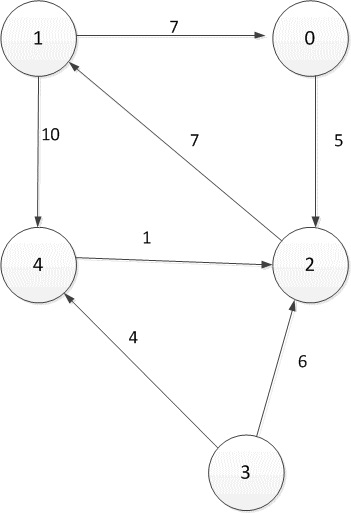
Рисунок 2.1 — Ориентированный направленный граф
(6 фреймов, 10 сек длительность, 11 kb)

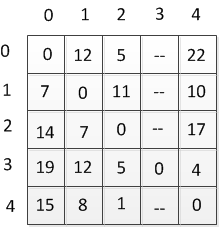
Таблица 2.1 — Таблица расстояний

2.2 Алгоритм Дейкcтры
Данный алгоритм находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса и широко применяется в программировании.
Суть алгоритма заключается в следующем. [3]
Имеется ориентированный граф G, который изображен на рисунке 2.2

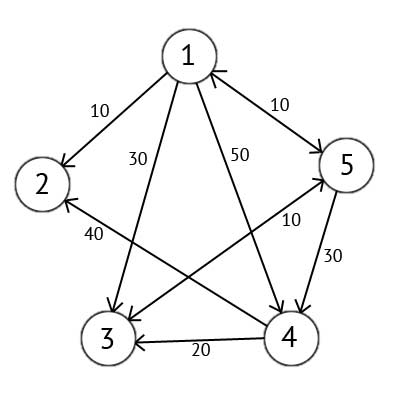
Рисунок 2.2 — Ориентированный граф G
Этот граф мы можем представить в виде матрицы С:

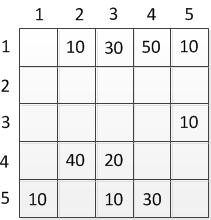
Таблица 2.2 — Матрица ориентированного графа

Выбираем вершину 1. Это означает, что будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5. Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере. Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.

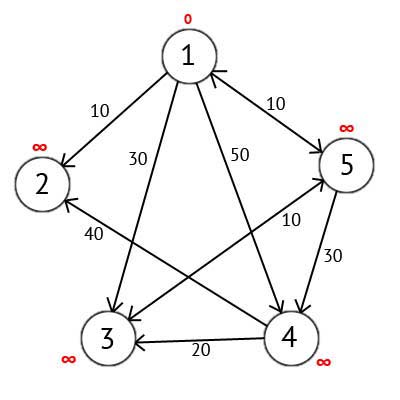
Рисунок 2.3 — Ориентированный граф после первого шага

Далее выберем такую вершину W, которая имеет минимальную метку и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.

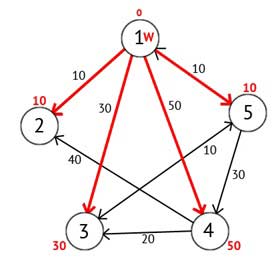
Рисунок 2.4 — Ориентированный граф после второго шага

Далее вершину W отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них можно выбрать как W.

Выберем вершину 2. Из нее нет ни одного исходящего пути, значит можно сразу отметить вершину как посещенную и перейти к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.

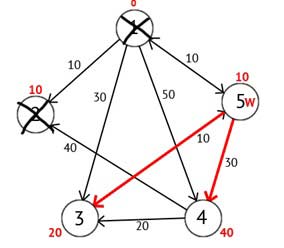
Рисунок 2.5 — Ориентированный граф после третьего шага

Исходя из рисунка 2.5 можно увидеть, что метки 3-ей и 4-ой вершин стали меньше, то есть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть не посещённые вершины.
Выполнив все действия, получим такой результат:

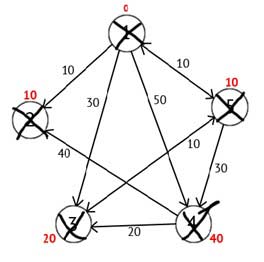
Рисунок 2.6 — Ориентированный граф на конечном шаге

3 Фильтр Калмана

Для улучшения качества сигнала необходимо проводить фильтрацию. Фильтрация — это алгоритм обработки данных, который убирает шумы и информацию, которая искажает полезность сигнала. Одним из распространенных фильтров является фильтр Калмана.

Фильтр Калмана — это алгоритм фильтрации, используемый во многих областях науки и техники. Его можно встретить в GPS-приемниках, интеллектуальных датчиках, в различных системах управления. Он использует динамическую модель системы. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):

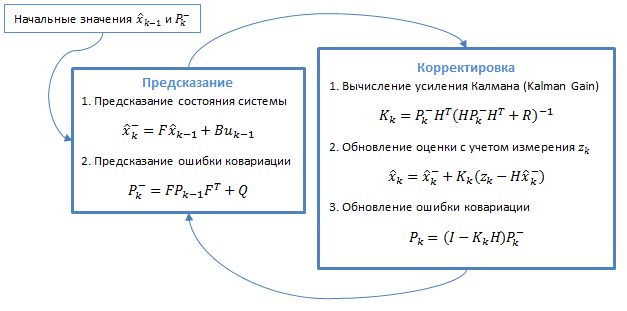
Рисунок 3.1 — Общий алгоритм фильтра

3.1 Модель динамической системы

Фильтры Калмана базируются на дискретизированных по времени линейных динамических системах. Состояние системы описывается вектором конечной размерности — вектором состояния. В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния (детерминированное изменение состояния), добавляется некоторый вектор нормального шума (случайные факторы) и в общем случае вектор управления, моделирующий воздействие системы управления.

При использовании фильтра Калмана для получения оценок вектора состояния процесса по серии зашумленных измерений необходимо представить модель данного процесса в соответствии со структурой фильтра — в виде матричного уравнения определенного типа. Для каждого такта k работы фильтра необходимо в соответствии с приведенным ниже описанием определить матрицы: перехода между состояниями F_k; матрицу измерений H_k; ковариационную матрицу шума процесса Q_k; ковариационную матрицу шума измерений R_k; при наличии управляющих воздействий — матрицу коэффициентов B_k.

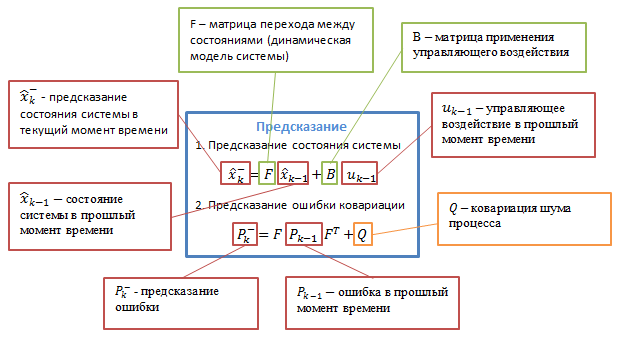
Рисунок 3.2 — Подробное описание алгоритма [9] x_k = F_kx_k-1 + B_ku_k + w_k, где F_k — матрица эволюции процесса/системы, которая воздействует на вектор x_k−1 (вектор состояния в момент k−1);
B_k — матрица управления, которая прикладывается к вектору управляющих воздействий u_k;
w_k — нормальный случайный процесс с нулевым математическим ожиданием и ковариационной матрицей Q_k, который описывает случайный характер эволюции системы/процесса: w_k ~ N(0,Q).
В момент k производится наблюдение (измерение) z_k истинного вектора состояния x_k, которые связаны между собой уравнением: z_k = H_kx_k + v_k, где
H_k — матрица измерений, связывающая истинный вектор состояния и вектор произведенных измерений, v_k — белый гауссовский шум измерений с нулевым математическим ожиданием и ковариационной матрицей R_k: v_k ~ N(0,R_k)

Фильтр Калмана является разновидностью рекурсивных фильтров. Для вычисления оценки состояния системы на текущий такт работы ему необходима оценка состояния (в виде оценки состояния системы и оценки погрешности определения этого состояния) на предыдущем такте работы и измерения на текущем такте. Данное свойство отличает его от пакетных фильтров, требующих в текущий такт работы знание истории измерений и/или оценок. Далее под записью X́_n|m будем понимать оценку истинного вектора x в момент n с учетом измерений с момента начала работы и по момент m включительно.

Ṕ_k|k — апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы (в русскоязычной литературе часто обозначается D́_k);
X́_k|k — апостериорная оценка состояния объекта в момент k полученная по результатам наблюдений вплоть до момента k включительно (в русскоязычной литературе часто обозначается X́_k, где X́ означает «оценка», а k – номер такта, на котором она получена).

В качестве движущегося объекта выберем судно, движение которого описывается системой дифференциальных уравнений: [8]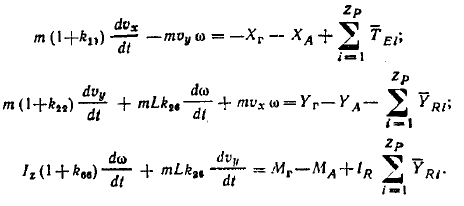

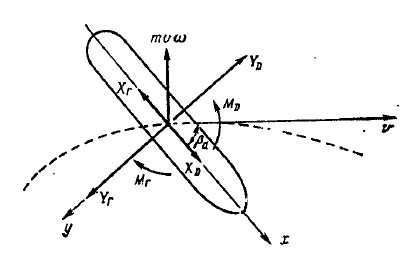
Рисунок 3.3 — Параметры модели судна.

4 Параллельные архитектуры

В настоящее время для повышения быстродействия вычислительных систем широко применяются различные подходы. Одним из них является использование многоядерных и многопроцессорных вычислительных архитектур. [1]

4.1 Параллелизм как основа высокопроизводительных вычислений

Многопроцессорные системы можно классифицировать следующим образом:
SISD (Single Instruction Single Data) – одиночный поток команд, одиночный поток данных (последовательные компьютеры фон Неймана). К этому классу относятся последовательные компьютерные системы, которые имеют один центральный процессор, способный обрабатывать только один поток последовательно исполняемых инструкций. Это обычные скалярные, однопроцессорные системы. [10]

SIMD ((Single Instruction Multiple Data) — характеризуются наличием одиночного потока команд, но множественного потока данных. К этому классу относятся однопроцессорные, векторно-конвейерные суперкомпьютеры.
Другим подклассом SIMD-систем являются векторные компьютеры. Векторные компьютеры манипулируют массивами сходных данных подобно тому, как скалярные машины обрабатывают отдельные элементы таких массивов. Это делается за счет использования специально сконструированных векторных центральных процессоров. [10]

MIMD — архитектура компьютера, которая используется для достижения высокопроизводительных параллельных вычислений. Особенность данной системы заключается в том, что вычислитель имеет несколько процессоров, которые функционируют асинхронно и независимо. Различные процессоры в любой момент могут выполнять различные команды над различными частями данных. MIMD архитектуры далее классифицируются в зависимости от физической организации памяти, то есть имеет ли процессор свою собственную локальную память и обращается к другим блокам памяти, используя коммутирующую сеть, или коммутирующая сеть подсоединяет все процессоры к общедоступной памяти. Исходя из организации памяти, различают следующие типы параллельных архитектур: Компьютеры с распределенной памятью (Distributed memory) Процессор может обращаться к локальной памяти, может посылать и получать сообщения, передаваемые по сети, соединяющей процессоры. Сообщения используются для осуществления связи между процессорами или, что эквивалентно, для чтения и записи удаленных блоков памяти. В идеализированной сети стоимость посылки сообщения между двумя узлами сети не зависит как от расположения обоих узлов, так и от трафика сети, но зависит от длины сообщения. [2]

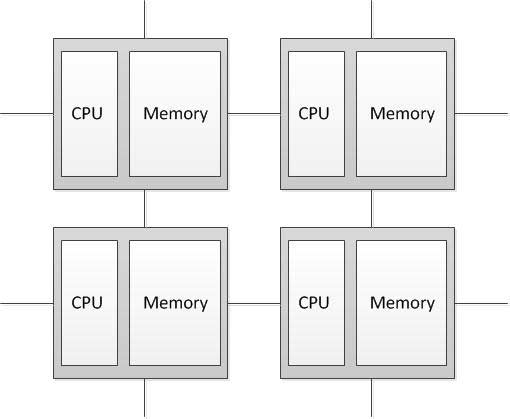
Рисунок 4.1 — Структура компьютера с распределенной памятью

4.2 Параллельные архитектуры GPU

Другой разновидностью параллельной архитектуры является графический процессор (англ. graphics processing unit, GPU), которое представляет собой отдельное устройство персонального компьютера, выполняющее графический рендеринг. Благодаря специализированной конвейерной архитектуре они намного эффективнее в обработке графической информации, чем типичный центральный процессор.

Для ускорения универсальных приложений используют совместную работу GPU и CPU для выполнения вычислений. Вычисления на GPU были изобретены компанией NVIDIA и быстро стали стандартом в индустрии, которую используют миллионы пользователей по всему миру и которую приняли практически все производители компьютерных систем.

CPU + GPU – система, которая увеличивает вычислительную мощность за счет того, что CPU состоят из нескольких ядер, оптимизированных для последовательной обработки данных, в то время как GPU состоят из тысячи ядер, созданных для параллельной обработки данных. Последовательные части кода обрабатываются на CPU, а параллельные части — на GPU.

Рисунок 4.2 — CPU+GPU [6]

5 Подходы и реализации

Параллельные архитектуры имеют свои особенности в реализации вычислений. Параллельное программирование применяется для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и CUDA. Параллельное программирование является более сложным по сравнению с последовательным как в написании кода, так и в его отладки.

5.1 MPI

MPI — программный интерфейс для передачи информации, который позволяет обмениваться сообщениями между процессами, выполняющими одну задачу. MPI является наиболее распространённым стандартом интерфейса обмена данными в параллельном программировании, существуют его реализации для большого числа компьютерных платформ. Используется при разработке программ для кластеров и супер компьютеров. Основным средством коммуникации между процессами в MPI является передача сообщений друг другу. В первую очередь MPI ориентирован на системы с распределенной памятью, то есть когда затраты на передачу данных велики. Базовым механизмом связи между MPI процессами является передача и приём сообщений. Сообщение несёт в себе передаваемые данные и информацию, позволяющую принимающей стороне осуществлять их выборочный приём: [7]
1. отправитель — ранг (номер в группе) отправителя сообщения;
2. получатель — ранг получателя;
3. признак — может использоваться для разделения различных видов сообщений;
4. коммуникатор — код группы процессов.

Операции приёма и передачи могут быть блокирующимися и не блокирующимися. Для не блокирующихся операций определены функции проверки готовности и ожидания выполнения операции.

5.2 CUDA

CUDA — программно-аппаратная архитектура параллельных вычислений, которая позволяет существенно увеличить вычислительную производительность благодаря использованию графических процессоров фирмы NVIDIA. [5]
В архитектуре CUDA используется модель памяти типа Grid, кластерное моделирование потоков и SIMD-инструкции. Ученые и исследователи широко используют CUDA в различных областях, включая астрофизику, вычислительную биологию и химию, моделирование динамики жидкостей, электромагнитных взаимодействий, компьютерную томографию, сейсмический анализ и многое другое. В CUDA имеется возможность подключения к приложениям, использующим OpenGL и Direct3D. CUDA — кросс платформенное программное обеспечение для таких операционных систем как Linux, Mac OS X и Windows.

6 Выводы

Актуальность использования супер компьютеров, а соответственно и параллельной архитектуры, при прогнозировании поведения движущегося объекта заключается в необходимости производить расчеты параметров движения объекта, его траектории пути и поведения в зависимости от внешних факторов за минимально возможное время

При прогнозировании модели поведения движущегося объекта крайне важна скорость вычисления, в связи с этим необходимо повышать эффективность этих вычислений. Это является основной и актуальной задачей.

Список источников

1. Parallel Computer Architecture: A Hardware/Software Approach (The Morgan Kaufmann Series in Computer Architecture and Design), Callifornia, 1999, 1025c
2. MIMD–архитектура. Электронный ресурс. Режим доступа:
http://www.ccas.ru/paral/mimd/mimd.html
3. Алгоритм Дейкстры. Электронный ресурс. Режим доступа:
http://habrahabr.ru/post/111361/
4. Алгоритм Флойда-Уоршелла. Электронный ресурс. Режим доступа:
http://urban-sanjoo.narod.ru/floyd.html
5. CUDA. Электронный ресурс. Режим доступа:
http://www.nvidia.ru/object/what_is_cuda_new_ru.html
6. CUDA Parallel Computing Platform. Электронный ресурc. Режим доступа: http://www.nvidia.com/object/cuda_home_new.html
7. Message Passing Interface Forum. Электронный ресурс. Режим доступа:
http://www.mpi-forum.org/
8. Ходкость и управляемость судов. Под ред. В.Г. Павленко. М.: Транспорт, 1991., с. 318.
9. Фильтр Калмана. Электронный ресурс. Режим доступа:
http://habrahabr.ru/post/140274/
10. SIMD и SISD. Электронный ресурс. Режим доступа:
http://rudocs.exdat.com/docs/index-43961.html?page=13