Українська   English
ДонНТУ   Портал магистров

Содержание

Введение

Добыча природного минерального сырья создает материальную базу промышленного производства, удовлетворяя потребности общества в металлах, топливе, строительных и химических материалах. Значительная часть полезных ископаемых добывается на предприятиях с подземными горными работами, что предполагает широкое применение шахтных подъемных установок для транспортировки горной массы на поверхность.

Подъемные установки являются одним из основных элементов транспорта на горных предприятиях. Надежность и высокая производительность шахтного подъема во многом определяет эффективную работу предприятия в целом.

Первая крупная отечественная подъемная машина была построена в 1935 г. В настоящее время наиболее перспективными конструкциями являются многоканатные подъемные машины со шкивами трения. Проблема подъема больших грузов со значительной глубины успешно решается применением многоканатного подъема. Шахтные подъемные установки, являясь крупнейшими транспортными устройствами, обладают специфическими, присущими только им, особенностями: огромной массой подъемной системы в целом, перемещаемой в условиях неустановившегося режима движения со значительными ускорениями; значительной массой подъемных канатов. Эти факторы превращают отрицательное влияние массы и инерции составных частей подъемной системы в большую проблему, так как значительная масса концевого груза приводит к увеличению размеров электромеханической части подъема, а неуравновешенность и инерция движущихся масс ухудшает его энергетические показатели.

Большие массы шахтной машины, движущиеся с большими скоростями, вызывают сложные динамические процессы при пусках и торможениях. Динамические процессы формируют чрезмерные нагрузки, прогрессирующие усталостные явления отдельных элементов конструкции, которые приводят к аварийным ситуациям и к катастрофам.

Для увеличения надежности, безопасности и долговечности машин проектирование и изготовление их должно осуществляться с учетом воздействия динамических усилий. Теоретическим фундаментом динамических расчетов является теория механических колебаний. Знания законов колебательных процессов позволяют спроектировать рациональные конструкции машин.

1. Актуальность темы

Вопросам совершенствования подъемных установок и разработки теории рудничного подъема уделялось первостепенное внимание на протяжении всей истории развития добычи полезных ископаемых подземным способом. Однако, несмотря на долгую и богатую историю развития темы, практика проектирования и эксплуатации подъемных установок показывает, что технические возможности выбранного оборудования часто остаются недоиспользованными, а размеры и вес оборудования завышенными.

Поэтому актуальной остается задача совершенствования методов расчета и проектирования динамических режимов шахтных подъемных установок с целью обеспечения рациональных технических характеристик.

Построение математических моделей работы подъемной установки позволит в дальнейшем более детально изучить работу ее отдельных узлов для выбора их оптимальных характеристик. Что в свою очередь позволит повысить безопасность подъемной установки, а это особенно важно при рассмотрении пассажирских установок, оптимизировать скоростные характеристики ШПУ, а также изучить износ оборудования от динамических усилий для последующего устранения имеющихся проблем.

2. Цель и задачи исследования

Целью данной работы является математическое моделирование динамических процессов одноконцевой и двухконцевой подъемных машин с канатами большой длины.

Основные задачи моделирования:

  1. Вывод уравнений движения для двух типов машин.
  2. Определение рационального числа упругих масс каната.
  3. Моделирование рабочего режима подъемной машины.

3. Обзор исследований и разработок

Промышленное производство и технический прогресс немыслимы без такой науки, как механика. Одним из важнейших разделов механики является динамика.

    3.1 История развития динамики машин

Основоположником динамики машин можно считать петербуржского академика Э. Л. Эйлера (1707–1783). В своих работах Эйлер впервые выделил силы сопротивления, преодолеваемые машиной в движении – он разделил их на силы инерции и силы трения [1]. Выведенная им формула, получившая название формулы Эйлера, по сей день широко используется для исследования процессов трения канатов по футеровке барабана многоканатных подъемных машин.

Представитель французской школы механиков Ж. Даламбер (1717–1783) попытался дать общую методику решения задач динамики [2]. В своих работах по аналитической механике Ж. Лагранж (1736–1813) развил принцип Даламбера и разработал общую методику решения задач динамики и статики аналитическим путем[2].

В ходе истории развитие техники представляло перед учеными все более новые и интересные задачи. В частности, задачи динамики механических систем с распределенной массой.

Российский ученый А. М. Ляпунов (1857–1918) впервые исследовал проблему устойчивости механических систем с конечным числом степеней свободы [3]. А. Н. Крылов (1863–1945), исследуя колебания поршня индикатора паровой машины, решил задачу колебания массы груза, прикрепленного к концу стержня [3]. Решения подобных задач используется при исследовании вязкоупругих систем с распределенными параметрами, представителями которых являются шахтные подъемные установки.

Вопросами исследования и уменьшения динамических нагрузок в канатах шахтных подъемников в ХХ веке занимались такие ученые, как А. И. Динник, С. П. Тимошенко, М. М. Федоров, Ф. В. Флоринский, Г. Н. Савин, А. Н Голубенцев, Л. В. Колосов и др.

Для изучения и определения динамических нагрузок в подъемниках зачастую их рассматривали как многомассовую механическую систему с упругими связями.

Основополагающими исследованиями динамики подъемного каната являются работы академика А. Н. Динника (1876–1950) [4]. Созданная акад. А. Н. Динником лаборатория механических испытаний материалов стала в Украине центром испытания стальных канатов и другого горного оборудования. А. Н. Динник создал научные школы в области теории и расчета подъемных канатов, устойчивости форм и упругого равновесия, учения о давлении горных пород. Рассматривая канат как гибкую нить, А. Н. Динник для изучения продольных колебаний канатов с концевым грузом впервые рассмотрел канат как континуальную упругую систему [5–7]. Коэффициенты устойчивости, вычисленные им, вошли в справочную литературу. Рассмотрев в первом приближении горную породу как упругую изотропную среду и применив методы теории упругости, А. Н. Динник определил закон распределения и величину напряжений в горных выработках.

Всемирное признание получил академик С. П. Тимошенко (1878–1972) [8–10]. Он показал, что для невесомого каната, один конец которого защемлен (неподвижен), а на другом висит груз, частота колебаний груза будет практически одинакова системе весомый канат – груз, если рассматривать канат как невесомый стержень и к грузу прибавить одну треть массы каната. Этот результат адекватен прибавлению одной трети массы каната от узла колебаний, то есть от точки, амплитуда колебаний которой равна нулю.

Академик М. М. Федоров (1867–1945) исследованиями в области шахтного подъема создал новую научную дисциплину, которая получила название – горная механика. Он вывел основное динамическое уравнение рудничных подъёмных установок с постоянным радиусом навивки; предложил гармонический подъём, обеспечивший полное динамическое уравновешивание подъёмных установок с тяжёлым хвостовым канатом [11].

Ф. В. Флоринский (1905–1975) обобщил теоретические исследования многих ученых и предложил новые методы расчета весомого подъемного каната в виде простых формул и таблиц. Созданная Ф. В. Флоринским динамическая теория расчета шахтных подъемных канатов до настоящего времени является научной основой дальнейших работ в этой области. Им рассмотрены задачи динамики каната как весомого упруго–вязкого стержня с грузом на конце при условии, когда верхней конец каната имеет ускорение [12].

Ряд работ Г. Н. Савина (1907–1975) были посвящены исследованию задач динамики нити (каната) переменной длины. Они составляли основу предложенной им новой теории расчета шахтных подъемных канатов, в которых учитывался динамический режим их работы [13, 14].

Голубенцев А. Н. (1916–1971) разработал теорию переходных процессов в машинах с упругими звеньями и получил новые существенные результаты по оптимизации процессов в пространстве параметров машин. Им были изложены основы динамики переходных процессов в линиях передач тяжелых машин с учетом упругости их звеньев. Были подробно рассмотрены колебательные явления в шахтных подъемных машинах, а так же дано понятие о синтезе машин в целях получения наиболее благоприятного переходного процесса на основе применения наилучшего приближения Чебышева. Для расчетов переходных процессов Голубенцев А. Н. применял метод главных координат, что позволяло получать замкнутые решения в случае сложных многомассовых систем, пользуясь простейшими классическими методами решения дифференциальных уравнений [15].

Л. В. Колосов (1936–2000) являлся продолжателем научной школы теории и расчета шахтных подъемных канатов, сформированной А. Н. Динник и Ф. В. Флоринским. Л. В. Колосов исследовал динамику стальных канатов в условиях их взаимодействия с подъемной машиной. Под руководством Л. В. Колосова было создано новое научное направление по расчету и конструированию плоских резинотросовых канатов, разработана теория расчета этих канатов, их конструкции, техническая документация по изготовлению и эксплуатации [16, 17].

    3.2 Динамика подъема в наши дни

Современное состояние вопроса о динамических нагрузках в подъемых машинах описано в работах таких выдающихся ученых, как Р. Л. Мищенко, В. И. Дворников, А. Г. Степанов и др.

Профессор В. И. Дворников в своих работах освещал основы теории и динамики шахтного подъема. Им были разработаны методы эффективной эксплуатации, диагностики и ремонта подъемных машин, редукторов, тормозных устройств, подъемных сосудов, приводов постоянного и переменного тока и другого оборудования, обобщен опыт повышения надежности в процессе эксплуатации.

Однако большую значимость для данной работы имеют труды В. И. Дворникова непосредственно по динамической теории расчета шахтных подъемных канатов [18–20].

В своих работах автор представляет базисную модель двухконцевой шахтной подъемной установки в вертикальном стволе в виде трехмассовой системы сосредоточенных тел, соединенных между собой массивными канатами, как это изображено на рис. 1 [20].

Схематизация одноконцевой подъемной установки

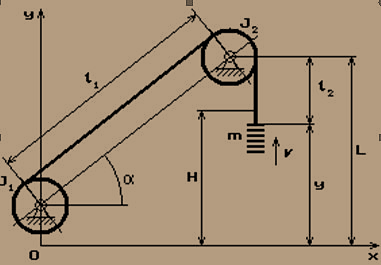
Рисунок 1 – Схематизация одноконцевой подъемной установки

Определение динамических переменных и динамических силовых факторов такой базисной модели сводится автором к алгоритму:

  1. Находится необходимое количество собственных частот.
  2. Каждому найденному значению частоты приводятся в соответствие трехкомпонентная матрицa-столбец форм, предварительно вычислив коэффициенты динамических жесткостей.
  3. Интегрируются уравнения координатных функций параллельно с вычислениями эрмитовых форм.
  4. Используются разложение по собственным формам общего решения уравнения для вычислений перемещений скоростей и ускорений грузов и барабана машины и определения динамических усилий в канатах.

Подъемный канат представлен Дворниковым В. И. в виде упругой невесомой нити. Масса каната приведена к сосредоточенной массе сосуда. Справедливость данного допущения зависит от длины уравновешивающего каната. При малой длине уравновешивающего каната его распределенная масса оказывает несущественное влияние на динамические процессы. Выполненные исследования для существующих неуравновешенных подъемных установок, при принятых допущениях, дают значение частотных и амплитудных величин, которые сравнимы с решением этой задачи в частных производных. В ущерб более строгим представлениям принятие этого допущения существенно уменьшает трудоемкость решения. Однако при больших длинах каната появляются большие погрешности в определении динамических усилий в канатах. Для того, чтобы избежать больших погрешностей, распределенную массу этого каната рекомендуется разбить на несколько равных масс, соединенных невесомыми вязкоупругими связями.

Динамикой подъемных машин с подобным учетом распределенной массы упругих элементов занимался доктор технических наук, профессор Степанов А. Г. [21–24]. В своих работах он предлагает эквивалентную схему, в которой головные и уравновешивающие канаты разбиты на некоторое количество частей, представляющих собой массы, соединенные вязкоупругими связями (рис. 2). Однако в рассматриваемых работах отсутствуют рекомендации по выбору количества масс, на которые следует разбивать канат заданной длины.

Эквивалентная схема ветви канатов уравновешенного подъема

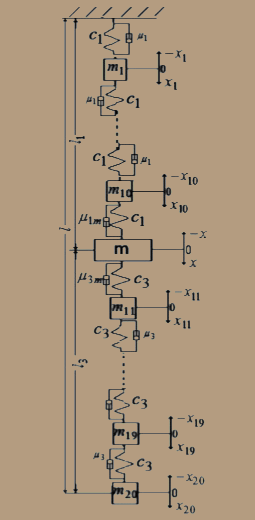
Рисунок 2 – Эквивалентная схема ветви канатов уравновешенного подъема

Однако такой способ определения динамических нагрузок в канате представляется сложным по той причине, что для моделирования динамических процессов необходима достаточно мощная вычислительная техника.

Учитывая теоретические исследования выше приведенных авторов, автор данной работы предлагает заменить канат большой длины некоторым количеством распределенных упругих диссипативных масс.

4. Математическое моделирование динамических процессов в одноконцевой подъемной машине с канатами большой длины

Подъем груза в вертикальном стволе будет происходить согласно схеме, показанной на рис. 3.

Подъем груза с помощью одноконцевой подъемной машины

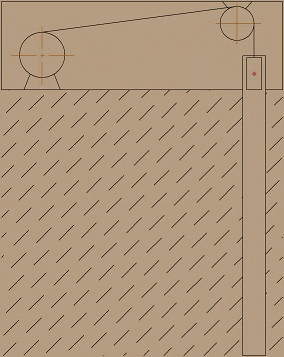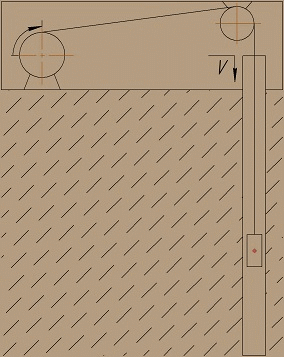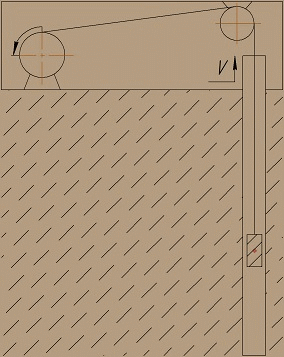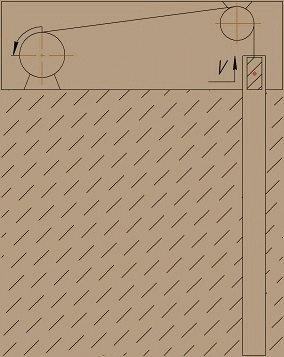
Рисунок 3 – Подъем груза с помощью одноконцевой подъемной машины
(анимация: 8 кадров, 5 циклов повторения, 142 килобайт)

Такая машина состоит из барабана машины с приведенными к нему моментами инерции вращающихся частей редуктора и ротора электродвигателя с кинетическим моментом инерции Jб, направляющего шкива с моментом инерции Jш, наклонной струны каната lcтр, считающейся неизменяющейся во времени, и отвесной части каната lотв, на которой закреплена масса концевого груза mn (рис. 4).

Схематическая модель одноконцевой подъемной машины

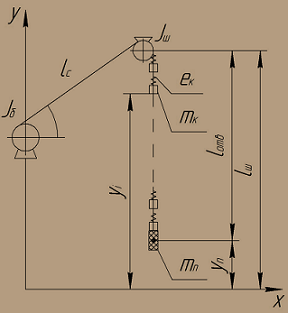
Рисунок 4 – Схематическая модель одноконцевой подъемной машины

Отвесный канат подъемной машины разбит на некоторое количество распределенных масс mk с координатами yi, связанных между собой упругими связями ek. Концевой груз mn имеет перемещение yn по вертикали, отсчитываемое от некоторого исходного положения груза.

Для некоторого упрощения вывода уравнений движения примем следующие допущения:

  1. Считаем функции, зависимые от времени, медленно изменяющимися. Концепция медленно изменяющихся функций позволяет рассматривать систему как адиабатическую, то есть как систему с якобы постоянными коэффициентами, а затем в полученных решениях уже учесть их фактическую «медленную» зависимость от времени. Вследствии этого примем, что коэффициент податливости первого элемента е1 остается неизменной.
  2. Так как моделирование будет проходить в течении сравнительно небольшого участка времени, то можно принять, что за это время количество масс каната не поменяется.

Для вывода уравнений динамики машины используем уравнения Лагранжа ІІ рода:

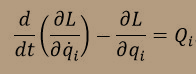Уравнения Лагранжа.

Так как сила сопротивления участков каната пропорциональна скорости движения, то на каждый участок дополнительно будут действовать диссипативные силы. С учетом функции Рэлея уравнения Лагранжа ІІ рода примут вид:

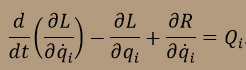Уравнения Лагранжа и Рэлея.

Кинетическая энергия такой системы будет состоять из суммы кинетических энергий трех рассматриваемых сосредоточенных масс, струны и отвеса и примет вид:

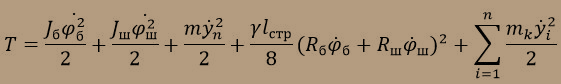Кинетическая энергия системы.

Потенциальная энергия будет состоять из потенциальной энергии сил упругой деформации струны и отвеса при принятых допущениях и гравитационной части с учетом, что струна наклонена к горизонту под углом:

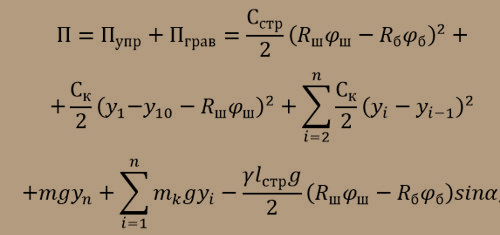Потенциальная энергия системы.

где: Сстр – коэффициент жесткости струны, Ск – коэффициент жесткости i–ой части отвеса, y1 – положение первой упруго–диссипативной массы отвеса, y10 – начальное положение первой массы.

Функция Лагранжа представляет собой разность кинетической и потенциальной энергий системы и для данного случая будет иметь вид:

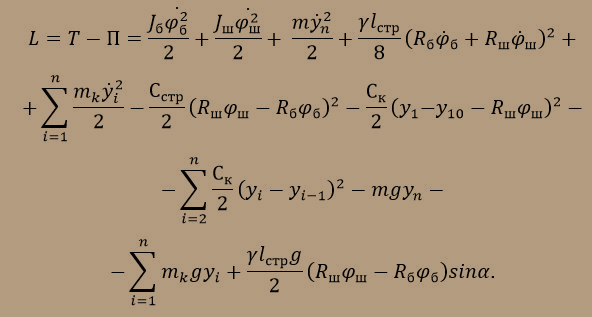Функция Лагранжа.

Определим в качестве обобщенных координат элементов рассматриваемой системы переменные

Обобщенные координаты,

тогда соответственно в качестве обобщенных скоростей

Обобщенные скорости.

Обобщенные непотенциальные силы Q1, Q2, Qi (i=1...n) для рассматриваемой системы примем следующими: Q1=Mдв(t), Q2=0, Qi=0 (i=1...n), где Mдв(t) – приведенный к оси барабана момент, развиваемый двигателем, и эту переменную будем считать известной функцией от времени.

Обобщенные силы Q2, Qi (i=1...n) приняты равными нулю, так как предполагается, что шкив и концевой груз не подвержены действию иных внешних сил, кроме уже учтенных.

Произведя необходимые вычисления производных от функции Лагранжа, в итоге получим искомые уравнения движения:

Уравнения движения.

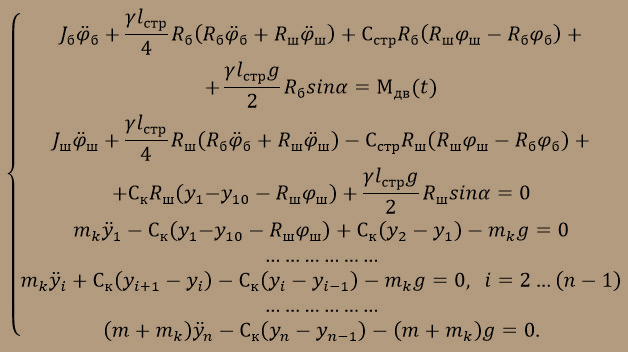Поскольку упругие и диссипативные элементы связей располагаются параллельно, то при учете диссипативных сил, не записывая выражение для функции Рэлея, легко получить итоговую математическую модель рассматриваемой динамической системы путем добавления диссипативных составляющих:

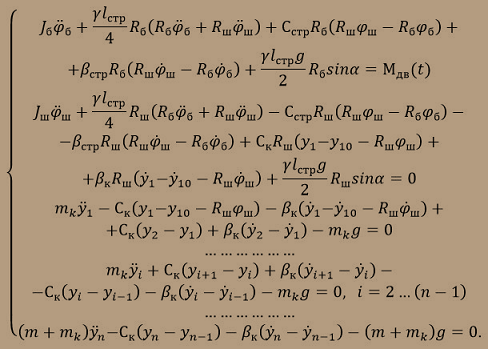Уравнения движения.

Выводы

Полученные уравнения движения позволяют проследить упругие и гравитационные воздействия, действующие на барабан, шкив, груз, а также на каждый отрезок каната во время пуска машины, ее работы и торможения. Такую методику определения динамических усилий в канате можно применять для любых одноконцевых подъемных машин.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2015 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Euler L. De machinis in genere. Novi Commentarii Acad. Sci. Imp. Petrop., 3, 1753. – P. 254-285.
  2. Стройк Д. Я. Краткий очерк истории математики / Д. Я. Стройк. – М. : Наука, 1984. – 283 с.
  3. Осецкий В. М. Техническая механика / В. М. Осецкий – М. : Госгортехиздат, 1962. – 471 с.
  4. Динник А. Н. Динамические напряжения в подъемном канате при внезапной остановке верхнего конца / А. Н. Динник. – Южный инженер, 1917. – № 3-4.
  5. Динник А. Н. Кручение. Теория и приложение / А. Н. Динник. – М., 1938.
  6. Динник, А. Н. Устойчивость упругих систем : учеб. пособие для ун-тов / акад. А. Н. Динник, проф. Днепропетр. металлург. ин-та. – М. : ОНТИ НКТП СССР, Гл. ред. общетехн. лит. и номографии, 1935. – 183 с.
  7. Кожухов А. А., Очинский В. В. Академик А. Н. Динник (к 130-летию со дня рождения) // Исследования по истории физики и механики 2006. – М.: Наука, 2007. – С. 239-248.
  8. Тимошенко С. П. Колебания в инженерном деле / С. П. Тимошенко, Д. Х. Янг, У. Уивер ; пер. с англ. Л. Г. Корнейчука. – М. : Машиностроение, 1985. – 472 с.
  9. Тимошенко С. П. О вынужденных колебаниях призматических стержней / С. П. Тимошенко. – Киев: тип. С. В. Кульженко, 1909. – 50 с.
  10. Тимошенко С. П. Статистические и динамические проблемы теории упругости / С. П. Тимошенко. – Киев: Наукова думка, 1975. – 564 с.
  11. Федоров М. М. Методология динамической теории расчета подъемного каната вертикальных шахт / М. М. Федоров // Записки института горной механики. АН УССР. – 1936. – № 1.
  12. Флоринский Ф. В. Динамика шахтного подъемного каната / Федор Валентинович Флоринский. – М. : Углетехиздат, 1955. – 238 с.
  13. Савин Г. Н. Динамическая теория расчета шахтных подъемных канатов / Г. Н. Савин. – К. : Из-во АН УССР, 1949. – 238 с.
  14. Савин Г. Н. Динамика нити переменной длины / Г. Н. Савин, О. А. Горошко. – К. : Из-во АН УССР, 1949. – 332 с.
  15. А. Н. Голубенцев, Динамика переходных процессов в машинах со многими массами / А. Н. Голубенцев. – Москва: ГНТИ, 1959.
  16. Колосов Л. В., Потураев В. Н., Червоненко А. Г., Безпалько В. В., Завозин Л. Ф. Вертикальный транспорт на горных предприятиях / Л. В. Колосов, В. Н. Потураев , А. Г. Червоненко, В. В. Безпалько, Л. Ф. Завозин. – М.: Недра, 1975. – 350с.
  17. Гаркуша Н. Г., Колосов Л. В., Обухов А. Н. и др. Подвесные устройства шахтных подъемных сосудов. Под ред. Н. Г. Гаркуши / Н. Г. Гаркуша, Л. В. Колосов, А. Н. Обухов. – М.: Недра, 1980. – 105 с.
  18. Дворников В. И. Теоретические основы динамики шахтного подъемного комплекса / В. И. Дворников, Е. Р. Къерцелин. – София, МОНТ, 1997. – 363 с.
  19. Дворников В. И., Къерцелин Е. Р., Трибухин В. А., Савенко Э. С. Динамические жесткости канатов шахтных подъемных установок / В. И. Дворников, Е. Р. Къерцелин, В. А. Трибухин, Э. С. Савенко // Стальные канаты. – Одесса, 2003. – Вып. 3.
  20. Шахтный подъем: Научно–производственное издание / В. Р. Бежок, В. И. Дворников, И. Г. Манец, В. А. Пристром; общ. ред. Б. А. Грядущий, В. А. Корсун. – Донецк : ООО «Юго-Восток Лтд», 2007. – 624 с.
  21. Степанов А. Г. Динамика шахтных подъёмных установок / Анатолий Григорьевич Степанов. – Пермь : УрО РАН, 1994. – 263 с.
  22. Степанов А. Г. Динамика машин / А. Г. Степанов. – Екатеринбург: Российская академия наук, 1999. – 392 с.
  23. Степанов А. Г., Корняков М. В. Динамика машин : монография. 2–е изд., испр. и доп. / А. Г. Степанов, М. В. Корняков. – Иркутск : Изд-во ИрГТУ, 2014. – 412 с.
  24. Степанов А. Г. Динамические процессы при скольжении канатов по футеровке барабана многоканатной подъемной установки / А. Г. Степанов // Горное оборудование и электромеханика. № 6, 2010. – C. 24-35.