A signal assignment schedules one or more transactions to a signal (or port). The syntax of a signal assignment is:
signal_assignment_statement ::= target <= [ transport ] waveform ;
target ::= name | aggregate
waveform ::= waveform_element { , waveform_element }
waveform_element ::=
value_expression [ after time_expression ]
| null [ after time_expression ]
The target must represent a signal, or be an aggregate of signals (see also variable assignments, Section 2.4.1). If the time expression for the delay is omitted, it defaults to 0 fs. This means that the transaction will be scheduled for the same time as the assignment is executed, but during the next simulation cycle.
Each signal has associated with it a projected output waveform, which is a list of transactions giving future values for the signal. A signal assignment adds transactions to this waveform. So, for example, the signal assignment:
s <= '0' after 10 ns;
will cause the signal enable to assume the value true 10 ns after the assignment is executed. We can represent the projected output waveform graphically by showing the transactions along a time axis. So if the above assignment were executed at time 5 ns, the projected waveform would be:
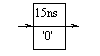
When simulation time reaches 15 ns, this transaction will be processed and the signal updated.
Suppose then at time 16 ns, the assignment:
s <= '1' after 4 ns, '0' after 20 ns;
were executed. The two new transactions are added to the projected output waveform:
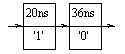
Note that when multiple transactions are listed in a signal assignment, the delay times specified must be in ascending order.
If a signal assignment is executed, and there are already old transactions from a previous assignmenton the projected output waveform, then some of the old transactions may be deleted. The way this is done depends on whether the word transport is included in the new assignment. If it is included, the assignment is said to use transport delay. In this case, all old transactions scheduled to occur after the first new transaction are deleted before the new transactions are added. It is as though the new transactions supercede the old ones. So given the projected output waveform shown immediately above, if the assignment:
s <= transport 'Z' after 10 ns;
were executed at time 18 ns, then the transaction scheduled for 36 ns would be deleted, and the projected output waveform would become:
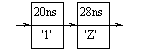
The second kind of delay, inertial delay, is used to model devices which do not respond to input pulses shorter than their output delay. An intertial delay is specified by omitting the word transport from the signal assignment. When an inertial delay transaction is added to a projected output waveform, firstly all old transactions scheduled to occur after the new transaction are deleted, and the new transaction is added, as in the case of transport delay. Next, all old transactions scheduled to occur before the new transaction are examined. If there are any with a different value from the new transaction, then all transactions up to the last one with a different value are deleted. The remaining transactions with the same value are left.
To illustrate this, suppose the projected output waveform at time 0 ns is:
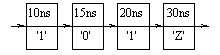
and the assignment:
s <= '1' after 25 ns;
is executed also at 0 ns. Then the new projected ouptut waveform is:
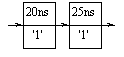
When a signal assignment with multiple waveform elements is specified with intertial delay, only the first transaction uses inertial delay; the rest are treated as being transport delay transactions.