

Саенко Ольга Сергеевна
Факультет Компьютерных информационных технологий и автоматики
Группа АТ-98а
ДИССЕРТАЦИЯ
на тему: "Разработка алгоритмов управления шестиногим шагающим аппаратом
на основе специальных и особопроходимых походок"
Научный руководитель: доц. кафедры АТ, к.т.н. Рафиков Г.Ш.

- АКТУАЛЬНОСТЬ РАБОТЫ
- ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ
- УРАВНЕНИЯ ДВИЖЕНИЯ ША В РЕЖИМЕ БЕГА
- Математическая модель движения аппарата
- Построение программного движения аппарата
- Стабилизация движения ША в режиме бега
- УРАВНЕНИЯ ДВИЖЕНИЯ ША В РЕЖИМЕ ПРЫЖКОВ
- Математическая модель движения аппарата в фазе опоры
- Программное движение ША в фазе опоры
- Математическая модель движения ША в фазе полета
- Построение программного движения аппарата в фазе полета
- Стабилизация аппарата в фазе полета
- Экспериментальные исследования особопроходимых походок путем моделирования их на ПЭВМ
- Моделирование специальных походок в режиме бега
- Моделирование специальных походок в режиме прыжка
- Перечень ссылок
- АПРОБАЦИЯ РЕЗУЛЬТАТОВ
- ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫ ИССЛЕДОВАНИЯ

АКТУАЛЬНОСТЬ РАБОТЫ
С увеличением числа ног шагающего аппарата (ША) расширяется область
статически устойчивой ходьбы, однако большее число ног приводит к усложнению управления.
Результаты исследований [1] показывают, что при увеличении скорости статически устойчивое
передвижение не будет достаточно эффективным, так как потребует соответственно повышения
скорости переноса ног. Поэтому на высоких скоростях целесообразно переходить к динамическим
режимам движения, аналогично тому, как это имеет место у животных. Это объясняет возросший
интерес к разработке алгоритмов управления движением аппаратов, перемещающихся в рамках
динамической устойчивости. Бег является статически неустойчивым в любой фазе
движения. Движение прыжками является статически устойчивым в фазе опоры и неустойчивым в фазе
полета. Понятие динамической устойчивости можно также определить как периодическую
устойчивость, когда система в конце цикла восстанавливает свое первоначальное состояние.
В данной работе исследуется ША как система с периодически устойчивым движением. Использование
подобных режимов движения ША увеличивает его проходимость, делает способным преодолевать
препятствия, а также целесообразно в смысле экономии суммарных затрат энергии на организацию
движения.
ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ
Целью работы является
1. Исследование пространственное движение шагающего аппарата с невесомыми ногами, перемещающегося
в режиме бега и прыжков.
2. Получение математической модели динамики движения в режиме бега и прыжков.
3. Решение задачи построения программного движения и стабилизации движения аппарата.
4. Проведение экспериментальных исследований на ПЭВМ при помощи пакета прикладных программ
MATLAB 6.0. и Sumulink 4.0, доказывающих работоспособность синтезированных алгоритмов движения
и стабилизации аппарата при наличии различного рода возмущений.
УРАВНЕНИЯ ДВИЖЕНИЯ ША В РЕЖИМЕ БЕГА
Математическая модель движения аппарата
Рассматривается аппарат, состоящий из массивного корпуса и четырех одинаковых невесомых ног.
С корпусом аппарата связана декартова правая система координат Oxyz (рис. 1), оси которой
направлены вдоль главных осей инерции корпуса. Положение корпуса относительно осей абсолютной
системы координат
 (плоскость
(плоскость
 - горизонтальна) определяется
координатами центра масс корпуса
- горизонтальна) определяется
координатами центра масс корпуса
 и углами
и углами
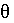 - рыскания,
- рыскания,
 - тангажа,
- тангажа,
 - крена.
ША движется осью Оу вперед. Ось Оz является конструктивной вертикалью корпуса.
- крена.
ША движется осью Оу вперед. Ось Оz является конструктивной вертикалью корпуса.
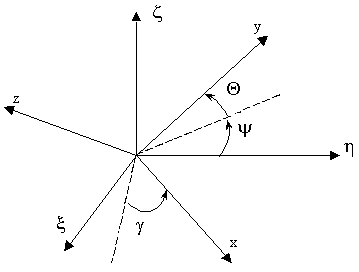
Рисунок 1 - Связь между абсолютной системой координат и системой, связанной с аппаратом
Движение корпуса аппарата описывается уравнениями движения твердого тела (корпуса) под
действием силы тяжести, сил реакции опорной поверхности в точках опоры ног и возмущающих
сил. Математическая модель описывается следующими выражениями:
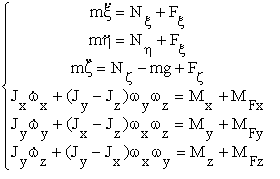 , (1)
, (1)
где
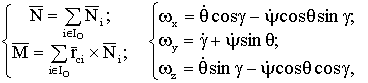 , (2)
, (2)
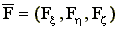 - возмущающие силы;
- возмущающие силы;
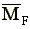 - момент возмущающих сил относительно
центра масс корпуса;
- момент возмущающих сил относительно
центра масс корпуса;
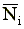 - реакции в точках опоры ног;
- реакции в точках опоры ног;
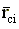 - радиус-вектор стопы i-той ноги
в системе координат Oxyz;
- радиус-вектор стопы i-той ноги
в системе координат Oxyz;
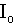 - множество индексов опорных ног в
текущий момент времени;
- множество индексов опорных ног в
текущий момент времени;
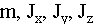 - масса и главные моменты инерции корпуса.
Величина возмущающих сил
- масса и главные моменты инерции корпуса.
Величина возмущающих сил
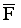 и их момента относительно центра масс
и их момента относительно центра масс 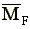 не
известна системе управления движением аппарата. При решении задач построения программного
движения и стабилизации движения аппарата
не
известна системе управления движением аппарата. При решении задач построения программного
движения и стабилизации движения аппарата
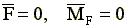 . (3)
. (3)
Построение программного движения аппарата
Исследуется бег аппарата парными походками
(рысь, иноходь и галоп) по горизонтальной плоскости.
После каждой фазы опоры на две ноги (длительность этой фазы
 ) следует фаза полета.
Одну опорную фазу движения и следующую за ней фазу полета будем называть шагом.
Продолжительность фазы полета
) следует фаза полета.
Одну опорную фазу движения и следующую за ней фазу полета будем называть шагом.
Продолжительность фазы полета
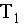 не меняется от шага к шагу. Программное движение обеспечивает равномерность нагрузки в
опорной фазе на обе опорные ноги и строится так, что в проекции на горизонтальную
поверхность центр масс аппарата движется равномерно и прямолинейно [2]
не меняется от шага к шагу. Программное движение обеспечивает равномерность нагрузки в
опорной фазе на обе опорные ноги и строится так, что в проекции на горизонтальную
поверхность центр масс аппарата движется равномерно и прямолинейно [2]
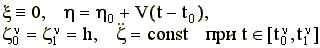 , (4)
, (4)
где V - скорость движения аппарата, t - текущее время,
 - момент начала опорной фазы
- момент начала опорной фазы
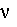 -го шага,
-го шага,
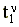 - момент начала фазы полета,
- момент начала фазы полета,
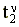 - момент окончания
- момент окончания
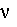 -го шага,
h - клиренс.
-го шага,
h - клиренс.
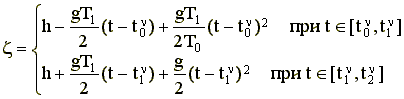 . (5)
. (5)
Таким образом, учитывая (1)-(5) получаем
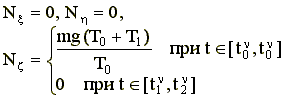 . (6)
. (6)
Стабилизация движения ША в режиме бега
Алгоритм стабилизации движения аппарата обеспечивает реализацию построения программного
движения аппарата при наличии различного рода возмущений. В фазе полета аппарат движется
под действием силы тяжести и возмущающих сил и его движение не управляемо. В опорной фазе
стабилизация движения аппарата осуществляется за счет изменения реакций в точках опоры ног
(управляющих усилий в степенях подвижности ног) и варьирования координат точек постановки
ног на опорную поверхность для последующих шагов (изменение бокового выноса ног при
стабилизации по углу крена, либо переднего выноса ног при стабилизации по углу тангажа).
Полученные при этом законы движения используются в качестве номинальных в алгоритмах
стабилизации движения аппарата по управляемым координатам.
УРАВНЕНИЯ ДВИЖЕНИЯ ША В РЕЖИМЕ ПРЫЖКОВ
Математическая модель движения аппарата в фазе опоры
Рассматриваетсяо движение, состоящее из опорной фазы, в течение которой все ноги аппарата
соприкасаются с поверхностью, и безопорной фазы полета.
В опорной фазе движение ША описывается уравнениями (1)-(3).
В фазе полета ША должен двигаться так, чтобы удовлетворять краевым условиям:
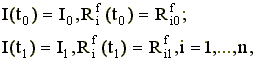 , (7)
, (7)
где
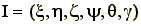 - совокупность управляемых координат корпуса,
- совокупность управляемых координат корпуса,
 - векторы, характеризующие положения стоп ног в
абсолютном пространстве,
- векторы, характеризующие положения стоп ног в
абсолютном пространстве,
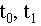 - моменты начала и окончания прыжка соответственно.
- моменты начала и окончания прыжка соответственно.
Программное движение ША в фазе опоры
Задачей управления ША в опорной фазе является создание начальных условий, позволяющих
обеспечить безопорную фазу движения с требуемой дальностью, высотой и направлением полета.
Поза аппарата в моменты его отделения от опорной поверхности играет существенную роль.
Ее обеспечение является одним из элементов этапа подготовки к выполнению прыжка. Процедура
формирования начальной позы перед прыжком следующая.
Опорный контур в проекции на горизонтальную плоскость
 зададим прямоугольником,
длина которого равна расстоянию между точками подвеса передних и задних ног. С проекцией
опорного контура на плоскость
зададим прямоугольником,
длина которого равна расстоянию между точками подвеса передних и задних ног. С проекцией
опорного контура на плоскость  свяжем систему координат
свяжем систему координат
 , где
, где  -
центр соответствующего опорного контура, а оси координат перпендикулярны его сторонам
(см. рис. 2).
-
центр соответствующего опорного контура, а оси координат перпендикулярны его сторонам
(см. рис. 2).
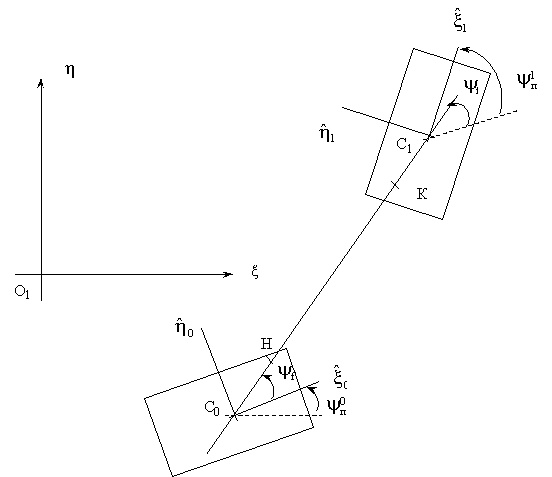
Рисунок 2 - Формирование позы перед прыжком
Потребуем, чтобы в процессе подготовительного этапа проекция центра масс корпуса на
горизонтальную плоскость не отклонялась от продольной оси
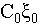 на расстояние, большее, чем d.
Назовем дальностью прыжка L расстояние между центрами исходного и следующих опорных контуров
в проекции на горизонтальную плоскость (отрезок
на расстояние, большее, чем d.
Назовем дальностью прыжка L расстояние между центрами исходного и следующих опорных контуров
в проекции на горизонтальную плоскость (отрезок 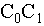 ).
Азимут
).
Азимут 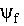 характеризует направление
движения в предстоящей фазе полета, азимут
характеризует направление
движения в предстоящей фазе полета, азимут 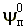 характеризует ориентацию исходного опорного
контура, а
характеризует ориентацию исходного опорного
контура, а 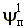 - опорного контура в момент приземления. Абсолютные координаты стоп в момент
приземления могут быть определены по известным координатам центра опорного контура, его
ориентации, размерам и прямоугольной форме проекции на горизонтальную плоскость с привлечением
информации о рельефе.
- опорного контура в момент приземления. Абсолютные координаты стоп в момент
приземления могут быть определены по известным координатам центра опорного контура, его
ориентации, размерам и прямоугольной форме проекции на горизонтальную плоскость с привлечением
информации о рельефе.
Математическая модель движения ША в фазе полета
Будем считать, что на аппарат в фазе полета действует только сила тяжести, параллельная
абсолютной оси. Центр масс аппарата движется в соответствии с законом
 ,(8)
,(8)
где  - абсолютный радиус-вектор центра масс,
- абсолютный радиус-вектор центра масс,
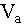 - его скорость, g - вектор ускорения силы тяжести.
Индекс 0 означает, что величины отнесены к моменту
- его скорость, g - вектор ускорения силы тяжести.
Индекс 0 означает, что величины отнесены к моменту  .
.
Построение программного движения аппарата в фазе полета
Краевые условия (7) позволяют рассчитать абсолютное положение центра масс аппарата в начальный
и конечный моменты времени. Из закона движения (8) можно найти затем продолжительность
безопорной фазы и начальную скорость центра масс. В самом деле, пусть тангенс угла наклона искомой н
ачальной скорости к горизонтальной плоскости
 равен
равен
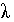 , тогда
, тогда
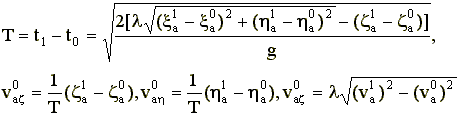 . (9)
. (9)
Формула имеет смысл только для достаточно больших значений 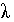 .
На основе закона (8) формируются траектории переноса ног. Краевые условия (7) позволяют
рассчитать шарнирные углы в начальный и конечный моменты времени
.
На основе закона (8) формируются траектории переноса ног. Краевые условия (7) позволяют
рассчитать шарнирные углы в начальный и конечный моменты времени
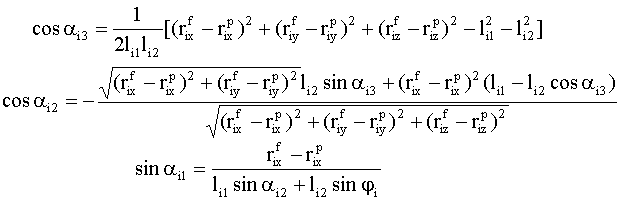 , (10)
, (10)
где  - угол поворота в j-того звена i-той ноги,
- угол поворота в j-того звена i-той ноги,
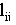 - длина j-того звена i-той ноги.
Начальную и конечную скорости шарнирных углов целесообразно назначать, исходя из требования
мягкости отделения ног от опорной поверхности и их постановки после окончания прыжка.
Это требование запишем в виде:
- длина j-того звена i-той ноги.
Начальную и конечную скорости шарнирных углов целесообразно назначать, исходя из требования
мягкости отделения ног от опорной поверхности и их постановки после окончания прыжка.
Это требование запишем в виде:
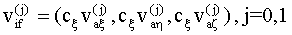 , (11)
, (11)
где  - достаточно малые заданные постоянные.
- достаточно малые заданные постоянные.
Стабилизация движения аппарата в фазе полета
Возмущения, действующие в фазе подготовки к прыжку, вызывают отклонение момента времени отделения
от опорной поверхности по сравнению с запланированным, а также начальные ошибки координат и
скоростей аппарата. В результате меняется дальность прыжка и возникает дополнительное вращение
корпуса во время полета. Появляется необходимость в корректировке характеристик предстоящего
прыжка по измерениям, предшествующим его началу. К таким характеристикам отнесем
продолжительность и дальность безопорной фазы полета, значение вектора кинетического момента
аппарата относительно центра масс, параметры закона движения ног при переносе.
Движение центра масс в фазе полета неуправляемо. Он движется по баллистической траектории в
соответствии с законом (8).Целью стабилизации является обеспечение заданного программного
положения аппарата в момент приземления с учетом сдвига, вызванного ошибкой положения центра
масс в этот момент.
Можно использовать достаточно простой метод управления ориентацией корпуса аппарата в
безопорной фазе. В номинальном движении ноги аппарата в процессе полета должны переноситься
из "заднего" положения, остающегося после отделения от опорной поверхности, в "переднее"
положение, необходимое для обеспечения устойчивого движения в фазе приземления. Указанный
перенос ног и требование горизонтального положения корпуса в момент приземления приводят к
необходимости сообщать аппарату при прыжке начальную угловую скорость вокруг поперечной оси.
Изменяя в полете положение ног и момент инерции аппарата можно варьировать величину угловой
скорости и влиять на угловое положение аппарата в момент приземления.
Экспериментальные исследования особопроходимых походок путем
моделирования их на ПЭВМ
Моделирование специальных походок в режиме бега
Исследован бег парными походками: иноходь, галоп, рысь. Для этих походок получены графические
зависимости управляемых координат от времени при ненулевых начальных условиях. Полученные
зависимости приведены на рис.3-10.
Иноходь

Рисунок 3 - Зависимость угла рыскания от времени

Рисунок 4 - Зависимость угла тангажа от времени
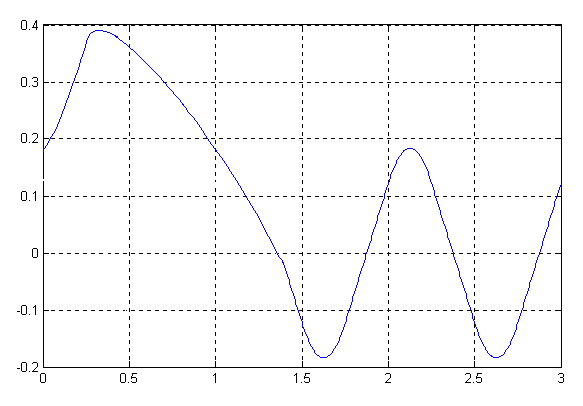
Рисунок 5 - Зависимость угла крена от времени
Рысь

Рисунок 6 - Зависимость угла рыскания от времени
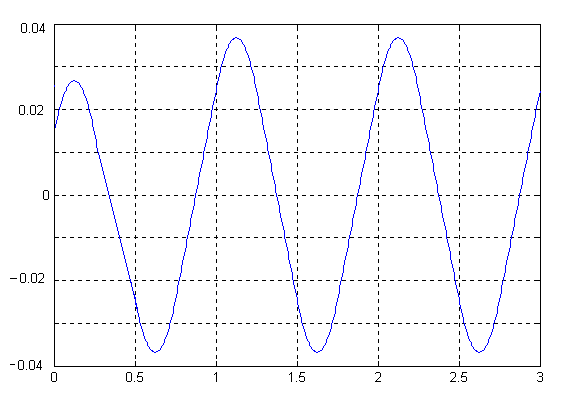
Рисунок 7 - Зависимость угла тангажа от времени
Галоп

Рисунок 8 - Зависимость угла рыскания от времени

Рисунок 9 - Зависимость угла тангажа от времени
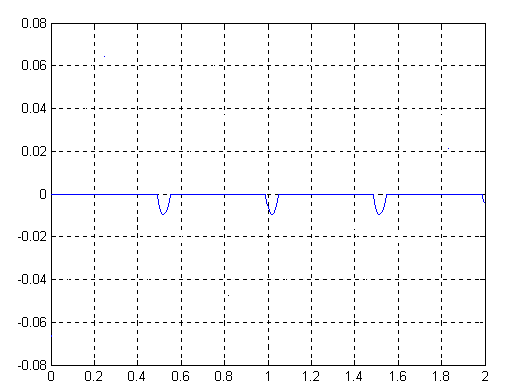
Рисунок 10 - Зависимость угла крена от времени
Моделирование специальных походок в режиме прыжков
На стадии разработки
Перечень ссылок
1. Охоцимский Д.Е., Платонов А.К., Лапшин В.В. Исследование энергетики движения шестиногого шагающего аппарата. Препринт ИППМ АН СССР - М.: 1981, №96 - 29 с.
2. Лапшин В.В. Управление движением четырехногого шагающего аппарата. Препринт ИППМ АН СССР - М.: 1984, №83 - 27 с.
3. Охоцимский Д.Е., Голубев Ю.Ф., Алексеева Л.А.Управление динамической моделью шагающего аппарата. Препринт ИППМ АН СССР - М.: 1974, №20 - 56с.
4. Охоцимский Д.Е., Голубев Ю.Ф. Механика и управление движением автоматического шагающего аппарата. - М.: Наука, 1984. - 312 с.
5. Лапшин В.В. Алгоритм построения программного движения прыгающего аппарата для фазы полета. Препринт ИППМ АН СССР - М.: 1979, №26 - 50с.
6. Лапшин В.В. Опорная фаза движения многоногого прыгающего аппарата. Препринт ИППМ АН СССР - М.: 1978, №126 - 70 с.
АПРОБАЦИЯ РЕЗУЛЬТАТОВ
К настоящему времени участвовала в III Международной научно-технической
конференции, котораz проводились в Донецком национальном техническом университете на кафедре ГЭА.
Доклад на тему "Моделирование динамики бега четырехногого шагающего аппарата" был отмечен
дипломом. На ту же тему опубликована статья в сборнике трудов конференции.
Статья «Разработка алгоритмов управления шестиногим шагающим аппаратом при
движении прыжками» была опубликована в сборнике приуроченном ко Дню науки факультета КИТА.
ЗАКЛЮЧЕНИЕ И ПЕРСПЕКТИВЫ ИССЛЕДОВАНИЯ
В ходе выполнения работы
1. Исследовано пространственное движение четырехногого аппарата с невесомыми ногами,
перемещающегося парными походками (рысь, иноходь и галоп).
2. Получена математическая модель динамики движения в режиме бега и прыжков. Приведены
аналитические выражения для фазы полета и опоры.
3. Решены задачи построения программного движения и стабилизации движения аппарата.
4. Проведены экспериментальные исследования походок в режиме бега на ПЭВМ при помощи пакета
прикладных программ MATLAB 6.0 и Simulink 4.0. Получены графические зависимости изменения управляемых координат
центра масс, доказывающие работоспособность синтезированных алгоритмов стабилизации движения
при наличии различного рода возмущений.
Исследование движения ША в режиме бега были проведены для четырехногого аппарата, однако
полученные алгоритмы можно будет применить и для шестиногого аппарата. При этом пара средних ног
используется как манипуляторы и не принимает участи в организации движения.
новизна работы заключается в том, что моделирование проводилось при помощи современного
программного обеспечения, что позволило значительно сократить время выполнения программ и облегцить
работу над преобразованием алгоритмов в программы, а также позволит легко их модернизировать при необходимости.
В дальнейшем будет проведено экспериментальное исследование движения аппарата в режиме прыжков.
<Вверх>
 (плоскость
(плоскость
 - горизонтальна) определяется
координатами центра масс корпуса
- горизонтальна) определяется
координатами центра масс корпуса
 и углами
и углами
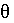 - рыскания,
- рыскания,
 - тангажа,
- тангажа,
 - крена.
ША движется осью Оу вперед. Ось Оz является конструктивной вертикалью корпуса.
- крена.
ША движется осью Оу вперед. Ось Оz является конструктивной вертикалью корпуса.

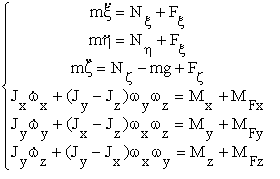 , (1)
, (1)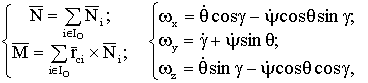 , (2)
, (2)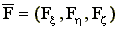 - возмущающие силы;
- возмущающие силы;
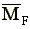 - момент возмущающих сил относительно
центра масс корпуса;
- момент возмущающих сил относительно
центра масс корпуса;
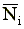 - реакции в точках опоры ног;
- реакции в точках опоры ног;
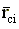 - радиус-вектор стопы i-той ноги
в системе координат Oxyz;
- радиус-вектор стопы i-той ноги
в системе координат Oxyz;
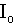 - множество индексов опорных ног в
текущий момент времени;
- множество индексов опорных ног в
текущий момент времени;
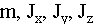 - масса и главные моменты инерции корпуса.
Величина возмущающих сил
- масса и главные моменты инерции корпуса.
Величина возмущающих сил
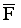 и их момента относительно центра масс
и их момента относительно центра масс 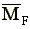 не
известна системе управления движением аппарата. При решении задач построения программного
движения и стабилизации движения аппарата
не
известна системе управления движением аппарата. При решении задач построения программного
движения и стабилизации движения аппарата
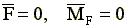 . (3)
. (3) ) следует фаза полета.
Одну опорную фазу движения и следующую за ней фазу полета будем называть шагом.
Продолжительность фазы полета
) следует фаза полета.
Одну опорную фазу движения и следующую за ней фазу полета будем называть шагом.
Продолжительность фазы полета
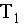 не меняется от шага к шагу. Программное движение обеспечивает равномерность нагрузки в
опорной фазе на обе опорные ноги и строится так, что в проекции на горизонтальную
поверхность центр масс аппарата движется равномерно и прямолинейно [2]
не меняется от шага к шагу. Программное движение обеспечивает равномерность нагрузки в
опорной фазе на обе опорные ноги и строится так, что в проекции на горизонтальную
поверхность центр масс аппарата движется равномерно и прямолинейно [2]
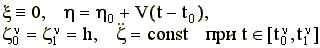 , (4)
, (4) - момент начала опорной фазы
- момент начала опорной фазы
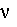 -го шага,
-го шага,
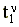 - момент начала фазы полета,
- момент начала фазы полета,
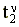 - момент окончания
- момент окончания
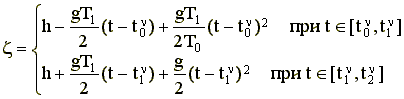 . (5)
. (5)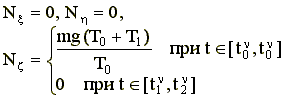 . (6)
. (6)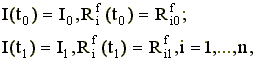 , (7)
, (7)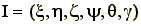 - совокупность управляемых координат корпуса,
- совокупность управляемых координат корпуса,
 - векторы, характеризующие положения стоп ног в
абсолютном пространстве,
- векторы, характеризующие положения стоп ног в
абсолютном пространстве,
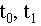 - моменты начала и окончания прыжка соответственно.
- моменты начала и окончания прыжка соответственно.
 , где
, где  -
центр соответствующего опорного контура, а оси координат перпендикулярны его сторонам
(см. рис. 2).
-
центр соответствующего опорного контура, а оси координат перпендикулярны его сторонам
(см. рис. 2).

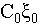 на расстояние, большее, чем d.
Назовем дальностью прыжка L расстояние между центрами исходного и следующих опорных контуров
в проекции на горизонтальную плоскость (отрезок
на расстояние, большее, чем d.
Назовем дальностью прыжка L расстояние между центрами исходного и следующих опорных контуров
в проекции на горизонтальную плоскость (отрезок 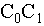 ).
Азимут
).
Азимут 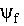 характеризует направление
движения в предстоящей фазе полета, азимут
характеризует направление
движения в предстоящей фазе полета, азимут 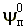 характеризует ориентацию исходного опорного
контура, а
характеризует ориентацию исходного опорного
контура, а 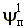 - опорного контура в момент приземления. Абсолютные координаты стоп в момент
приземления могут быть определены по известным координатам центра опорного контура, его
ориентации, размерам и прямоугольной форме проекции на горизонтальную плоскость с привлечением
информации о рельефе.
- опорного контура в момент приземления. Абсолютные координаты стоп в момент
приземления могут быть определены по известным координатам центра опорного контура, его
ориентации, размерам и прямоугольной форме проекции на горизонтальную плоскость с привлечением
информации о рельефе.
 ,(8)
,(8) - абсолютный радиус-вектор центра масс,
- абсолютный радиус-вектор центра масс,
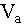 - его скорость, g - вектор ускорения силы тяжести.
Индекс 0 означает, что величины отнесены к моменту
- его скорость, g - вектор ускорения силы тяжести.
Индекс 0 означает, что величины отнесены к моменту  .
.
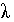 , тогда
, тогда
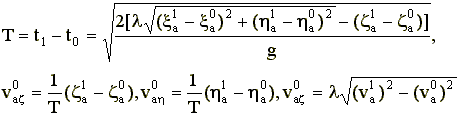 . (9)
. (9)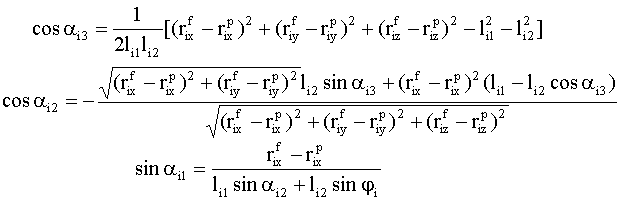 , (10)
, (10) - угол поворота в j-того звена i-той ноги,
- угол поворота в j-того звена i-той ноги,
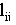 - длина j-того звена i-той ноги.
Начальную и конечную скорости шарнирных углов целесообразно назначать, исходя из требования
мягкости отделения ног от опорной поверхности и их постановки после окончания прыжка.
Это требование запишем в виде:
- длина j-того звена i-той ноги.
Начальную и конечную скорости шарнирных углов целесообразно назначать, исходя из требования
мягкости отделения ног от опорной поверхности и их постановки после окончания прыжка.
Это требование запишем в виде: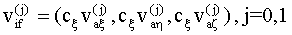 , (11)
, (11) - достаточно малые заданные постоянные.
- достаточно малые заданные постоянные.







