Иванова Ольга Юрьевна E-mail: olgivanova@ukr.net специальность: "Системы управления автоматикой" Тема магистерской работы: "Математическое моделирование динамики движения шестиногого шагающего аппарата" Научный руководитель: доц., к.т.н. Рафиков Г. Ш.

Развитие робототехники было связано с необходимостью исследования территории с "агрессивной" средой. Необходимость создания наземных транспортных средств высокой проходимостью заставила обратиться к созданию машин, перемещающихся с помощью конечностей. Предполагается, что такие положительные качества шагающего аппарата, как высокая адаптация к неровностям опорной поверхности, принципиально более высокая маневренность, допускающая перемещение машины в произвольном направлении и повороты на месте, опорная проходимость по грунтам с низкой несущей способностью, возможность комфортабельного движения позволяет занять одно из ведущих мест в робототехнике. Однако, данные аппараты имеют довольно сложную систему управления движением. Исследование динамики движения шестиногого аппарата составляет большую долю в построении системы управления движением.

Разработка шагающего способа перемещения искусственных объектов насчитывает около 150 лет и знаний за этот период накопленно достаточно много. Однако полностью решить все вопросы решить так и не удалось. В данной работе для гиппотетического аппарата заданного линейными размерами и масс-инерционными характеристиками, характеристиками двигетелей и редукторов описана кинематика его движения. Построена методика решения обратной задачи динамики для шгающего аппарата с двигателями постоянного тока, позволяющая расчитать динамические и энергетические характеристики движения аппарата и двигателей в шарнирах ног, соответствующие заданной кинематике движения аппарата. В модели учитывается динамика электроприводов в шарнирах ног, трение в двигателях и редукторах. Предложен способ решения задачи распределения уссилий итерационным методом. Исследована зависимость энергозатрат аппарата от кинематических параметров аппарата. Решена задача параметрической оптимизации киненматики движения аппарата с точки зрения минимизации средней мощности, потребляемой двигателями в шарнирах ног. Получены характеристики движения шагающего аппарата при преодолении одиночных препятствий типа "щель" и "уступ".

1. Характеристика шестиногого шагающего аппарата
   
   На рисунке 1 изображен шестиногий шагающий аппарат. Система координат Oxyz жестко связана с корпусом аппарата. Ось Ox направлена вперед по движению аппарата. Положение корпуса относительно осей абсолютной системы координат определяется координатами точки O корпуса аппарата и тремя углами (тангаж, крен, рысканье). Каждая нога аппарата состоит из трех звеньев, которые будем называть соответственно платформой, бедром, голенью. Звенья ноги лежат в одной плоскости, которая параллельна оси Oz. Положение ноги относительно корпуса определяется углами:α₁ - угол в шарнире платформы, α₂ - угол в шарнире бедра, α₃ - угол в коленном шарнире [1].
   
   Рисунок 1 - Шестиногий шагающий аппарат
   
   
   Виды походок движения шестиногого шагающего аппарата
   

   По мере накопления опыта проектирование шагающих машин становилось ясно, что при построении реальной шагающей машины ее походка является одним из решающих конструктивных фактором. И действительно, походка является определяющим фактором, так как она связывает геометрию машины с проходимостью. Кроме того, походка оказывает сильное влияние на управляющий алгоритм шагающей машины, поскольку она сама является производной системы управления. До некоторой степени она оказывает влияние и на энергетическую эффективность машины. Это станет более ясно видно из последующего обсуждения.

   Походка искусственной локомоционнной системы представляет собой взаимосогласованное движение ног и корпуса, в; результате которого система перемещается из одной точки пространства и другую. Первые исследования походок предпринимались зоологами, которые с помощью схем, диаграмм и фотографии описывали походки, наблюдаемые при движении животных. Со временем анализировать походки начали и некоторые инженеры, в основном энтузиасты создания шагающих машин. Однако для систематического изучения походок требовалось точно определить множество параметров, большинство которых было определено при анализе походок в работах, базировавшихся в основном на численных методах и нелинейном программировании.

   Основными периодическими походками являются волновая, полуцикловая равнофазная, след в след. На рисунках ниже приведены диаграммы основных походок.

   
   
   Рисунок 2 - Диаграмма волновой походки
   

   Волновые походки относятся к числу наиболее устойчивых регулярных походок; их можно наблюдать и в природе при ходьбе млекопитающих и насекомых по ровной поверхности. Это и дало основание некоторым исследователям предлагать эти походки в качестве основных типов походок для шагающих машин. При равнофазной походке события подъема и опускания ног равномерно распределены по циклу ходьбы. Если во время этих событий из системы забирается сколько-нибудь значительная мощность, то равнофазная походка идеально подходит для ограничения пика потребной мощности.

   
   

   
   Рисунок 3 - Диаграмма походки типа «след в след»
   

   
   В походке типа «след в след» обе передние ноги ставятся на землю независимо в два разных предварительно выбранных места. Ступни всех остальных ног ставятся или непосредственно в след, или вблизи следа, оставленного передней ногой. Таким образом, необходимость выбора мест постановки ноги и соответствующая регулировка положения ступней сводятся к минимуму. Более того, походка «след в след» обеспечивает больший допуск на выбор положений ступней и, следовательно, обход более обширных запрещенных областей. Преимуществом периодической походки «след в след» является плавность движения корпуса; кроме того, с се помощью можно сохранять более высокую скорость на неровной местности. Возможно, именно по этой причине рисунок ходьбы многих животных строится на принципах периодической походки «след в след»[2].
   
   
   Характеристики типов опорных поверхностей
   
   
   Ниже приведена классификация типов опорных поверхностей [3].
   
   Таблица 1 - Типы опорных поверхностей и их характеристика по несущей способности
   

   Класс опорной поверхности	Тип поверхности и грунтового массива	Механическая модель и вид разрушения
   1. Жесткие опорные поверхности	Сплошной грунтовой массив (грунты с первичными жесткими связями)	Твердое тело; сопротивление за счет прочности связей; разрушений нет
   	Твердый грунт над горными выработками, плывунами без прочного подстилающего основания	Твердое тело; хрупкое разрушение сплошности пласта с раскалыванием на части разной величины
   	Корка смерзшегося грунта над слабыми основаниями
   2. Деформируемые опорные поверхности	Несвязные скелетные грунты и породы (насыпные и естественно-залегающие); рыхлый сыпучий снег	Сыпучее тело. Разрушения: а) в массиве - колееобразование; б) на откосах и в насыпях - обрушение грунта
   	Связные деформируемые грунты в виде глубокого массива; снеговой покров земли	Пористое тело; трехфазная система или грунтовая масса; разрушение в виде колееобразования
   	Связные деформируемые грунты на твердом, близко расположенном массиве
   3. Слабые опорные поверхности	Слои переувлажненных грунтов в текучем и близком к текучему состояниях, лежащие на твердом основании	Вязкая жидкость на твердом основании
   	Водонасыщенные грунтовые образования значительной глубины (болота, спущенные пруды и др.)	Вязкая и вязко-пластичная жидкость с низкой несущей способностью, без твердого основания
   	Неминеральные почвы органического происхождения (торфяники) в массиве	Малопрочное упругое тело; разрушения в виде колееобразования
   	Сплошные растительные образования (травяной покров) на болотах без прочного основания	Малопрочное хрупкое тело; разрушения в виде разрывов сплошности верхнего слоя; возможно колееобразование
   	Снеговой покров с твердым наростом над малопрочным массивом снега	Хрупкое тело; разрушение в виде провалов в местах нагружения

   
   Таблица 2 - Характеристики грунтовых поверхностей по сопротивлению деформированию под нормальной нагрузкой от опор ШМ

   Тип грунтового массива	Вид грунтовой поверхности или массива	Модель реологического состояния, схема и возможные законы деформирования
   2. Деформируемые опорные поверхности
   Несвязные скелетные грунты и породы (без жестких связей)	Сыпучие пески в уплотненном, разрыхленном или увлажненном состоянии в массиве	Упругое тело или нерелаксирующее упруговязкое тело. Линейно-деформируемое основание или степенная функция деформирования; безопасные нагрузки
   	Насыпные пески, галька, щебень, каменные материалы на уплотненном основании; сухая пыль
   	Пески и породы в насыпях и у краев выемок
   Тип грунтового массива	Вид грунтовой поверхности или массива	Модель реологического состояния, схема и возможные законы деформирования определяются по предельному состоянию равновесия грунта
   Связные грунты и минеральные почвы в массиве близлежащего твердого основания	Молекулярно-связываемые грунты в твердопластичном состоянии при относительной влажности Wот=0,3-0,4	Упруговязкое тело
   	Молекулярно-связываемые грунты в вязкопластичном состоянии при Wот=0,5-0,6	Упруговязкопластичное тело или степенная функция деформирования
   	Почвы и целина с травяным покровом и развитой корневой системой в твердо- или вязкопластичном состоянии
   Связные грунты и почвы на близко расположенном основании	Насыпные молекулярносвязываемые грунты на твердом, хорошо фильтруемом основание при Wот <0,7	Упруговязкое тело; упруговязкопластичное тело
   	Размокшие грунтовые дороги с пластичным верхним слоем до 30-50 см
   	Вспаханная почва при Wот=0,6-0,75
   	Сельскохозяйственные поля без развитой корневой системы при Wот <= 0,7-0,8 (после уборки урожая)
   	Жнивье зерновых культур; травяные залежи; луга неполивные (со слабым корневым или травяным покровом)
   	Поймы рек и осушенные водоемы с илистыми структурными отложениями на плотном основании
   3. Слабые опорные поверхности
   Водонасыщенные грунтовые образования на твердом основании	Оттаивающие мерзлые связные грунты	В текучем слое - почти полностью отсутствует сопротивление: текучая жидкость (схема Паскаля);
   Сельскохозяйственные поля, пашня, целина, лесные проезды при интенсивном увлажнении и плохом водоотводе (Wот >0,8)
   	Переувлажненные грунтовые дороги на глубину до 30-50 см и более при слабом водоотводе с поверхности и слабофильтруемом основании в вязкой жидкости появляется сопротивление за счет деформируемости связей: вязкая жидкость (схема Ньютона) и релаксирующая жидкость (схема Максвелла)
   	Заливные луга, поймы рек, участки поливного земледелия
   Водонасыщенные грунтовые образования без жесткого близлежащего основания	Грунтовые суспензии; ил в водоемах; плывуны песчаного и илового состава	Вязкая жидкость; релаксирующая упруговязкая жидкость
   	Некоторые виды болот
   Неминеральные почвы и грунты почвенно-растительного и органического происхождения	Увлажненные и водонасыщенные торфы разного состава	Упругое малопрочное тело или упругопластичное тело (схема Сен-Венана); сопротивление за счет прочности связей при отсутствии внутреннего трения
   	Лугово-болотные и болотные почвы, торф над слоем сапропеля или водоема значительной глубины
   	Осушенная торфяная залежь различного органического состава	Упругопластичное малопрочное тело; сопротивление за счет внутренних связей при внутреннем трении

   
   Таблица 3 - Характеристика опорных поверхностей движения по сцеплению с ними опор ШМ

   Тип опорной поверхности	Вид и состояние поверхности	Механическая модель и вид трения-сцепления
   	1. Жесткие опорные поверхности
   Твердые грунты, породы	Сухое чистое покрытие	Полусухое трение материала опор о поверхность покрытия
   	Влажная и мокрая поверхность твердого покрытия; травяной покров грунта; наносы мокрого грунта и грязи на твердом покрытии покрытии	Полужидкостное и жидкостное трение
   	Обледенелое и заснеженное состояние поверхности; лед и уплотненный сухой чистый снег при температуре воздуха < -20С	Полусухое трение
   	Тающий лед и снег при температуре воздуха от минус 2 до плюс 50С	Жидкостное трение
   	Слой сыпучего неуплотненного снега на обледенелом или заснеженном покрытии при температуре воздуха от минус 2 до плюс 50С	Полужидкостное трение материала опор о лед и внутреннее трение в снегу
   	Оттаивающий мерзлый связный грунт	Жидкостное и вязкое трение
   	2. Деформируемые опорные поверхности
   Несвязные скелетные грунты	Массив несвязного грунта (пески) в плотном состоянии	Полусухое трение опор о грунт
   	Сыпучие разрыхленные и насыпные пески в массиве и на твердом основании, сухие и увлажненные	Сцепление за счет внутреннего трения в грунте
   Связные грунты и почвы	Грунты в твердопластичном состоянии Wот=0,3 - 0,5	Сопротивление грунта сдвигу определяется внутренним трением и сцеплением
   Грунты в вязкопластичном состоянии Wот=0,5 - 0,7
   Связные грунты и почвы	Грунты с дерновым покровом или корневой системой в сухом или увлажненном состояниях	Сопротивление грунта сдвигу определяется внутренним трением и сцеплением
   Тип опорной поверхности	Вид и состояние поверхности	Механическая модель и вид трения-сцепления
   3. Слабые грунтовые образования
   Водонасыщенные грунтовые образования без близлежащего жесткого основания	Связные грунты в вязком состоянии при 0,7<Wот<0,95	Вязкое трение: в текучем состоянии грунты имеют ничтожное сцепление и незначительное внутреннее трение
   		Связные и сыпучие грунты, залитые с поверхности водой (поймы, берега рек и озер, спущенные пруды с илом и др.)
   Водонасыщенные грунтовые образования без близлежащего жесткого основания	Грунты в вязкотекучем состоянии (болота)	На вязком грунте сцепление обусловлено жидкостным или вязким трением
   Неминеральные почвы и грунты органического и почвенно-растительного происхождения	Осушенная торфяная залежь	Сцепление обусловлено внутренним трением и сцеплением
   Увлажненные торфяники; лугово-болотные почвы, перенасыщенные водой	Полужидкостное трение по поверхности контакта и сопротивление срезу почвы в массиве

   
   Таблица 4 - Виды неровностей и препятствий на опорных поверхностях перемещения ШМ

   Класс опорной поверхности	Вид поверхностей	Типичные неровности, препятствия и их характеристика
   Жесткие опорные поверхности	Дороги с неровным покрытием, ледовым покровом и укатанным снегом	Волнистость, выбоины, неровный лед, снег. Неровности описываются статистическими характеристиками случайного микропрофиля дороги.
   	Городские дороги, строительные площадки	Узкие улицы и проезды
   Класс опорной поверхности	Вид поверхностей	Типичные неровности, препятствия их характеристика
   	Естественные проезды на местности в лесах и на мелколесье, при лесоразработках	Древесно-кустарниковая растительность, деревья, пни, срезанные деревья, кустарник
   	Сухие грунтовые дороги	Колейность, выбоины, волнистость, ямы со скоплениями пыли
   	Специальные инженерные сооружения	Вертикальные стенки, окопы, эскарпы, рвы, канавы
   	Каменная порода в карьерах и на местности	Валуны, крупная галька, щебень
   	Стесненные проезды в горах	Глубокие расщелины, мелкие горные реки, намывы камней и песка
   2.Деформируемые опорные поверхности	Пахота неборонованная и боронованная в сухом состоянии	Твердые структурные образования из грунта; борозды
   	Сельскохозяйственные поля после уборки урожая в сухом состоянии	Неровности случайного микропрофиля, описываемые статистическими характеристиками
   	Плотные и сыпучие пески в естественном залегании, сухие	Мелкие и средние барханы, волнистость поверхности, холмы
   	Насыпной грунт и каменные материалы (галька, щебень) на строительных площадках, в отвалах карьеров	Насыпи и россыпи в состоянии неустойчивого равновесия (возможны обрушения)
   	Увлажненные грунтовые дороги	Глубокие колеи, выбоины, волнистость; ямы, залитые водой
   3. Слабые грунтовые образования	Поймы, осушенная залежь, спущенные пруды, берега водохранилищ	Крутые откосы берегов, канавы, рвы, запруды, обрушенные
   Класс опорной поверхности	Вид поверхностей	Типичные неровности, препятствия и их характеристика деревья
   	Торфяники, лугово-болотные почвы, плывуны	Кустарник, кочковатая растительность, мелколесье

   
   
   Разработка блока формирования походки шагающего аппарата
   
   
   Движение каждой конечности шагающего аппарата представляет собой чередование фаз опоры и переноса. Под фазой опоры будем понимать движение конечности с момента начала вертикального опускания ее конца на опорную поверхность до момента отрыва от нее.
   Введем функции так, что , если i-я нога в момент времени t находится в фазе опоры, и = 1, если 1-я нога находится в момент времени t в фазе переноса.
   Введем кусочно-постоянную вектор-функцию
   
   Столбец назовем состоянием аппарата в момент времени c помощью введенной вектор-функции любую походку аппарата можно описать упорядоченной во времени последовательностью столбцов (матрицей), состоящих из 0 и 1.
   В дальнейшем под походкой будем понимать упорядоченную последовательность состояний аппарата. Назовем походку периодической, если последовательность периодическая. Очевидно, что для описания периодической походки можно ограничиться матрицей состояний с числом столбцов, равным минимальному периоду исходной последовательности, а для описания перехода с одной периодической походки на другую — указать конечную матрицу (последовательность) состояний данного перехода. Назовем эти матрицы задающими.
   
   Последовательность дискретных состояний заданной походки реализуется в движении аппарата непрерывными кривыми, описывающими изменение углов в суставах конечностей аппарата. Формировать эти кривые в процессе движения аппарата удобно с помощью генераторов шаговых циклов [4], используя для управления их работой вектор-функцию . Для формирования вектор-функции удобно до начала движения записать в долговременную память системы управления последовательность , отвечающую заданной походке и в процессе движения обновлять значения, считывая из памяти системы управления очередной столбец — состояние ,. в соответствующий момент времени. Кроме последовательности состояний, необходимо задавать еще моменты перехода из одного состояния в другое.
   Шесть идентичных генераторов шаговых циклов (по числу ног) формируют прообразы траекторий движения концов ног аппарата на плоскости вспомогательных декартовых координат как решение системы дифференциальных уравнений вида
   
   
   ,
   где К — вектор управлений, — вектор параметров. Характерный вид решения уравнений на плоскости приведен на рисунке, где 1 — фаза опоры; 2 — фаза переноса,участок отрыва; 3—фаза переноса, участок подъема; 4—фаза переноса; 5—фаза переноса, участок опускания; 6—фаза опоры, участок наступания.
   Генераторы шаговых циклов функционируют так, что для всех ног, находящихся в фазе опоры (1,6), одинаковы.
   
   Рисунок 4 - Характерный вид траектории шагового цикла
   
   Заметим, что если переход конечности аппарата на фазу переноса возможен в любой момент в течение фазы опоры (переход с участка 1 на участок 2 траектории шагового цикла), то переход в фазу опоры возможен лишь по завершении всех этапов фазы переноса (отрыв, подъем, перенос, опускание). Поэтому целесообразно организовать управление работой генераторов шаговых циклов так, чтобы переход с фазы опоры па фазу переноса происходил по внешнему (по отношению к генератору) управляющему сигналу, а переход с фазы переноса на фазу опоры производился «автоматически» за счет надлежащего выбора параметров генератора. При этом выбор параметров генератора необходимо производить так, чтобы конец ноги занял предписанное положение к предполагаемому моменту времени начала фазы опоры.
   
   При такой организации смены фаз движения конечностей аппарата походка может задаваться под последовательностью исходной последовательности состояний, в которой сохранены лишь столбцы, отвечающие переходу какой-либо ноги в фазу переноса.
   Будем рассматривать только периодические походки. Как отмечалось ранее, периодические походки можно описать с помощью задающих матриц. В задающих матрицах периодических походок и переходов с одной и них на другую можно выделить столбцы отвечающие переходу какой-либо ноги в фазу переноса. Матрицы, составленные из выделенных столбцов (с сохранением упорядоченности), назовем базовыми матрицами периодических походок и переходов с одной из них на другую. Число столбцов в базовой матрице периодической походки назовем параметром походки. Приведем для примера базовые матрицы походок «трешки», «галоп» и перехода «трешки—галоп» соответственно:
   .
   Введем понятие обобщенного времени следующим образом:
   
   — скорость движения изображающей точки по траектории шагового цикла в фазе опоры , — постоянная, имеющая размерность скорости. В обобщенном времени скорость движения изображающей точки на фазе опоры постоянна и равна а.
   
   Рассмотрим теперь периодические походки, в которых все шесть генераторов шаговых циклов формируют идентичные траектории, отличающиеся лишь фазовыми сдвигами с постоянными в обобщенномом времени длительностями: — опоры. -переноса, - цикла.
   Ограничимся походкам, при которых до и после фазы переноса каждой ноги имеется фаза переноса каждой ноги имеется фаза совместной опоры на все ноги длительностью . Будем называть такие походки регулярными.
   Можно показать, что существует следующее соотношение:
   
   Введем еще время такта
   Целесообразность рассмотрения регулярных походок определяется простотой их реализации: в обобщенном времени через интервалы происходит переход в фазу переноса конечностей, номера которых определяются соответствующим столбцом базовой матрицы.
   При заданных однозначно определяются обобщенное время фазы переноса , обобщенное время фазы опоры и длины шага
   Реальное время фазы переноса и фазы опоры зависит от
   Регулярная походка задается следующими параметрами: базовой матрицей и соответствующим , а также параметрами и
   При реализации регулярных походок с помощью управляемых генераторов шаговых циклов удобно для управления моментами переходов соответствующих конечностей аппарата в фазу переноса использовать вместо кусочно-постоянную вектор-функцию .
   Интервалы постоянства в обобщенном времени равны , а значения совпадают с соответствующими столбцами базовой матрицы.
   
   4.1 Функциональная схема блока формирования походки и принцип ее работы
   Функциональная схема блока формирования походок, включенного в систему управления шагающего аппарата изображена на рисунке. Собственно блок формирования походки (БФП) выделен штриховой линией. Он содержит следующие основные модули.
   
   
   БФП —блок формирования походки, 1 —модуль генераторов шаговых циклов, 2— модуль формирования последовательности движения конечностей, 3— генератор ритма, 4 — модуль параметров; БЛП — блок линейного преобразования; БМ— блок маневрирования; БПК—блок преобразователей координат; БУСС—блок усилителей следящей системы.
   
   Рисунок 5 - Система управления шагающего аппарата
   
   
   
   1. Модуль шести идентичных генераторов шаговых циклов. Выходом модуля являются шесть вектор функций - прообразы траекторий концов шести ног аппарата, поступающие в блок линейных преобразований системы управления, а также сигналы перехода каждого генератора из фазы переноса в фазу опоры и из фазы опоры в фазу переноса, поступающие в блок маневрирования.
      Входами модуля генераторов являются постоянные и настроечные параметры генератора, определяющие геометрические и временные характеристики шаговых циклов, задаваемых модулем параметров.
   2. Модуль формирования последовательности движении конечностей содержит перепрограммируемое запоминающее устройство (ППЗУ), в котором хранятся базовые матрицы регулярных походок); и процессов перестроения походок, а также набор временных и фазовых параметров, характеризующих походки и процессы перестроения походок. Кроме ППЗУ, модуль содержит устройство микропрограммного управления. Выходы модуля, управляющие переходом конечностей с фазы опоры в фазу переноса, поступают в модуль генераторов, параметры походок — в модуль параметров.
   3. Генератор ритма формирует тактовые сигналы, поступающие на вход модуля формирования последовательности движения конечностей. Входами генератора ритма являются выходы модуля параметров и сигналы верхнего уровня.
   4. Модуль параметров представляет (собой вычислитель для определения текущих значений части параметров генераторов шаговых циклов и генератора ритма как функций параметров, заданных верхним уровнем, модулем последовательности движений конечностей и текущих значений выходов генераторов шаговых циклов. Основой модуля являются устройства микропрограммного управления и ППЗУ .В состав также входят регистр выходной информации РВ, регистр связи с верхним уровнем РС и регистр адреса РА. Функциональная схема модуля показана на рисунке.
   
   
   PC - регистр связи с верхним уровнем; УМУ- устройство микропрограммного управления; РВ — регистр выхода; РА - регистр адреса;
   ППЗУ — перепрограммируемое запоминающее устройство
   
   Рисунок 6 - Структурная схема блока формирования последовательности движения конечностей
   
   
   4.2 Разработка модуля формирования последовательности движения конечностей шагового аппарата
   
   В ППЗУ размером 256*8 хранятся микрокоманды, которыми определяется работа устройства микропрограммного управления и константы. Константы могут интерпретироваться как адреса ячеек ППЗУ.
   В процессе движения аппарата считывание очередной микрокоманды из ППЗУ осуществляется по тактовому сигналу. поступающего с выхода генератора ритма (на рисунке он обозначен CL).
   В начальный период времени (до начала движения) считывание начальных значений параметров и начального состояния аппарата, соответствующих выбранной походке, осуществляется по управляющему сигналу, поступающему с верхнего уровня системы управления. На рисунке этот сигнал обозначен INIT. С целью упрощения реализации устройства микропрограммного управления (УМУ) приняты следующие ограничения: а) начальное состояние аппарата для движения заданной походкой известно заранее и совпадает с одним из столбцов базовой матрицы этой походки; б) базовые матрицы переходов с одной походки на другие состоятся так, что переход начинается из одного и того же состояния базовой матрицы исходной походки, а параметры меняются скачком в течение перехода.
   
   Последовательности смены состояний аппарата при движении регулярными походками и при переходах с одной из них на другую записываются в ППЗУ в виде микропрограмм, состоящих из микрокоманд.
   Имеются четыре различные микрокоманды. Задаваемые микрокомандой действия определяются значениями двух старших разрядов микрокоманды. Код, состоящий из шести младших разрядов микрокоманды, всегда поступает в выходной регистр блока в качестве значений . Чтение микрокоманд осуществляется в порядке возрастания адресов, если только адрес следующей ячейки не задается самой микрокомандой. В зависимости от состояния двух старших разрядов микрокоманды задают следующие действия:
   0-0 - нет действия;
   0-1 - записать в регистр адреса содержимое ячейки; 1-0 - при наличии сигнала «перепостроение походки » записать в регистр связи с верхним уровнем, в отсутствие этого сигнала микрокоманда 1-0 эквивалентна команде 0-0;
   1-1 - прочитать четыре последовательных ячейки, содержимое первых трех ячеек вывести в регистр выхода в качестве значений , содержимое четвертой записать в регистр адреса.
   
   Рассмотрим последовательности движения конечностей. Изначально в ППЗУ блока записаны микропрограммы, обеспечивающие последовательные смены состояний в соответствии с заданными регулярными походками и переходами с одной из них на другую, микропрограммы выхода из заданного начального начального состояния на одну из регулярных походок и соответствующие им константы. Кроме того, изначально в регистре адреса содержится адрес нулевой ячейки, в которой записан код 10 000 000.
   В начальный момент с верхнего уровня поступают сигнал «перестроение походки», адрес начала микропрограммы перехода из заданного начального состояния на желаемую походку и управляющий сигнал INIТ. При этом адрес начала микропрограммы записывается в регистр адреса. По второму сигналу INIТ верхнего уровня выполняется микрокоманда с кодом 1—1 (в микропрограмме перехода). В результате задаются начальное состояние и требуемые значения параметров . Вслед за этим управление передается микропрограмме, реализующей заданную регулярную походку, и сигнал «перестроение походки» снимается.
   Таким образом,микропрограмма выхода из заданного начального состояния имеет вид:
   
   
   где - ее адрес, - адрес микропрограммы регулярной походки.
   
   Микропрограмма для походки «галоп» имеет следующий вид;
   
   ,
   где — столбцы базовой матрицы походки «галоп».
   
   Микропрограммы, реализующие другие регулярные походки, построены аналогично. Рассмотрим работу блока и режиме перестроения походок. Когда оператор пли верхний уровень системы управления принимает решение о переходе с одной походки на другую, выдается сигнал «перестроение походки» и задается адрес микропрограммы перехода. При выполнении микрокоманды с кодом 1—0 адрес микропрограммы перехода будет записан в регистр адреса, и ее выполнение начнется со следующего такта. При этом и выходной регистр блока последовательно поступать, значения , соответствующие базовой матрице данного перехода. Одной из микрокоманд в микропрограмме перехода будет команда с кодом 1—1. При ее выполнении происходит изменение значений на выходе блока. Одновременно выполнение этой микрокоманды служитсигналом верхнему уровню на снятие сигнала «перестроение походки». Об этом свидетельствует сигнал который появляется на время выполнения микрокоманды с кодом 1—1. Последней в микропрограмме перехода стоит микрокоманда безусловного перехода на микропрограмму, реализующую новую регулярную походку. Входами блока являются сигналы верхнего уровня системы управления: «перестроение походки» — GO; адрес начала микропрограммы перехода с одной походки на другую — N тактовые сигналы для считывания начальных состояний и начальных значений параметров и тактовые сигналы поступающие с выхода генератора ритма.
   Выходами блока являются функции управляющие моментами перехода в фазу переноса соответствующих конечностей аппарата, значения параметров , поступающие в блок параметров, и сигнал DONE, следующий в момент выполнения микрокоманды с кодом 1—1 и поступающий на верхний уровень системы управления.
   
   4.3 Разработка модуля генератора ритма
   
   Генератором ритма называется устройство, задающее интервалы времени между сменами состоянии конечностей аппарата. Эти интервалы формируются в виде промежутков времени, за которые точка с некоторой скоростью проходит отрезок фиксированной длины. Уравнения, описывающие работу генератора ритма, анологичны уравнениям, описывающим изменение координаты в генераторе шагового цикла:
   ,
   где - положение изображающей точки; -функции, выведенные соотношением
   
   
   - скорость движения изображающей точки- параметр генератора шагового цикла; - параметр, определяющий длину отрезка, по которому движется изображающая точка;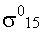 - время запаздывания срабатывания элементов сравнения Электрической схемы, реализующий уравнения, -вспомогательная переменная.
   Для формирования последовательности моментов времени с интервалами, равными , с помощью генратора ритма, как и в генераторе шаговых циклов, необходимо задать и доопределить на отрезке . Промежутки времени между сменами состояний конечностей аппарата формируются между двумя изменениями функции из 0 и 1. Управлять длительностью промежутков времени, задаваемых генератором ритма, можно с помощью . Из определения регулярных походок следует, что при фиксированных за промежутки времени, продолжительность которых в обобщенном времени равна , точка, двигающаяся со скоростью, пропорциональной проходит отрезки пути одной и той же длины. Поэтому в случае формирования последовательности моментов времени с интервалами, равными в обобщенном времени для регулярных походок, удобно задавать значение в виде
   
   - скорость изменения в фазе опоры; - параметр походки; параметры генератора шаговых циклов;
   
   
   
   Рисунок 7 - Функциональная схема генератора ритма
   , — интервал обобщенного времени, в течение которого все конечности аппарата находятся в фазе опоры. В этом случае, если пренебречь запаздыванием срабатывания элементов сравнения электрической схемы, можно показать, что
   
   Очевидно, что при заданных значение определяется однозначно. Входными сигналами генератора ритма являются значения, где задаваемые с пульта оператора или верхнего уровня системы управления, и значения формируемые блоком параметров.
   Выходом генератора ритма является сигнал поступающий на вход модуля формирования последовательности движения конечностей аппарата и качестве тактового сигнала.Работа генератора описывается уравнениями:
   
   
   Для формирования последовательности моментов времени с интервалами равными и доопределить на . Управление длительностью промежутков времени осуществляется с помощью - параметр генератора шаговых циклов.
   
   4.4 Разработка модуля параметров
   Блок параметров (структурная схема блока приведена на рисунке как отмечалось ранее, представляет собой вычислитель для определения текущих значений как функций параметров, задаваемых верхним уровнем, блоком последовательности движения конечностей и текущих значений выходов генераторов шаговых циклов.
   
   Рисунок 8 - Структурная схема блока параметров
   Кроме того, блоком параметров задаются значения настраиваемых параметров , определяющих геометрические размеры шаговых циклов. Так как значения этих параметров не меняется при переходе от одной походки к другой, их конкретные значения выбираются в процессе настройки блока и впоследствии не меняются.
   Для вычисления текущих значений ,на входы блока параметров поступают:,с верхнего уровня;, с выхода блока формирования последовательности движения конечностей; текущие значения ,с выхода блока генераторов шаговых циклов. Так как движению конечностей аппарата соответствует последовательное чередование фазы опоры и фазы переноса, а их положение в момент перехода не фиксировано, значения ,могут меняться от шага к шагу и вычисляются на соответствующих фазах переноса для каждой конечности аппарата отдельно в моменты времени, когда изображающие точки, описывающие движение соответствующих концов ног, переходят с участка 2 на участок 3 траектории шагового цикла. В эти моменты ,меняет значение с 1 на 0. Значения ,определяются из соотношения
   ,
   где = 1, 2, .... 6 — номер ноги (см. рисунок );j = 1, 2, 3,... — номер шага;, — значение , в момент изменения из 1 в 0 на шаге с номером j Значение вычисляется в соответствии с выражением:
   
   На основе этого выражения с учетом соотношения получаем
   
   Входами блока параметров, как было отмечено выше, являются: параметры, поступающие с выхода блока формирования последовательности движения конечностей аппарата и определяющие фазовые соотношения между их движениями; —скорость движения изображающих точек в генераторах шаговых циклов на фазе опоры, поступающая с верхнего уровня системы управления;, — выходы блока генераторов шаговых циклов.
   Выходами блока параметров являются значения используемые в генераторах шаговых циклов, а также значения поступающие на вход генератора ритма.
   Разработанный блок формирования походок шагающего аппарата реализуется в виде спецвычислителя. Для его реализации использовались элементы цифровой и аналоговой техники.
   
   Математическое моделирование динамики движения шестиногого шагающего аппарата
   
   
   При движении аппарата по склону корпус аппарата движется параллельно опорной поверхности. Рассматривается движение аппарата походкой, называемой «трешками».
   Предполагается, что наступание на поверхность происходит стопой безударно. Максимальная величина подъема ноги равна h. Изменение углов в шарнирах ног осуществляется электродвигателями постоянного тока, соединенными соответствующими звеньями ног через редукторы.
   
   Рисунок 9 - Кинематика ноги.
   
   Обозначим угол поворота якоря двигателя в j-том шарнире i-той ноги α_ij;
   
   где - коэффициент редукции в j-ом шарнире i-той ноги. Механическое уравнение электродвигателя постоянного тока в j-ом шарнире i-той ноги имеет вид:
   
   ,
   где - момент инерции якоря двигателя,
   - электромагнитный момент двигателя,
   - момент нагрузки на валу двигателя,
   - постоянный по величине момент сухого трения на валу двигателя,
   - постоянный по величине момент потерь в редукторе,
   - определяется через момент в шарнире ноги.
   Электромеханические уравнения движения электродвигателей постоянного тока в шарнирах ног в предположении безиндуктивности двигателей имеют вид:
   ,
   - напряжение, ток, сопротивление в цепи якоря,
   - электрическая и магнитная постоянная двигателя.
   Данные уравнения позволяют вычислить динамические характеристики движения двигателей в шарнирах ног, по значениям координат, скоростей, ускорений аппарата и значениям моментов в шарнирах ног.

В работе исследована динамика движения шестиногого шагающего гиппотетического аппарата, который задан линейными размерами и масс-инерционными характеристиками.

Приведен обзор видов походок шестиногого шагающего аппарата.
Даны диаграммы походок,вектор-финкция походок.

Представлены: типы опорных поверхностей и их характеристика по несущей способности, характеристики грунтовых поверхностей по сопротивлению деформированию под нормальной нагрузкой от опор ШМ, характеристика опорных поверхностей движения по сцеплению с ними опор ШМ, виды неровностей и препятствий на опорных поверхностях перемещения ШМ.
Записана математическая модель блока формирования походки.

Блок состоит из: Модуля шести идентичных генераторов шаговых циклов. Выходом модуля являются шесть вектор функций - прообразы траекторий концов шести ног аппарата. Модуль формирования последовательности движении конечностей содержит перепрограммируемое запоминающее устройство (ППЗУ), в котором хранятся базовые матрицы регулярных походок); и процессов перестроения походок, а также набор временных и фазовых параметров, характеризующих походки и процессы перестроения походок. Кроме ППЗУ, модуль содержит устройство микропрограммного управления. Генератор ритма формирует тактовые сигналы, поступающие на вход модуля формирования последовательности движения конечностей. Входами генератора ритма являются выходы модуля параметров и сигналы верхнего уровня. Модуль параметров представляет (собой вычислитель для определения текущих значений части параметров генераторов шаговых циклов и генератора ритма как функций параметров, заданных верхним уровнем, блоком последовательности движений конечностей и текущих значении выходов генераторов шаговых циклов. Представлена Функциональная схема блока формирования походок. Записана математическая модель траектории шагового цикла, ее графическое представление, с описанием фаз. Описаны уравнения позволяющие вычислить динамические характеристики движения двигателей в шарнирах ног, по значениям координат, скоростей, ускорений аппарата и значениям моментов в шарнирах ног.

1. Охоцимский Д. Е., Платонов А. К., Математическое маделирование джинамики движения шагающего аппарата.: Препринт Ин-та прикл. математики АН СССР № 96. М., 1984. 28 с.
2. Шахинпур М.А., Курс робототехники: пер с англ. - М.: Мир, 1990. - 527 с.
3. Динамика и управление движением многоногих статически устойчивых шагающих машин.
   Результаты выполнения работ по федеральной целевой программе "Интеграция науки и высшего образования России на 2002-2006 годы". http://dtm.vstu.ru/research/walkingmachines/walkingmachinesr.html
   
4. Макаров И. М., Охоцимский Д. Е., Попов Е. П., Исследование робототехнических систем. Сб. научных статей., М. : Наука, 1982. 246с.

   ---

   En Ua Ru ДонНТУ Магистратура ДонНТУ Ссылки Библиотека Результаты поиска Инд задание
   

   ---