PETSc - Набор процедур и структур данных для параллельного решения научных задач с моделями, которые описываются в виде дифференциальных уравнений с частными производными. Предлагает линейные решатели, реализованные с помощью точечного и блочного алгоритма Якобе, аддитивного метода, с помощью LU-, QR-развития, метода Крылова и др. А также - нелинейные решатели, построенные по методу Ньютона.

    Задача разработки решателей для сетевого динамического объекта (МДО) является следующей: для системы, сформированной генератором уравнений в виде, требуемом средствами моделирования и отражающем описание топологии сетевого динамического объекта, разработать алгоритмы и программы решения, основанные на последовательных и параллельных численных методах.

     Цель работы - разработать последовательную и параллельную имплементацию решателя уравнений, используя параллельный блочный численный метод.

     Среди ряда задач, поставленных для достижения цели, можно выделить следующие:

Сетевой динамический объект с распределенными параметрами как объект моделирования

     Сетевые объекты используются во многих областях техники. Примерами таких объектов могут быть электрические сети, нефтепроводы и др. Объектом исследования является шахтная вентиляционная сеть (ШВС) [2].

    Сетевые объекты относятся к сложным динамическим системам, так как имеют большую размерность, нелинейность характеристик и распределенные относительно пространственных координат параметры.

    Все динамические системы можно разделить на два класса:
-     системы с сосредоточенными параметрами;
-     системы с распределенными параметрами

    Системы с сосредоточенными параметрами описываются с помощью конечного количества алгебраических и обычных дифференциальных уравнений для переменных, которые зависят от времени. Системы с распределенными параметрами описываются с помощью дифференциальных уравнений в частных производных. Здесь переменная состояния в каждый момент времени – это функция относительно одной или нескольких координат пространства. В дальнейшем будем рассматривать переходные аэродинамические процессы в ШВС, элементы которой рассматриваются как объекты с распределенными параметрами.

    Топология сетевого объекта представляется в виде графа. Каждый сетевой объект зависит от внешних предельных условий. К ним относятся давления в начальных узлах, соединенные с атмосферой, и давления в узлах, к которым подключены вентиляторы, создающие постоянное давление. Если рассматривать отдельную ветвь с индексом i, то процессы изменения значения потока воздуха Q_i и давления P_i представляются в виде следующих уравнений [2]:

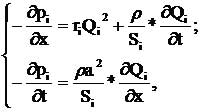
где P_i– значение давления в і-ой ветви; r_i – удельное аэродинамическое сопротивление;
а – скорость звука в воздухе; S_i – площадь сечения ветви;
х – координата вдоль ветви.

    После аппроксимации этих уравнений по методу прямых [1] получаем следующие системы уравнений для j-го элемента ветви, дискретной с шагом :

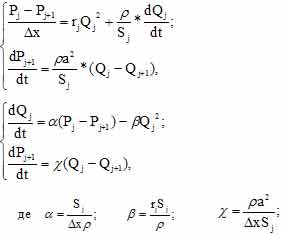
    Для моделирования ШВС необходимым шагом является выбор численного метода. Известными являются следующие:
- метод Ейлера;
- метод Адамса-Башфорта;
- метод Рунге-Кутта;
- блочные методы.

    Первые три численных метода имеют одну общую черту – они основываются на последовательных алгоритмах вычисления. Последний метод предоставляет возможность нахождения нескольких значений потока воздуха и давления одновременно, что является актуальным для решения таких сложных задач с большим объемом вычислений и может значительно уменьшить продолжительность расчетов.

Параллельный блочный численный метод

Параллельные блочные численные методы решают задачу Коши. Для одного обычного дифференциального уравнения первого порядка задача Коши имеет следующий вид [1]:

    Параллельные блочные численные методы решения задачи Коши делятся на одношаговые и многошаговые методы. На рис. 1 приведенная схема разбиения на N блоков одношагового k-точечного метода.

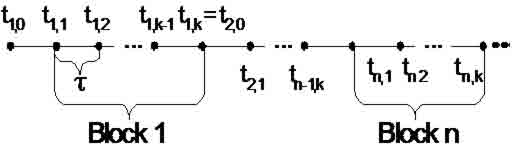
Рисунок 1 – Схема разбиения на блоки одношагового k-точечного метода

    В ходе численного решения задачи Коши для каждого следующего блока новые k значений вычисляются одновременно. На рис.2 представлен шаблон одношаговой k-точечной разностной схемы.

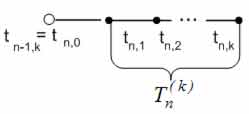
Рисунок 2 – Шаблон одношаговой k-точечной разностной схемы

    Формула для вычисления новых k значений:

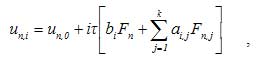
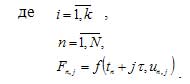
    Для определения коэффициентов a_i,j и b_i надо построить интерполяционный многочлен Лагранжа L_k(t) с узлами интерполяции t_n , i, i = 0,1,…,k и соответствующими им значениями F_n,i = f(t_n, i, u_n, i) и проинтегрировать в границах (t_n, t_n + i* ) . Для двухточечного блочного метода значения в каждой точке n-блока необходимо вычислять по следующим формулам:

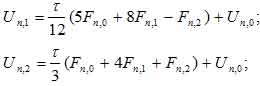
Пример вычисления одной ветви ШВС блочным численным методом.

    Рассмотрим небольшую ветвь ШВС, которая состоит лишь из четырех узлов.

    Предположим, что начальный узел соединен с атмосферой, а к последнему подключены вентиляторы, которые создают постоянное давление в ветви. Таким образом, значение давления в начале и в конце ветви является постоянным. Процессы изменения значения потока воздуха Q и давления P представляются в виде следующих уравнений:

    Решим эту систему уравнений параллельным блочным одношаговым двухточечным методом (k=2). На рис.3 показано, каким образом подветви разбиваются на блоки по этому методу.

Рисунок 3 – Разбивка подветви на блоки одношаговым двухточечным методом

    Значение потока воздуха Q и давления P в каждой точке блока исчисляются по формулам:

    Необходимо указать, что дополнительный индекс q является порядковым номером уравнений в системе. U_n,q,0 – это значение потока воздуха Q или давления P в начальной точке блока. В первом блоке эта переменная равняется начальным входным данным для потока воздуха Q или давления P. В следующих блоках переменная U_n,q,0 имеет значение U_n-1,q,2. Вычислим значение потока воздуха Q₁(1) в точках блока.

    Вычислим значение потока воздуха P₂(2) в точках блока.

    Решение такой системы в явном виде является невозможным из-за взаимозависимости правых и левых частей уравнений. Вычислить такую систему уравнений можно с помощью итерационного метода. На первой итерации находится приблизительное значение U_n,q,1 и U_n,q,2 , а с каждой следующей итерацией это значение уточняется. Предположим, что S – это номер итерации. В общем виде количество итераций должно равняться количеству точек в блоке
    Первая итерация(S=0):

где і – номер точки (і=1..2), U_n,q,i⁽⁰⁾ – значение U_n,q,i на первой итерации.

    Следующая итерация (S=S+1):

Последовательный алгоритм вычисления одной ветви ШВС блочным численным методом.

    На рис.4 приведен общий последовательный алгоритм вычисления одной ветви ШВС параллельным блочным одношаговым двухточечным методом для одного блока.

Рисунок 4 – Общий последовательный алгоритм вычисления одной ветви ШВС параллельным блочным одношаговым двухточечным методом для одного блока

     Был проведен ряд модельных экспериментов, целью которых было установить работоспособность последовательной имплементации блочного одношагового двухточечного метода и сравненить ее с последовательной программой, которая реализует метод Адамса – Башфорта. Объектом моделирования является тестовая выработка ШВС со следующими аэродинамическими параметрами: длина одной ветви L = 2000 м, площадь сечения ветви S=7 м², удельное аэродинамическое сопротивление r_уд = 0.00048 Hc²/м⁹.

    Другими характеристиками дискретной модели выработки являются: М – количество элементов длиной , на которые разбивается выработка; – временной шаг аппроксимации уравнений численным методом.
    По результатам проведенных экспериментов можно получить следующие выводы:

1. Увеличение или уменьшение временного шага аппроксимации уравнений приводит к изменению характера процессов Q₁(t) и Q_M(t) при фиксированном значении количества узлов М в одной ветви и скачкообразном Р(t). От точности выбора временного шага аппроксимации уравнений зависит эффективность и скорость протекания технологического процесса. Иначе процессы Q(t) могут пойти в разнос.

2. Увеличение количества узлов М в одной ветви приводит к увеличению времени продолжительности технологического процесса.

3. Реализация поставленной задачи блочным численным методом, по сравнению с методом Адамса-Башфорта, дает больший выигрыш во времени (приблизительно в два раза).

    Разработанный последовательный алгоритм вычисления одной ветви ШВС параллельным блочным одношаговым двухточечным методом и исследование его результатов является первым шагом к построению параллельного МІМD-решателя сетевого динамического объекта.

Подход к распараллеливанию решателя для СДО.

     На рисунке 5 представлены четыре возможных уровня распараллеливания. Обмен данными между процессами осуществляется с помощью механизма обмена сообщениями MPI (Message Passing Interface) [5].

     На самом низком уровне каждый процесс занимается решением лишь одного уравнения. На втором уровне процессу отводится решение отдельного участка ветви. На третьем уровне параллельно рассчитывается каждая ветвь или узел. И на последнем уровне граф МДО разбивается на отдельные части.

Рисунок 5 – Уровни распараллеливания сетевых динамических объектов.

     В случае распараллеливания ШВС на первом уровне, получаем следующую схему обмена данными между процессами:

     Если подняться ко второму уровню распараллеливания, на котором каждый процесс будет рассчитывать значение потока воздуха Q_i и давления P_i, то схема обмена данными между процессами несколько изменится:

    После сравнения приведенных выше схем можно увидеть, что количество обменов данными между процессами на двух уровнях распараллеливания одинаково. Таким образом, время передачи данных на втором уровне распараллеливания ШВО уменьшится в два раза.

Заключение

В работе была разработана последовательная имплементация блочного одношагового двухточечного метода, был проведен ряд экспериментов для сравнения ее с последовательной программой, которая реализует метод Адамса – Башфорта.

    Разработаны параллельные имплементации вычисления одной ветви ШВО блочным методом на первых двух уровнях распараллеливания.

     Далее планируется провести исследование последних двух уровней распараллеливания всего моделирующего объекта и ряд экспериментов, относительно эффективности и способов распараллеливания именно блочного численного метода.

Список литературы

1. Фельдман Л.П., Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці. – К.:Видавнича група ВНV, 2006. – 480с.
2. Абрамов Ф.А., Фельдман Л.П., Святный В.А. Моделирование динамических процессов рудничной аэрологии.К.:Наук.думка, 1981.–284с.
3. Святный В.А., Молдованова О.В., Перерва Л.О. Проблемно орієнтоване паралельне моделююче середовище для динамічних мережних обє’ктів. Наукові праці ДонДТУ, серія «ІКОТ», вип. 29, 2001, с 246-253.
4. C/C++. Программирование на языке высокого уровня / Т.А. Павловская. – СПб.: Питер, 2004. – 461 с.
5. MPI 2.0 Standart www.mpi-forum.org/docs