Network dynamic object with the distributed parameters as object of simulation

    Network objects are used in many areas of technics. Examples of such objects can be electric networks, oil pipelines, etc. Object of the research is the mine ventilating network (MVN) [2].

     Network objects concern to complex dynamic systems through greater dimension, nonlinearity of characteristics and they are distributed concerning spatial coordinates parameters.

    All dynamic systems can be parted into two classes:
- systems with the concentrated parameters;
- systems with the distributed parameters.

    Systems with the concentrated parameters are described by means of finite number of the algebraic and ordinary differential equations that are depended on time variables. Systems with the distributed parameters are described by means of the partial differential equations. Here the condition variable during each moment of time is a function of one or several coordinates of space. In the further it will be considered a transitive aerodynamic processes in MVN which elements are considered as objects with the distributed parameters.

    The topology of network object is represented in the form of the graph. Each network object depends on external limiting conditions. To this conditions concern the pressure in an initial node, which is connected with an atmosphere, and pressure in nodes to which the creating constant pressure fans are connected. If it will be considered a separate branch with an index i, then processes of an air flow Q_i and pressure P_i changing are represented in the form of the following equations [2]:

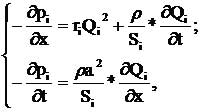
where P_i– value of pressure in і-th branch; r_i – specific aerodynamic resistance;
а – speed of a sound in air; S_i – the area of a branch section;
х – coordinate along a branch.

    After approximation of these equations by a method of straight lines [1] it is derived following equations systems for j-th element of a branch:

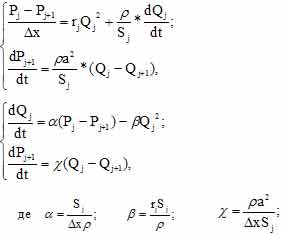
    For MVS simulation it is necessary to choose of a numerical method. There is known following numerical methods:
- Euler method;
- Adams-Bashfort method;
- Runge-Kutta method;
- block methods.

    The first three numerical methods have one general feature. They are based on sequation computing algorithms. Last method gives an opportunity for finding of several value of pressure air flow, that is actual for the solution of such complex problem with great computing volume and can reduce the duration of computing.

Parallel block numerical method

Parallel block numerical methods solve Cauchy problem. Cauchy problem has a following appearance for one ordinary differential equation of the first order [1]:

    Parallel block numerical methods of the Cauchy problem decision is divisible by single-step and multistage methods. On figure 1 it is shown the scheme of a single-step k-point method on N blocks splitting.

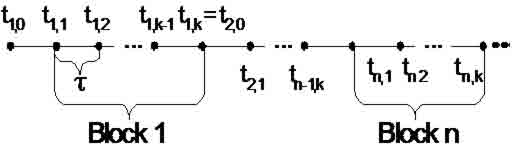
Figure 1

     New k values are calculated simultaneously for each following block during the numerical solution of Cauchy problem . On figure 2 the pattern of single-step k-point finite-difference schemes is presented.

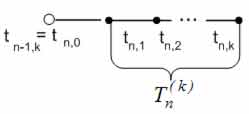
Figure 2

    The formula for calculation new k values is following:

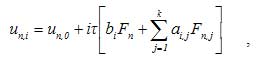
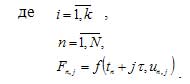
    For the solution of factors a_i,j and b_i it is necessary to construct construct Lagrange interpolating polynomial L_k(t) with nodes of interpolation t_n , i, i = 0,1,…,k and values F_n,i = f(t_n, i, u_n, i) corresponding them, and to integrate in boundary (t_n, t_n + i* ) . Values in each point of the n-block for a two-point block method are necessary to calculate under following formulas:

Sequential algorithm of one branch MVS computing by the block numerical method

    On figure 3 it is resulted the general Sequential algorithm of one branch MVS computing by the parallel block single-step two-point method for one block.

Figure 3

    It was leaded a number of modeling experiments. The purpose of them was establishment of sequential implementation working of a block single-step two-point method and comparison it with the sequential program that realized the Adams-Bashfort method. Object of simulation is benchmark mine working with following aerodynamic parameters: length of one branch L = 2000 m, the area of section of branch S=7 m², specific aerodynamic resistance r_sr = 0.00048 Ns²/m⁹.

    Other characteristics are: M - quantity of elements in length , into which one mine branch is divided; – a time step of the equations approximation by numerical method.

    By results of the experiments it is possible to become following conclusions:

1. The increase or reduction of equations approximation time step leads to change of processes Q₁(t) and Q_M(t) character when the value of M nodes number in one branch is fixed and Р (t) is jumping. Efficiency and speed of technological process passing depend on accuracy of a time step equations approximation choice. Otherwise processes Q (t) can go in overrun.

2. The Increase of node number M in one branch leads to increase of technological process time duration.

3. Realization of a task by a block numerical method, in comparison with the Adams-Bashfort method, gives a greater gain in time (approximately by a factor of two).

The approach to paralleling of solver for NDO

     In figure 4 it is shown four possible levels of paralleling. Data exchange between processes is carried out by means of MPI (Message Passing Interface) [5].

     At the lowest level each process is engaged in the decision of only one equation. At the second level process calculate a separate part of a branch. Each branch or node is calculated at the third level. And at last level NDO graph divide into separate parts.

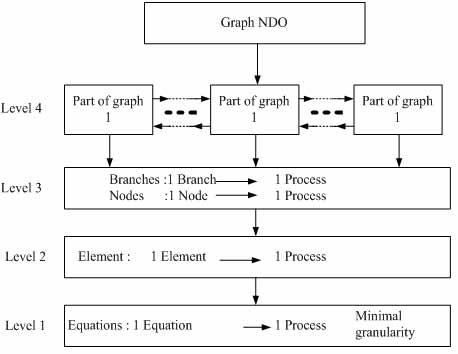
Figure 4

The conclusion

In work it has been developed sequential implementation of a block single-step two-point method, has been lead a number of experiments for its comparison with the consecutive Adams-Bashfort method.

     It was developed a parallel implementations of MVO for one branch at first two paralleling levels by a block method.

     Further it is planned to research two last paralleling levels of all simulated object and leaded a number of experiments, that will be concerned to efficiency and ways of a block numerical method paralleling.

Literature

[1] L.P. Feldman, A.I. Petrenko, O.A. Dmitrieva.
     "Numeric methods in informatics", 2006.
[2] F.A.Abrmov, L.P. Feldman, V.A. Svyatniy.
     "Dynamics processes simulation of mine aerology", 1981
[3] V.A. Svyatniy., O.V. Moldovanova, L.O. Pererva.
     "Problem-oriented parallel sumulation environment for dynamics network objects", 2001.
[4] MPI 2.0 Standart www.mpi-forum.org/docs