| ДонНТУ | Портал магистров ДонНТУ | РУС | ENG |
| Автобиография | Отчёт о поиске | |
| Библиотека | За полярным кругом | Ссылки |
Дыхно М. В.  giveman@mail.ru giveman@mail.ru |
Автореферат магистерской работы на тему:«Исследование методов поиска грубых ошибок измерений при уравнивании сетей съемочного обоснавания топографических съёмок»Научный руководитель: Зав.кафедрой, профессор, д.т.н., Могильный Сергей Георгиевич |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Актуальность темыНаличие грубых ошибок в геодезических измерениях всегда влекло за собой какие-то временные, а значит и материальные затраты. Поэтому и поиск измерения, содержащего ошибку здесь очень важен и остается актуальным и по сей день . А в настоящее время еще и очень стремительными темпами развиваются автоматизированные системы и технологии сбора и обработки геодезической информации. И при этом тоже существует очень большая вероятность того, что данные будут содержать ошибки, то ли это вследствие человеческой деятельности, то ли вследствие сбоев программного обеспечения. Цель исследования и планируемый практический результатИз темы моей работы вытекает следующие цели и задачи: 1) изучить и проанализировать существующие методы поиска грубых ошибок применительно к сетям съемочного обоснования топографических съёмок; 2) экспериментальным путём определить на сколько надежно тот или иной метод способен обнаруживать грубые ошибки; 3) проанализировать полученные результаты. Теперь необходимо точно дать определение понятию «поиск грубых ошибок». Это прежде всего комплекс мероприятий направленных на определение величин грубых ошибок и измерений, в которых они содержатся с точностью до подгруппы из k измерений ( k << n , в предельном случае k =1). Но здесь есть одно «но» - изучая литературу, я наткнулся на статью Юрия Исидоровича Маркузе, зав. кафедрой геодезии Московского государственного университета геодезии и картографии, в которой он приводит доказательство, того что для грубых ошибок, которые могут быть обнаружены, существует теоретическая граница – их количество не может быть больше r где r – число избыточных измерений, а в типичном разомкнутом линейно-угловом ходе число избыточных измерений, как известно равно 3, в нестандартном ходе их может быть и больше и меньше трёх. Необходимо определить какие результаты уравнивания могут служить для поиска грубых ошибок? Такими результатами являются поправки в измерения, потому что, как известно, при наличии в измерениях грубых ошибок поправки недопустимо велики. Чтобы выяснить, почему так происходит, необходимо рассмотреть механизм формирования поправок и влияние грубых ошибок на поправки. Для вывода можно воспользоваться формулами параметрического способа уравнивания, так как поправки не зависят от способа уравнивания
Как видно при случайном векторе невязок измерений L стоит матрица, элементы которой при данной конфигурации сети являются постоянными величинами. Поэтому можно сделать вывод о том, что эта матрица и определяет собственно правила формирования поправок для данной сети. Обозначим эту матрицу через G . Тогда формула (1) будет:
Выделим из формулы (2) i -тую поправку: где lr - элемент вектора ошибок измерений, содержащий грубую ошибку. Здесь видно, что ошибочное измерение влияет на все поправки и влияет в мере, определяемой коэффициентом, стоящим перед данным ошибочным измерением Из этого следует очень важный вывод – не всегда максимальная поправка соответствует измерению с промахом. Необходимо учитывать матрицу G . Таким образом мы подошли к методам определения грубых ошибок, использующих матрицу G в своих выводах. Обзор состояний исследований и разработок по теме1- й метод . Метод наложения графиков. Рассмотрим метод, предложенный Дъяковым Б. Н. и Родионовой Ю. В. в статье [1]. Сущность метода основана на использовании всех элементов матрицы G . Если какое-либо измерение содержит грубую ошибку lj , то поправки во все измерения вследствие этой ошибки будут:
где g i,j , — элементы j -го столбца G-матрицы. Реальные поправки измерений Vi отличаются от величин vi,j , но эти отличия будут невелики, так как математическое ожидание суммарного влияния остальных случайных ошибок на каждую поправку в отдельности равно нулю. Чтобы выделить грубое измерение, достаточно при вычисленном значении грубой ошибки j -го измерения bj = Vj / gi,j подсчитать для всех n измерений среднее квадратическое отклонение поправок Vi, от величин vi,j по формуле:
После тестирования всех измерений грубым признается то, для которого значение dj окажется наименьшим. Для наглядности можно построить графики поправок из уравнивания Vj и величин vi,j и наложить один на другой. Для грубого измерения совпадение графиков будет наилучшим. При тестировании на две грубые ошибки их предварительные значения D j и D k нужно находить из решения системы двух уравнений (3), а среднее квадратическое отклонение dj,k подсчитывать по формуле:
Для пары измерений, содержащих грубые ошибки, величина dj,k должна иметь минимальное значение. [1].
2- й метод .Профессор Коугия В.А. исследовал возможность идентифицировать грубую ошибку по значению поправок, то есть определить измерение, в котором она содержится, и сделал вывод о том, что для измерения, содержащего грубую ошибку, отношение поправки к допуску имеет максимальное значение, то есть он основан на определении нормированной поправки vi /mvi . Для того чтоб ы найти СКО поправки m vi необходимо определить корреляционную матрицу поправок. Как известно на диагонали стоят СКО поправок.
Или матрицу можно представить виде:
Как видно матрица G тоже влияет на формирование элементов матрицы Kv. Рассмотрим подробнее. На основании (5), полагая измерения независимыми, запишем:
Подставим последнее выражение в (2) и заменим случайные ошибки измерений их математическими ожиданиями, равными нулю. Получим математическое ожидание вектора поправок:
Отношение математического ожидания i-той поправки к допуску будет:
где ri,h - коэффициент корреляции i-той и h-той поправок, постоянная
Модули коэффициентов корреляции меньше либо равны единице для всех значений i. Следовательно, для измерения, содержащего грубую ошибку, отношение поправки к допуску имеет максимальное значение и может служить признаком для отбраковки этого измерения. Среди поправок, вышедших за границы допусков, грубая ошибка содержится в тех измерениях, где отношение модуля поправки к допуску наибольшее [2]. Параметрический способ уравнивания удобен для программирования. Поэтому исследования будем выполнять с помощью этого метода уравнивания. Выберем линейно-угловой ход произвольной формы. Для исследования нам необходимо составить или смоделировать несколько таких сетей. Необходимо в каждое измерение добавить случайную ошибку. И эти ошибки должны быть такие, чтобы суммарное влияние на результаты уравнивания были равны нулю. В этом может помочь метод имитационного моделирования, алгоритм которого заключается в следующем: 1) сгенерировать случайную величину, распределённую по нормальному закону распределения с математическим ожиданием, равным нуль и дисперсией равной проектному значению ошибки единицы веса для данного хода. 2) добавить эту величину в каждое измерение; 3) повторить данный пункт 100 раз и таким образом составить 100 вариантов сетей. 4) добавить в каждом из вариантов в одно или в два из измерений грубую ошибку. 5) уравнивание сети параметрическим способом; 6) анализ результатов уравнивания и идентификация грубых ошибок в каждом варианте по методике; 7) определение надёжности определения грубой ошибки, то есть подсчёт количества вариантов, для которых правильно идентифицированы грубые ошибки, а для этого необходимо сравнить результат идентификации и с информацией об истинном нахождении истинной ошибки. Для реализации методики нахождения грубых ошибок, как указывалось выше, необходимо сначала уравнять геодезическую сеть, так чтобы в результате получились поправки в измерения и средние квадратические отклонения этих поправок. В исследованиях использовались программа Mathcad и программный продукт «МГСЕТИ», разработанный на кафедре геоинформатики и геодезии Донецкого национального технического университета. Мои достиженияТаким образом, в процессе выполнения данной исследовательской работы для тестирования линейно-углового хода, представленного на рис.1, на надежность обнаружения грубой ошибки использовался Mathcad.
Рис 1 - Линейно-угловой ход произвольной формы (Анимация выполнена в Microsoft GIF Animator: 10 кадров, 5 циклов повторения, размер 45,1 Kb) Таблица 1 - Тесирование метода наложения графиков
Таблица 2 - Тесирование метода поправка/допуск
На этой сети исследования не прекратились. Была написана программа, реализующая методику поиска грубых ошибок, предложенную Коугия, в среде Delphi, использующая в качестве исходных данных результаты работы программного продукта «МГСЕТИ». В данном случае в качестве анализируемой геодезической сети была выбрана строительная сетка (рис. 2).
Рисунок 2 - Схема строительной сетки Программа была протестирована 10 раз. Результаты можно свести в таблицу:
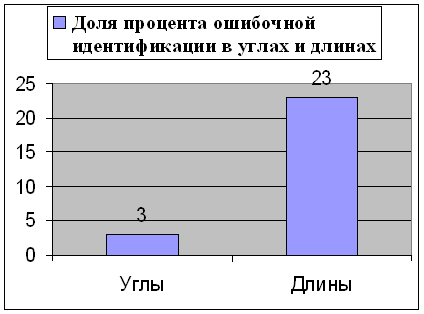
Отсюда можно сделать вывод, что методика обнаружения грубой ошибки по поправкам из уравнивания, предложенная профессором Коугия Вилио Александровичем, позволяетв 20-30 из 100 случаев не верно идентифицирует измерение, содержащее грубую ошибку. ВЫВОДЫ.Проанализировав результаты, можно сделать следующие выводы: • метод наложения графиков показал неудовлетворительные результаты 15% правильно найденных промахов, но этому доверять нельзя, так как недостаток может содержаться не в методике, а в программной его реализации, поэтому необходимы дальнейшие исследования; • методика профессора Коугия «поправка/допуск» дала хорошие результаты: - 93,5% для линейно-углового хода на рис.1; - 74% для строительной сетки (рис.2). Но во втором случае замечен очень странный факт: неправильная идентификация измерения, содержащего грубую ошибку, преобладает для измерений длин. Это отображено диаграмме.
Рисунок 3 - Диаграмма процент ошибочной идентификации в углах и длинах Направление дальнейших исследованийЭто явление необходимо дальше исследовать. Также дальнейшие исследования будут заключаться в анализе методов на возможность обнаружения нескольких грубых ошибок. Окончательный вариант изложенных выше исследований будет представлен в декабре 2008 года.
Перечень ссылок:1 . Дьяков Б.Н., Родионова Ю.В. Тестирование линейно-угловых ходов на грубые ошибки измерений // Геодезия и картография. – 2003. - №7. – с. 21-24. 2 . Коугия В.А. Сравнение методов обнаружения и идентификации ошибок измерений // Геодезия и картография. – 1998. - №5. – с. 23-27.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
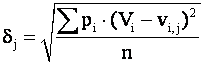 (4)
(4) (5)
(5)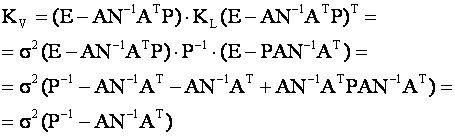
 (7)
(7) 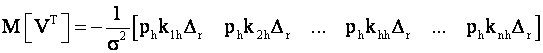 (8)
(8) (9)
(9)