Рудской Денис Станиславович

Факультет: Энергомеханики и автоматизации

Специальность: Подъемно-транспортные, строительно-дорожные, мелиоративные машины и оборудование

Тема выпускной работы:

Анализ и исследование динамического состояния стрелового крана в переходных режимах при подъеме груза

Руководитель: д.т.н. проф. кафедры ГЗТиЛ, Дворников Владимир Иванович

VII Международная научно-техническая студенческая конференция

"Механика жидкости и газа"

УДК 621.86

ВЫБОР ОПТИМАЛЬНОГО ЗНАЧЕНИЯ РЫВКА ПРИ ПОДЪЕМЕ ГРУЗА СТРЕЛОВЫМ КРАНОМ

Рудской Д.С., студент, Дворников В.И., докт. тех. наук., проф., Донецкий национальный технический университет

Исследована зависимость динамического состояния стрелового крана при подъеме груза от величины рывка.

Пусть груз перемещается так, что вначале он ускоряется, двига-ясь вниз, затем некоторое время движется с постоянной скоростью, после чего замедляется и, наконец, останавливается. По истечении времени паузы он начинает перемещаться в обратном направлении, проходя такие же стадии движения циклически.

Сказанное иллюстрирует диаграмма на рис. 1, на которой пока-зано изменение скорости и ускорения груза в течение одного цикла операции спуска-подъема. Здесь рывок в моменты изменения ускорений принят настолько большим, что в точках 0, 1, 2, 3 имеют место резкие «изломы» функции скорости и при этом ускорение изменяется «скачкообразно».

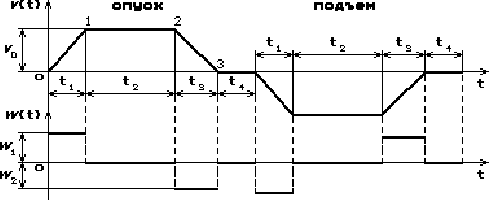
Рисунок 1 - Диаграммы скорости и ускорения без ограничения рывка

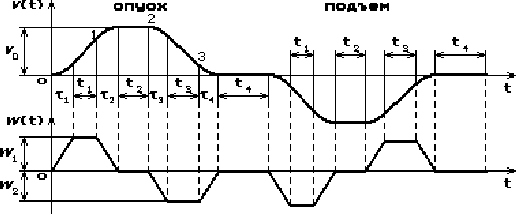
Рисунок 2 - Диаграммы скорости и ускорения с ограничением рывка

На рис. 2 показано изменение переменной скорости и ускорения груза при достаточно небольших рывках, обеспечивающих плавное изменение скорости в точках 0,1,2,3 (то есть на интервалах , , и ) и трапецеидальный характер изменения ускорений . Функция изменения рывка здесь также не показана, но можно сказать, что она представляет собой ступенчатую линию и отличается от нуля только на интервалах времени , , и .

Влияние величины рывка на динамическое состояние крана ото-бражено на рис 3. Кривая 1 построена, для варианта, когда все настолько велики, что диаграмма скорости (вверху на рисунке) состоит из одних ломаных линий. Кривая же 2 построена для случая, когда величины рассчитаны по формуле «оптимального рывка»

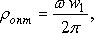
и при этом, как видно, полностью отсутствует колебательный характер функции перемещений. Сама же функция как бы копирует диаграмму ускорения что и подтверждает сказанное выше.

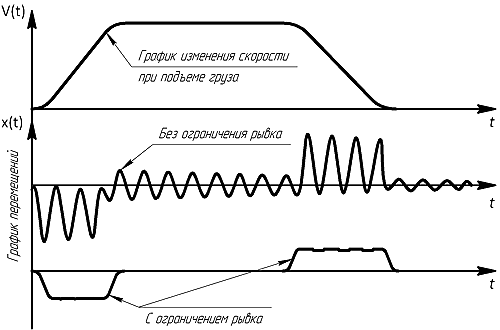
Рисунок 3 - Динамические процессы в момент подъема груза при различных значениях рывка

Список источников

1. Лобов Николай Александрович / Динамика грузоподъемных кранов, М.: Машиностроение, 1987. - 156 с.

2. Гелетий Владимир Николаевич / Разработка динамических моделей и совершенствование расчета башенных кранов. Автореф. дис., (01.02.06). – Львов, 1985. – 18 с.

3. Дворников Владимир Иванович / Конспект лекций по курсу «Динамика строительных машин», Макеевка 2001. - 63 с.