VIII Региональная научно-методическая конференция
"Машиностроение"
УДК 621.81
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ПЛОСКОГО РЫЧАЖНОГО МЕХАНИЗМА И ИХ ВЛИЯНИЕ НА УГЛЫ ДАВЛЕНИЯ
Гордиенко Э.Л., Рудской Д.С. (ДонНТУ, г.Донецк, Украина)
 В различных машинах находят применение рычажные механизмы, при работе которых ведомое звено должно в определенные моменты времени занимать заданные положениям. При решении задачи синтеза таких механизмов по двум или трем заданным положения выходного звена определяются размеры всех звеньев механизма. В различных машинах находят применение рычажные механизмы, при работе которых ведомое звено должно в определенные моменты времени занимать заданные положениям. При решении задачи синтеза таких механизмов по двум или трем заданным положения выходного звена определяются размеры всех звеньев механизма.
 При синтезе рычажных механизмов могут быть применены как графический, так и аналитический методы. Применение аналитического метода с использованием ЭВМ позволяет решать задачу оптимизации параметров по заданным кинематическим или динамическим условиям. При синтезе механизма, как правило, должны удовлетворяться несколько, часто противоречивых, условий, связанных с назначением механизма, технологией изготовления его деталей и узлов, его эксплуатацией и т.д. Обычно из всех условий выбирают одно основное, а все остальные считаются дополнительными. Основное условие математически выражают в виде целевой функции, экстремум которой определяет искомые параметры синтеза. Дополнительные условия синтеза устанавливают допустимые области существования параметров, т.е. ограничения на эти параметры. При синтезе рычажных механизмов могут быть применены как графический, так и аналитический методы. Применение аналитического метода с использованием ЭВМ позволяет решать задачу оптимизации параметров по заданным кинематическим или динамическим условиям. При синтезе механизма, как правило, должны удовлетворяться несколько, часто противоречивых, условий, связанных с назначением механизма, технологией изготовления его деталей и узлов, его эксплуатацией и т.д. Обычно из всех условий выбирают одно основное, а все остальные считаются дополнительными. Основное условие математически выражают в виде целевой функции, экстремум которой определяет искомые параметры синтеза. Дополнительные условия синтеза устанавливают допустимые области существования параметров, т.е. ограничения на эти параметры.
 Важным параметром для силовых рычажных механизмов, характеризующим условия передачи сил и работоспособность механизма, является угол давления, который во всех положениях механизма не должен превышать некоторое допустимое значение. Условие ограничения угла давления и принимают часто как основное условие при синтезе механизма. Важным параметром для силовых рычажных механизмов, характеризующим условия передачи сил и работоспособность механизма, является угол давления, который во всех положениях механизма не должен превышать некоторое допустимое значение. Условие ограничения угла давления и принимают часто как основное условие при синтезе механизма.

Рисунок 1 – Схема рычажного механизма в 3-х положениях.
 Рассмотрим задачу синтеза плоского шарнирного кривошипно-коромыслового механизма, предназначенного для резки пруткового материала. Схема механизма в двух крайних и одном произвольном положениях изображена на рисунке 1. Рассмотрим задачу синтеза плоского шарнирного кривошипно-коромыслового механизма, предназначенного для резки пруткового материала. Схема механизма в двух крайних и одном произвольном положениях изображена на рисунке 1.
 крайних и одном произвольном положениях изображена на рисунке 1. Ведущее звено – кривошип ОА через шатун АВ приводит в движении коромысло BCD. На последнем располагается верхний нож CD, а нижний неподвижен, т.е. закреплен на стойке. Задача синтеза этого механизма заключается в определении размеров звеньев, при которых будут обеспечены два крайних положения коромысла BCD при непрерывном вращательном движении кривошипа. Крайние положения механизма на рисунке 1 обозначены A0B0CD0 и AKBKCDK. Угол наклона коромысла BC в крайнем нижнем положении ножа обозначены β0, а угол размаха коромысла – βmax. Длину рычага BC обозначим “b”, межосевое расстояние OC – “a”, длину шатуна – “l”, радиус кривошипа – “r”. крайних и одном произвольном положениях изображена на рисунке 1. Ведущее звено – кривошип ОА через шатун АВ приводит в движении коромысло BCD. На последнем располагается верхний нож CD, а нижний неподвижен, т.е. закреплен на стойке. Задача синтеза этого механизма заключается в определении размеров звеньев, при которых будут обеспечены два крайних положения коромысла BCD при непрерывном вращательном движении кривошипа. Крайние положения механизма на рисунке 1 обозначены A0B0CD0 и AKBKCDK. Угол наклона коромысла BC в крайнем нижнем положении ножа обозначены β0, а угол размаха коромысла – βmax. Длину рычага BC обозначим “b”, межосевое расстояние OC – “a”, длину шатуна – “l”, радиус кривошипа – “r”.
 Тогда имеем: Тогда имеем:
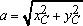 (1) (1)
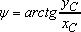 (2) (2)
 Координаты точки B в крайних положениях: Координаты точки B в крайних положениях:
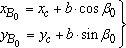 (3) (3)
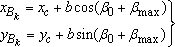 (4) (4)
 Используя выражения (3) и (4), определяем длины отрезков: Используя выражения (3) и (4), определяем длины отрезков: 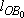 и и 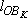 : :
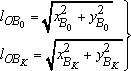 (5) (5)
 Так как Так как 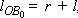 , и , и  , то, используя выражения (5), определяем длины кривошипа и шатуна: , то, используя выражения (5), определяем длины кривошипа и шатуна:
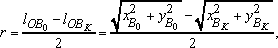 (6) (6)
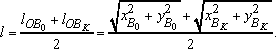 (7) (7)
 Зная координаты точек B0 и BK – уравнения (3) и (4), можно определить углы φ0 и φK, которые характеризуют положения кривошипа при крайних положениях коромысла и определяют коэффициент изменения средней скорости выходного звена: Зная координаты точек B0 и BK – уравнения (3) и (4), можно определить углы φ0 и φK, которые характеризуют положения кривошипа при крайних положениях коромысла и определяют коэффициент изменения средней скорости выходного звена:
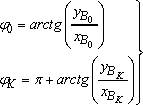 (8) (8)
 На основе этого алгоритма, составлена программа на ЭВМ, позволяющая вычислить параметры синтеза, т.е. r, l, φ0 и φK при заданном положении точки крепления коромысла, т.е. xc и yc, длине коромысла “b” и углах β0 и βmax. Эти исходные данные устанавливают в зависимости от требуемых габаритов механизма и условий компоновки и эксплуатации машины. Варьируя исходные данные, можно с помощью программы получить множество возможных значений параметров синтеза, из которых затем выбрать оптимальный вариант по основному условию, каковым может быть, как отмечалось выше, допустимым угол давления. На основе этого алгоритма, составлена программа на ЭВМ, позволяющая вычислить параметры синтеза, т.е. r, l, φ0 и φK при заданном положении точки крепления коромысла, т.е. xc и yc, длине коромысла “b” и углах β0 и βmax. Эти исходные данные устанавливают в зависимости от требуемых габаритов механизма и условий компоновки и эксплуатации машины. Варьируя исходные данные, можно с помощью программы получить множество возможных значений параметров синтеза, из которых затем выбрать оптимальный вариант по основному условию, каковым может быть, как отмечалось выше, допустимым угол давления.
 Угол давления определятся на схеме механизма в зависимости от того, какое звено является ведущим. Если ведущим является кривошип 1, то сила F1-2 передается на коромысло под углом давления α1-2. Этот угол два раза за цикл (в крайних положениях механизма) достигает максимального значения, равного 90°. Эти положения кривошип проходит благодаря инерции вращающейся массы кривошипа 1. Поэтому при проектировании таких механизмов условие незаклинивания и, следовательно, работоспособность механизма принято оценивать по максимальному углу давления α3-2. При инженерных расчетах считают, что сила F3-2 действует вдоль шатуна AB, тогда угол давления α3-2 – есть угол между шатуном AB и направлением вектора скорости точки В. Угол, дополняющий угол давления до 90°, называется углом передачи движения γ. Это угол между направлением абсолютной скорости точки В - VB и относительной скорости точки В вокруг точки А - VB-A (рис. 1) Угол давления определятся на схеме механизма в зависимости от того, какое звено является ведущим. Если ведущим является кривошип 1, то сила F1-2 передается на коромысло под углом давления α1-2. Этот угол два раза за цикл (в крайних положениях механизма) достигает максимального значения, равного 90°. Эти положения кривошип проходит благодаря инерции вращающейся массы кривошипа 1. Поэтому при проектировании таких механизмов условие незаклинивания и, следовательно, работоспособность механизма принято оценивать по максимальному углу давления α3-2. При инженерных расчетах считают, что сила F3-2 действует вдоль шатуна AB, тогда угол давления α3-2 – есть угол между шатуном AB и направлением вектора скорости точки В. Угол, дополняющий угол давления до 90°, называется углом передачи движения γ. Это угол между направлением абсолютной скорости точки В - VB и относительной скорости точки В вокруг точки А - VB-A (рис. 1)
 Углы давления и передачи движения достигают экстремальных значений в положениях, когда центр шарнира А расположен на линии центров ОС. Для упрощения задачи синтеза и выбора оптимальных параметров механизма с учетом угла давления считают, что экстремума углы передачи движения достигают в крайних положения механизма, т.е. в точках B0 и BK. Тогда условие незаклинивания механизма имеет вид: γmin ≥ γдmin , где γдmin - минимально допустимый, назначаемый при синтезе механизма, угол передачи движения, значение которого зависит от действующих в механизме сил, условий работы механизма и обычно принимается в пределах 30° ÷ 60°. Углы давления и передачи движения достигают экстремальных значений в положениях, когда центр шарнира А расположен на линии центров ОС. Для упрощения задачи синтеза и выбора оптимальных параметров механизма с учетом угла давления считают, что экстремума углы передачи движения достигают в крайних положения механизма, т.е. в точках B0 и BK. Тогда условие незаклинивания механизма имеет вид: γmin ≥ γдmin , где γдmin - минимально допустимый, назначаемый при синтезе механизма, угол передачи движения, значение которого зависит от действующих в механизме сил, условий работы механизма и обычно принимается в пределах 30° ÷ 60°.
 Значение γmin определяется из треугольника OB0C (рис.1): Значение γmin определяется из треугольника OB0C (рис.1):
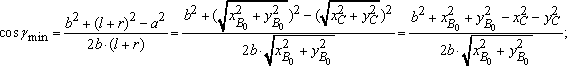 (9) (9)
 В качестве примера рассмотрено решение задачи синтеза механизма силового резания пруткового материала для такого диапазона значений исходных данных: xC=0,45…0,60 м, yC=0…0,15 м, b=0,30…0,40 м, β0=45°…75°, βmax=45°…60°. В качестве примера рассмотрено решение задачи синтеза механизма силового резания пруткового материала для такого диапазона значений исходных данных: xC=0,45…0,60 м, yC=0…0,15 м, b=0,30…0,40 м, β0=45°…75°, βmax=45°…60°.
 Для анализа полученных результатов в таблице 1 приведены некоторые значения входных и выходных параметров, полученные при реализации программы из расчета по приведенному выше алгоритму. Для анализа полученных результатов в таблице 1 приведены некоторые значения входных и выходных параметров, полученные при реализации программы из расчета по приведенному выше алгоритму.
Таблица 1 – Значения параметров синтеза рычажного механизма.
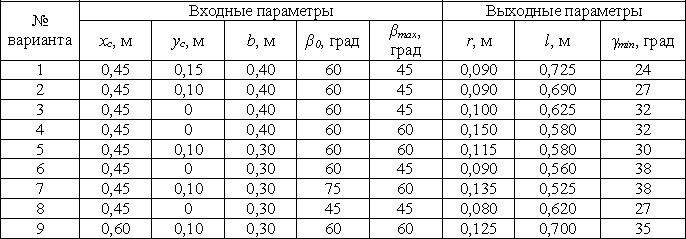
 Анализ данных, приведенных в таблице 1, позволяет сделать следующие выводы. Анализ данных, приведенных в таблице 1, позволяет сделать следующие выводы.
- Увеличение угла ψ (координаты yC) приводит к уменьшению минимального угла передачи движения γmin (варианты 1, 2 и 3).
- Увеличение угла качания коромысла βmax не изменяет минимальный угол передачи движения γmin, а приводит к увеличению радиуса кривошипа r (варианты 3 и 4).
- Увеличение длины коромысла “b” приводит к уменьшению минимального угла передачи движения (варианты 3 и 6).
- С увеличением угла β0 (см. рис. 1) увеличивается угол передачи движения γmin и радиуса кривошипа r (варианты 5, 7 и 8).
- С увеличением межосевого расстояния (координаты xC) угол γmin также увеличивается (варианты 5 и 9).
 Рассмотренная методика синтеза рычажного механизма позволяет из полученных вариантов выбрать оптимальный по заданным условиям работы механизма. Рассмотренная методика синтеза рычажного механизма позволяет из полученных вариантов выбрать оптимальный по заданным условиям работы механизма.
Литература
 1. Теория механизмов и машин: Учеб. для вузов/ К.В.Фролов, С.А.Попов, А.К.Мусатов и др.; Под ред. К.В.Фролова. – М.: Высш. шк., 1987. – 496 с. 1. Теория механизмов и машин: Учеб. для вузов/ К.В.Фролов, С.А.Попов, А.К.Мусатов и др.; Под ред. К.В.Фролова. – М.: Высш. шк., 1987. – 496 с.
|





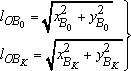 (5)
(5)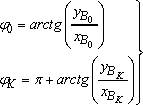 (8)
(8)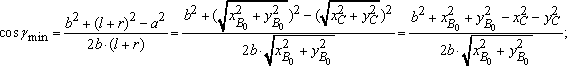 (9)
(9)
