Вступ
Перетворення Фур'є використовується в баготьох галузях науки – в фізиці, теоріЇ чисел, комбинаториці, обробці сигналів, теорії ймовірності, статистиці, криптографції, акустиці, океанології, оптиці, геометрії, та багатьох інших. При обробці сигналів різної природи перетворення Фур'є звичайно розглядається як трансформація сигналу з часової ділянки в частотну.
Дискретне перетворення Фур'є грає важливу роль при аналізі, синтезі та розробці систем та алгоритмів цифрової обробки сигналів. Одна з причин того, що анализ Фур'є грає таку важливу роль в цифровій обрабці сигналів, полягає в існуванні ефективних алгоритмів дискретного перетворення Фур'є.
Ці перетворення зворотні, при чому зворотнє перетворення має практично таку ж саму форму, що й пряме перетворення.
Швидке перетворення Фур'є застосовується в багатьох галузях: радіолокации, стисненні відео та зображень, геології. Багато з цих задач вимагають виконання перетворень в реальному часі, з мінімальною часовою затримкою обчислень.
Для зменшення часу, необхідного для виконання перетворень, можливо розпаралелювання задачі, виконання її на паралельній обчислювальній системі.
Мета цієї дослідницької роботи – вивчення алгоритмів швидкого перетворення Фур'є двовимірних сигналів, подальша розробка програмного забезпечення, що працює на паралельній обчислювальній системі, що виконую обчислювання в реальному часі.
Завдання цієї роботи:
- вивчення різних алгоритмів дискретного двовимірного швидкого перетворення Фур'є;
- вивчення існуючих паралельних обчислювальних систем;
- проектування та написання програмних продуктів, що виконують швидке перетворення Фур'є для великих зображень в реальному часі.
Актуальність
В даний час над цією проблемою працюють багото вчених, таких як Брандон Блойд, Юрій Доценко, Бартон Сміт, Джон Манферделлі та інші. Ця тема актуальна, у зв'язку з широким застосуванням перетворення Фур'є в різних сферах науки. З розвитком комп'ютерної техніки у цієї задачі з'являється все більше і більше ефективних віріантів реалізації на практиці.
Новизна
У теперешній час існує багато методів та алгоритмів ШПФ, які реалізовані як у вигляді спеціальних пакетів, так і в таких стандартних потужних математичних пакетах, як Matlab, Mathcad та Mathematica.
Але за достатньо великих об'ємів обчисленнь вони можуть не надавати необхідної швидкості виконання перетворень, хоч і є ідеальним засобом перевірки вірності отриманих результатів.
Новизна цієї роботи полягає в реалізації дискретного двовимірного швидкого перетворення Фур'є для великих зображень в реальному часі, орієнтуючись на те, щоб отримані результати можна було використовувати для подальшої обробки, без відчутної часової затримки.
Плануємі практичні результати
В результаті виконання роботы, планується отримати програмний продукт, що дозволяє виконувати двовимірні швидкі перетворення Фур'є для зображень великих розмірів, таких як знімки з супутника (100000 на 100000 пікселів) в реальному часі.
Існує два варіанти для вирішення цієї проблеми – пошук найкращих алгоритмів, що покращують швидкість дії системи, та зменшують кількість виконуваємих операцій, та використання спеціальної апаратури, з великими можливостями, такої як паралельна обчислювальна система.
Існує велика кількість ефективних алгоритмів швидкого перетворення Фур'є, та вибір найбільш оптимального з них залежить від апаратних аппаратных засобів.
Серед існуючих паралельних обчислювальних систем треба виділити кластер, та графічні процесори. Планується визначення ефективності для вирішення цієї задачі на кожній з цих ситем. Але варто відзначити, що кластер є значно більш дорогою системою, ніж графічний процесор (в цій роботі розглядаються графічні процесори NVIDIA з підтримкою технології CUDA), та при не значній різниці у часі обчисленнь та обмежених матеріальних коштах більш прийнятним буде вибір другої паралельної обчислювальної системи.
Практичне рішення задачі полягає в знаходженні золотої середини між ціми двома варіантами, що дозволить за еффективного алгоритма рішення задачі та відповідних апаратних засобів отримати оптимальні практичні результати.
Огляд досліджень
У світі існує велика кількість розробок, пов'язаних з алгоритмами ШПФ, що реализовані на різних архітектурах. Серед них можна відзначити такі архітектури:
- кластер;
- графічні процесори;
- Cell процесори.
Серед великої кількості досліджень слід особливо відзначити розробки співробітників корпорації Microsoft Нага К., Говидараю, Брандона Ллойда, Юрия Доценко, Бартона Смита, та Джона Манферделли, а також Василія Волкова. В своїй статті «Високопродуктивні дискретні перетворення Фур'є на графічних процесорах»[1] вони привели наступний аналіз існуючих світових досліджень в галузі швидких перетворень Фур'є та паралельних обчислювальних систем:
«Соренсен та Баррус зкомпілювали базу даних з більш ніж 34000 алгоритмами эфективних ШПФ[2]. Книга Ван Лоана[3] забезпечує розуміння багатьох варіацій алгоритма ШПФ за допомогою матричної структури. Книга також розглядає багато з важливих проблем реалізації. Дослідження, ближче всього пов'язані з темою даної роботи пропонують прискорення обчислення ШПФ, використовуючи відповідну апаратуру, такую як графичні або Cell процесоры. Більшість реалізацій ШПФ на графичних процесорах використовують графічне API, таке як поточна версія OpenGL або DirectX[4],[5][6],[7],[8],[9]. Тим не менше, це API не підтримує прямо розсіювання, доступ до поділювальної пам'яті, або добре подрібнену синхронізацію, доступну на сучасних графічних процесорах. Доступ до цих характеристик зараз надається тільки специфічними API. Бібліотека компаніх NVIDIA для обчислення ШПФ CUFFT[10], використовує CUDA API[11] для досягнення більш високої продуктивності, ніж це можливо з графічними API. Конкуруюча робота Волкова та Казіана[12] також обговорює застосування CUDA.Декілька розробок розглядають використання БПФ на процессорах Cell [13],[14],[15],[16],[17]».[1]
Також Василій Волков розробив та реалізовал алгоритм швидкого перетворення Фур'є, що використовується у стантній бібліотеці NVIDIA CUFFT, а також подав його вдосконалений варіант.
В Україні дослідженнями цієї теми займались:
- кандидат технічних наук Троянский А.В. в десертації «Поточні процесори швидкого перетворення Фур'є з архітектурою, що перебудовувається, на однотипових СБИС»[18];
- кандидат технічних наук Гюрджян М.К. в дисертації по теми «Деякі питання організації паралельних обчислень в багатопроцесорних обчислювальних системах кластерного типа»[19];
- кандидат технічних наук Потопальский В.В. в роботі «Оцінка якості перетворення Фур'є в радіотехнічних та телевізійних системах»[20];
- кандидат технічних наук Керекеша П.В. в дисертации по темі «Комбінований метод перетворення Фур'є та сполучення аналітичних функцій в задачах теорії пружності»[21].
Серед викладачів та студентів Донецького національного техніченого университету схожі задачи досліджує моя однокурсница Смоляна Д.В. в роботі магістра «Дослідження ефективності паралельної реалізації швидкого перетворення Фур'є для цифрових зображень».
Тема швидких перетворень Фур'є порушена також у наступних роботах:
- магістр Алтухов С.В. «Методи перетворення сигналів вхідними ланцюгами системи виброакустической діагностики»;
- магистр Синельников В.Б. «Розробка та дослідження методу оцінювання поточних спектрів радіочастотних сигналів у застосуванні до задачі відновлення їх інформаційних параметрів»;
- магістр Хоменко В.Н. «Розробка типових моделей електромеханічних систем для аналізу можливих аварійних ситуацій в елементах промислових установок»;
- магістр Горелкин А.В. «Дослідження та обгрунтування структури та параметрів мікропроцессорного пристрою контролю вібрації шахтних насосних установок»;
- магістр Нафтулин И.В. «Спектральний аналіз струмів статора асінхроних двигунів з короткозамкненим ротором»;
- магістр Выростков М.А. « Досліджування і розробка алгоритмів і мікропроцесорних структур цифрової обробки сигналів від шахтної системи сигналізації концентрації метана»;
- магістр Коков А.А. «Розробка експертної системи визначення біологічного стану кліток, побудованої на ентропійних методах».
Перетворення Фур'є
Перетворення Фур'є — операція, що зіставляє функції дійсної перемінной іншу функцію дійсної перемінної. Ця нова функція описує коефіцієнти (амплітуди та фази) при розложенні входної функции на елементарні складники – гармонічні коливання з різними частотами.
Дискретне перетворення Фур'є
Дискретним перетворенням Фур'є (ДПФ) над вхідною послідовністю чисел
{x0, x1, …, xn-1},
потужністю n є N, n>1, де xi є Z, i = (0, n-1), назвається таке перетворення, в результате якого утворюється послідовніть
{x-0, x-1, …, x-n-1}
комплексних чисел xk тієї ж потужності, кожний элемент якої розраховується за наступним правилом:

Рисунок 1 - Формула для обчислення ДПФ
де k = (0, n-1), W = e^(-j*Pi/n), где j – мнима одиниця.[2]
Швидкі перетворення Фур'є
Алгоритм швидкого перетворення Фур'є (ШПФ) - це оптимізований за швидкістю спосіб обчислення ДПФ. Основна ідея полягає в наступному:
- необхідно розділити суму (див. рис.1) з N доданків на дві суми по N/2 доданків, та обчислити їх окремо. Для обчислення кожної з підсум, необхідно їх теж розділити на дві суми і т.д.;
- необхідно повторно використовувати вже обчислені доданки.
Використовують або «проріджування по часу» (коли до першої суми потрапляють доданки з парними номерами, а до другої - з непарними), або «проріджування по частоті» (коли до першої суми потрапляють перші N/2 доданків, а до другої - інші). Обидва варіанти рівноцінні. Через специфіку алгоритма доводиться застосовувать тільки N, що є ступенями 2. В цій роботі розглянут випадок з проріджуванням по часу.
В основі алгоритму ШПФ є наступні формули:

Рисунок 2 - Формули алгоритму ШПФ
Тепер розглянемо реалізацію ШПФ. Маємо N=2^T елементів послідовності x{N} та треба отримати послідовність X{N}. Перш за все, доведеться розділити x{N} на дві послідовності: парні та непарні елементи. Потім так само зробити з кожною послідовність. Цей ітераційний процес зупиниться, коли залишаться послідовності довжиною по 2 елементи. Приклад процесу для N=16 показан на рисунку 3.

Рисунок 3 – Перестановка елементів множини x
Усього виконується (log2(N))-1 ітераций.
Розглянемо двійкове подання номерів елементів та місць, що вони займають. Елемент з номером 0 (двійкове 0000) після усіх переміщень займає позицію 0 (0000), елемент 8 (1000) - позицію 1 (0001), елемент 4 (0100) - позицію 2 (0010), елемент 12 (1100) - позицію 3 (0011). І так далі. Не важко помітити зв'язок між двійковим поданням позиції до перемещення та після всіх перестановок: вони дзеркально симетричні. Двійкове подання кінцевої позиції отримується з двійкового подання початкової позиції перестановкою бітов в зворотному порядку. І навпаки[3].
Цей факт не є випадковістю для конкретного N=16, а є закономірністю. На першому кроці парні елементи з номером n перемістились в позицію n/2, а непарні з позиції в позицию N/2+(n-1)/2. Де n=0,1,…,N-1.
На рисунку 4 проілюстрований другий етап обчислення ДПФ

Рисунок 4 – Другий крок обчислення ШПФ
(5 кадрів, 276х204 пікселей, 10 повторень, затримка 1c)
Лініями зверху до низу вказано використання елементів для обчислення значень нових элементів. Дуже зручно те, що два елемента на певних позиціях в массиві дають два елементи на тіх самих місцях. Але належати вони вже будуть іншим, більш довгим масивам, що розміщені на місці колишніх, більш коротких. Це дозволяє обходитись одним масивом даних для входних даних, результатів та зберігання проміжних результатів для всіх T ітерацій.[2]
Двовимірнє дискретне перетворення Фурьє
Двовимірнє дискретне перетворення Фурьє – це дискретне перетворення Фур'є над матрицею, яке обчислюють по формулі:

Рисунок 5 - Формула дискретного двовимірного перетворення Фур'є
де k, i = (0, n-1), l, j = (0, m-1), тобто це є послідовне одномірне ДПФ спочатку над строками, а потім над стовбцями.[2]
Сутність технології NVIDIA CUDA
CUDA (Compute Unified Device Architecture) - це технологія від компанії NVidia, призначена для розробки прикладних програм для масивно-паралельних обчислювальних пристроїв (в першу чергу для GPU починаючи с серії G80).
Технологія CUDA працює на видеокартах NVIDIA починаючи з 8400GS та вище. Різні відеокарти мають різні можливості. Взагалі, якщо в відеокарті наприклад 128 SP(Streaming Processor) — це означає, що там 8 SIMD MP (multiprocessor), кожен з яких робить одночасно 16 операций.
При використанні GPU розробнику доступно декілька видів пам'яті: регістри, локальна, глобальна, поділювальна, константна та текстурна пам'ять. Кожна з цих типів пам'яти має певне призначення, яке обумовлюється її технічними параметрами (швидкість роботи, рівень доступу на читання та запис). Іерархія типів пам'яти представлена на рисунку 6.
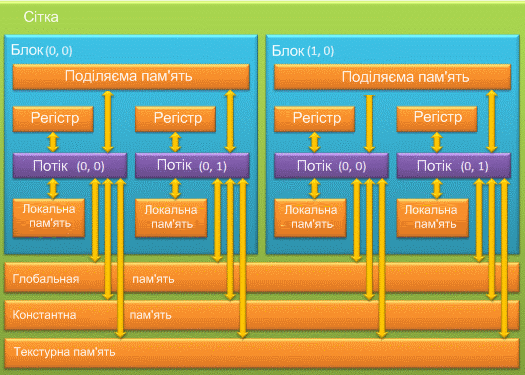 ,
,
Рисунок 6 - Типи пам'яти відеокарти
- Регістрова пам'ять (register) є найшвидшою зі всіх видів. Визначити кількість регістрів доступних GPU можна з допомогою функції cudagetdeviceproperties. Розрахувати кількість регістрів, доступних одній нитці GPU, так само не складає труднощів, для цього необхідно розділити загальне число регістрів на добуток кількості ниток в блоці і кількості блоків в сітці. Всі регістри GPU 32 розрядні. У CUDA немає явних способів використання регістрової пам'яті, всю роботу по розміщенню даних в регістрах бере на себе компілятор;
- Локальная пам'ять (local memory) може бути використана компілятором при великій кількості локальних змінних в якій-небудь функції. По швидкісних характеристиках локальна пам'ять значно повільніша, ніж регістрова. У документації від NVIDIA рекомендується використовувати локальну пам'ять лише в найнеобхідніших випадках. Явних засобів, що дозволяють блокувати використання локальної пам'яті, не передбачено, тому при падінні продуктивності варто ретельно проаналізувати код і виключити зайві локальні змінні;
- Глобальна пам'ять (global memory) – найповільніший тип пам'яті, з доступних GPU. Глобальні змінні можна виділити за допомогою специфікатора __global__, а так само динамічно, за допомогою функцій з сімейства cudmallocxxx. Глобальна пам'ять в основному служить для зберігання великих об'ємів даних, що поступили на device з host’а, дане переміщення здійснюється з використанням функцій cudamemcpyxxx. У алгоритмах, що вимагають високої продуктивності, кількість операцій з глобальною пам'яттю необхідно звести до мінімуму;
- Поділяєма пам'ять (shared memory) - відноситmся до швидкого типа пам'яті. Пам'ять, що розділяється, рекомендується використовувати для мінімізації звернення до глобальної пам'яті, а так само для зберігання локальних змінних функцій. Адресація пам'яті, що розділяється, між нитками потоку однакова в межах одного блоку, що може бути використане для обміну даними між потоками в межах одного блоку. Для розміщення даних в пам'яті, що розділяється, використовується специфікатор __shared__;
- Константна пам'ять (constant memory) - є досить швидкою з доступних GPU. Відмітною особливістю константної пам'яті є можливість запису даних з хоста, але при цьому в межах GPU можливо лише читання з цієї пам'яті, що і обусловлює її назва. Для розміщення даних в константній пам'яті передбачений специфікатор __constant__. Якщо необхідно використовувати масив в константній пам'яті, то його розмір необхідно вказати заздалегідь, оскільки динамічне виділення на відміну від глобальної пам'яті в константній не підтримується. Для запису з хоста в константну пам'ять використовується функція cudamemcpytosymbol, і для копіювання з device’а на хост cudamemcpyfromsymbol, як видно цей підхід дещо відрізняється від підходу при роботі з глобальною пам'яттю;
- Текстурна пам'ять (texture memory) - як і виходить з назви, призначена головним чином для роботи з текстурами. Пам'ять текстури має специфічні особливості в адресації, читанні і записі даних.
Основними плюсами CUDA є її безкоштовність, простота (програмування ведеться на «розширеному С») і гнучкість.
Можливе поліпшення продуктивності шляхом підключення відразу декількох відеокарт. [23]
Якщо відеокарта підключена до монітору, то обчислення продовжуватимуться лише 5 секунд, а потім всі значення обнуляються. Вирішенням даної проблеми є відключення драйвера, або використання графічного процесора лише для обчислень.
Використання NVIDIA CUDA для обчислення швидких перетворень Фур'є
Для обчислення швидких перетворень Фур'є в технології CUDA існує стандартна бібліотека CUFFT. Недоліком цієї бібліотеки є обмеження на розмір швидкого перетворення. Так само арифметика чисел з подвійною точністю підтримується лише в останніх версіях бібліотеки.
CUDA варіант FFT підтримує 1d, 2d, і 3d перетворення комплексних і дійсних даних, пакетного виконання для декількох 1d трансформацій в паралелі, розміри 2d і 3d трансформацій можуть бути в межах [2, 16384], для 1d підтримується розмір до 8 мільйонів елементів.
Також можливо зменшення часу обчислень.
Цьому, необхідна розробка власного алгоритму обчислення, ефективного для великих розмірів перетворень, і що підтримує арифметику чисел з подвійною точністю.
Приклади алгоритмів обчислення і їх результативність наведені в статті «Високопродуктивні дискретні перетворення Фур'є на графічних процесорах».
Результати
На даний момент, вивчені основні алгоритми обчислення дискретного двовимірного швидкого перетворення Фур'є. Так само розглянуті вже існуючі дослідження по даній темі, вивчені найбільш ефективні і корисні з них для подальшого розвитку і вживання, особлива увага приділена алгоритмам з розпаралелюванням обчислень.
Була написана програма, що обчислює двовимірне швидке перетворення Фур'є для зображень. Час обчислень для входних даних різних розмірів для вхідних даних різних розмірів при тестуванні програми на персональному комп'ютері приведені в таблиці 1.
Таблиця 1 - Час виконання двовимірного швидкого перетворення Фур'є
| Висота | Ширина | Час виконання |
| 4 | 4 | 0,0468 c |
| 8 | 8 | 0,0625 c |
| 16 | 16 | 0,0937 c |
| 64 | 64 | 0,3437 c |
| 512 | 512 | 5,5781 c |
| 1024 | 1024 | 26,8125 c |
| 2048 | 2048 | 1 мин 54,859 с |
Розглянута нова технологія обчислення на графічних процесорах NVIDIA CUDA. Вивчені основні її достоїнства і недоліки. Так само скомпільована і успішно виконана тестова програма на графічному процесорі NVIDIA Geforce 8600 GT.
За місяць планується написання програми, що обчислює двовимірне швидке перетворення Фур'є з використанням технології NVIDIA Cuda.
Заключення
Розглянута архітектура і різноманіття різних алгоритмів швидкого перетворення Фур'є дозволяють виконувати обчислення, значно перевершуючі можливості звичайного персонального комп'ютера. Обчислювальні можливості паралельних обчислювальних систем дозволяють отримати плановані результати для виконання дискретного двовимірного швидкого перетворення Фур'є в реальному часі для великих зображень.
При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2009 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Література
1. Говидараю Н.К., Ллойд Б., Доценко Ю., Смит Б., Манферделли Д. Высокопроизводительные дискретные преобразования Фурье на графических процессорах/ компания Microsoft, - ../library/translate.htm
2. Sorensen H.V., Burrus C. S. Fast Fourier Transform Database.PWS Publishing, 1995.
3. Loan C.V. Computational Frameworks for the Fast Fourier Transform / Society for Industrial Mathematics, 1992.
4. Moreland K., Angel E. The FFT on a GPU / Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Conference on Graphics Hardware, 2003.
5. Spitzer J. Implementing a GPU-efficient FFT / SIGGRAPH Course on Interactive Geometric and Scientific Computations with Graphics Hardware, 2003.
6. Mitchell J.L., Ansari M.Y., Hart E. Advanced image processing with DirectX 9 pixel shaders / ShaderX2: Shader Programming Tips and Tricks with DirectX 9.0, W. Engel, Ed. Wordware Publishing, Inc.,2003.
7. Jansen T., B. Rymon-Lipinski B., Hanssen N., Keeve E. Fourier volume rendering on the GPU using a split-stream-FFT / Proceedings of the Vision, Modeling, and Visualization Conference 2004.
8. Sumanaweera T., Liu D. Medical image reconstruction with the FFT / GPU Gems 2, Pharr M., Ed. Addison-Wesley, 2005.
9. Govindaraju N.K, Larsen S., Gray J., Manocha D. A memory model for scientific algorithms on graphics processors / Supercomputing 2006.
10. CUDA CUFFT Library/ Официальный сайт разработчика, - http://developer.download.nvidia.com/compute/cuda/2_1/toolkit/docs/CUFFT_Library_2.1.pdf
11. NVIDIA CUDA: Compute Unified Device Architecture / NVIDIA Corp., 2007.
12. Volkov V., Kazian B. Fitting FFT onto the G80 architecture / компания Microsoft, - http:www.cs.berkeley.edu/kubitron/courses/cs258-S08/projects/reports/project6 report.pdf
13. Chow A.C., Fossum G.C, Brokenshire D.A. A programming example: Large FFT on the cell broadband engine / Whitepaper, 2005.
14. Cico L., Cooper R., Greene J. Performance and programmability of the IBM/Sony/Toshiba Cell broadband engine processor / Whitepaper, 2006.
15. Williams S., Shalf J., Oliker L., Kamil S., Husbands P., Yelick K. The potential of the cell processor for scientific computing / CF 06:Proceedings of the 3rd Conference on Computing Frontiers, 2006, pp.9–20.
16. Bader D.A., Agarwal V. FFTC: fastest Fourier transform for the IBM Cell broadband engine / 14th IEEE International Conference on High Performance Computing (HiPC), pp. 172–184, 2007.
17. Frigo M., Johnson S. G. FFTW on the cell processor / компания Microsoft, - http://www.fftw.org/cell/index.html
18. Троянский А.В. Поточные процессоры быстрого преобразования Фурье с перестраиваемой архитектурой на однотипных СБИС: Дис. канд. техн. наук: 05.12.21 / Одесский гос. политехнический ун-т. - О., 1997. - 185с. -
http://www.dissua.com/contua/pk-15757.html
19. Гюрджян М. К. Некоторые вопросы организации параллельных вычислений в многопроцессорных вычислительных системах кластерного типа: дис. канд. техн. наук: 05.13.05 / Институт проблем информатики и автоматизации НАН РА. - Ереван, 2004. -
http://www.dissua.com/contua/pk-20301.html
20. Потопальский В. В. Оценка качества преобразования Фурье в радиотехнических и телевизионных системах : дис.канд.техн.наук: 05.12.17 / АН Украины. — Львов, 1993. — 189с. -
http://www.dissua.com/contua/pk-260506.html
21. Керекеша П.В. Комбинированный метод преобразования Фурье и сопряжения аналитических функций в задачах теории упругости: Дис. д-ра физ.-мат. наук: 01.02.04 / Одесский гос. ун-т им. И.И.Мечникова. - О., 1999. - 314с. -
http://www.dissua.com/contua/pk-11181.html
22. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. Москва, Мир – 1989. 248 с.
23. NVIdiA Cuda Programming Guide / сайт NVIDIA, - http://developer.download.nvidia.com/compute/cuda/2_2/toolkit/docs/NVIDIA_CUDA_Programming_Guide_2.2.pdf
24. Schivea H., Chiena C., Wonga S.,Tsaia Y., Chiueha T. Graphic-Card Cluster for Astrophysics (GraCCA) - Performance Tests / Сборник статей по математике, физике, программированию и др., - http://xxx.lanl.gov/ftp/arxiv/papers/0707/0707.2991.pdf
