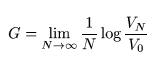
(Extract, pp. 917-920)
Автореферат| Библиотека|Ссылки|Отчет| | Биография |Индивидуальный раздел|
Источник: THE BELL SYSTEM TECHNICAL JOURNAL, JULY 1956,pp. 917-926
http://www.bjmath.com/bjmath/kelly/kelly.pdf
A New Interpretation of Information Rate
If the input symbols to a communication channel represent
the outcomes of a chance event on which bets are available at odds consistent
with their probabilities (i.e., "fair" odds), a gambler can use the knowledge
given him by the received symbols to cause his money to grow exponentially. The
maximum exponential rate of growth of the gambler's capital is equal to the rate
of transmission of information over the channel. This result is generalized to
include the case of arbitrary odds.
Thus we find a situation in which the transmission rate is significant even
though no coding is contemplated. Previously this quantity was given
significance only by a theorem of Shannon's which asserted that, with suitable
encoding, binary digits could be transmitted over the channel at this rate with
an arbitrarily small probability of error.
INTRODUCTION
Shannon defines the rate of transmission over a noisy communication channel in
terms of various probabilities.1 This definition is given significance by a
theorem which asserts that binary digits may be encoded and transmitted over the
channel at this rate with arbitrarily small probability of error. Many workers
in the field of communication theory have felt a desire to attach significance
to the rate of transmission in cases where no coding was contemplated. Some have
even proceeded on the assumption that such a significance did, in fact, exist.
For example, in systems where no coding was desirable or even possible (such as
radar), detectors have been designed by the criterion of maximum transmission
rate or, what is the same thing, minimum equivocation. Without further analysis
such a procedure is unjustified.
The problem then remains of attaching a value measure to a communication system
in which errors are being made at a non-negligible rate, i.e., where optimum
coding is not being used. In its most general formulation this problem seems to
have but one solution. A cost function must be defined on pairs of symbols which
tells how bad it is to receive a certain symbol when a specified signal is
transmitted. Furthermore, this cost function must be such that its expected
value has significance, i.e., a system must be preferable to another if its
average cost is less. The utility theory of Von Neumann2 shows us one way to
obtain such a cost function. Generally this cost function would depend on things
external to the system and not on the probabilities which describe the system,
so that its average value could not be identified with the rate as defined by
Shannon.
The cost function approach is, of course, not limited to studies of
communication systems, but can actually be used to analyze nearly any branch of
human endeavor. The author believes that it is too general to shed any light on
the specific problems of communication theory. The distinguishing feature of a
communication system is that the ultimate receiver (thought of here as a person)
is in a position to profit from any knowledge of the input symbols or even from
a better estimate of their probabilities. A cost function, if it is supposed to
apply to a communication system, must somehow reflect this feature. The point
here is that an arbitrary combination of a statistical transducer (i.e., a
channel) and a cost function does not necessarily constitute a communication
system. In fact (not knowing the exact definition of a communication system on
which the above statements are tacitly based) the author would not know how to
test such an arbitrary combination to see if it were a communication system.
What can be done, however, is to take some real-life situation which seems to
possess the essential features of a communication problem, and to analyze it
without the introduction of an arbitrary cost function. The situation which will
be chosen here is one in which a gambler uses knowledge of the received symbols
of a communication channel in order to make profitable bets on the transmitted
symbols.
THE GAMBLER WITH A PRIVATE WIRE
Let us consider a communication channel which is used to transmit the results of
a chance situation before those results become common knowledge, so that a
gambler may still place bets at the original odds. Consider first the case of a
noiseless binary channel, which might be used, for example, to transmit the
results of a series of baseball games between two equally matched teams. The
gambler could obtain even money bets even though he already knew the result of
each game. The amount of money he could make would depend only on how much he
chose to bet. How much would he bet? Probably all he had since he would win with
certainty. In this case his capital would grow exponentially and after N bets he
would have 2^ times his original bankroll. This exponential growth of capital is
not uncommon in economics. In fact, if the binary digits in the above channel
were arriving at the rate of one per week, the sequence of bets would have the
value of an investment paying 100 per cent interest per week compounded weekly.
We will make use of a quantity G called the exponential rate of growth of the
gambler's capital, where
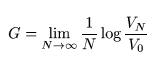
where VN is the gambler's capital after N bets, Vo is his
starting capital, and the logarithm is to the base two. In the above example G =
1.Consider the case now of a noisy binary channel, where each transmitted symbol
has probability, p, of error and q of correct transmission. Now the gambler
could still bet his entire capital each time, and, in fact, this would maximize
the expected value of his capital, {VN), which in this
case would be given by
![]()
This would be little comfort, however, since when N was large he would probably
be broke and, in fact, would be broke with probability one if he continued
indefinitely. Let us, instead, assume that he bets a fraction, Ј, of his capital
each time. Then
![]()
where W and L are the number of wins and losses in the N
bets. Then

Let us maximize G with respect to Ј. The maximum value with respect to the Yi of
a quantity of the form Z = J2^i l°g^b subject to the constraint = Y, is obtained
by putting
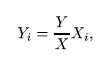
where
![]()
.This may be shown directly from the convexity of the
logarithm.
Thus we put
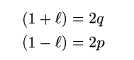
and

which is the rate of transmission as defined by Shannon.
One might still argue that the gambler should bet all his money (make 1=1) in
order to maximize his expected win after N times. It is surely true that if the
game were to be stopped after N bets the answer to this question would depend on
the relative values (to the gambler) of being broke or possessing a fortune. If
we compare the fates of two gamblers, however, playing a nonterminating game,
the one which uses the value I found above will, with probability one,
eventually get ahead and stay ahead of one using any other Ј. At any rate, we
will assume that the gambler will always bet so as to maximize G.