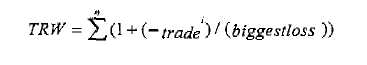
(Extract, pp. 51-61)
Àâòîðåôåðàò| Áèáëèîòåêà|Ññûëêè|Îò÷åò| | Áèîãðàôèÿ |Èíäèâèäóàëüíûé ðàçäåë|
Èñòî÷íèê: SPECIAL REPORT ON MONEY MANAGEMENT. Copyright @ 1997 by I.I.T.M., Inc.
Special Report on Money Management
(Abstract)
Technique I -Get Best Reward-to-Risk Ratio and then Leverage Yourself
Let's say you've developed several systems that together give you an average return of 20% per year with a maximum drawdown of about 4%. If you can achieve that, then you've got a reward-to-risk ratio of 5 to 1. That kind of record is outstanding and few other traders can duplicate it. As a result, the best way for you to produce maximum profits is to simply leverage yourself. For example, if you traded $100,000 as if it were $500,000 in that system, then you'd probably have an annual return of 100% with a maximum drawdown of about 20%. This is much better than simply going for a system that produces the highest rate of return.
Technique 2 -Optimal f and the Kelly Criterion
Ralph Vince has suggested that if "you are not trading for optimal profits, then you belong on a psychiatrist's couch rather than in the markets" 3 Yet, trading for optimal profits also means trading with large drawdowns. For most people, such drawdowns are totally unacceptable. They probably would stop trading at the bottom of the drawdown as a net loser and have no chance of letting the system work. Nevertheless, its possible to make large rates of return by simply adding "optimal" money management to your trading system.
Ralph Vince's solution to optimal money management is to risk an "optimal fixed fraction" or ‘7 of one's largest "historical drawdown." In Vince's word's:
"For any given independent trial situation, which you have an edge (i.e., a positive mathematical expectation), there exists an optimal fixed fraction (fj between 0 and 1 as a divisor of your biggest loss to bet on each and every event to maximize your winnings. Most people think that the optimal fixed fraction is the percentage of your total stake to bet. This is absolutely false. Optimal f is the divisor of our biggest loss, the result of which we divide by our total stake to know how many bets to make or contracts to have on." Portfolio Money Management, p. 80.4
I have two problems with optimal "f’ as a guide for optimal gains'. First, since it is based upon one's largest historical loss, it makes the assumption that you have’ already had your worst loss. It's muchmore useful for the average trader to assume that one's worst loss has never occurred.
Second, the calculations require an iterative mathematical procedure that is quite complex. Vince is a man who has had no college education, but has studied mathematics extensively. This unusual combination has made him very difficult to read, even for someone schooled in mathematics. For example, he'll introduce a rather vague term, like Terminal Wealth Relative, and then simply refer to it as TWR throughout the rest of the book.
Thus, Vince's formula for optimal f amounts to using a computer (and perhaps Vince's own software) to test all possible values between 0.01 and 1.00 increments of Terminal Wealth Relative or TWR. His exact formula is:
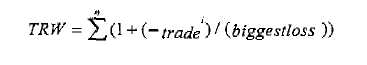
For the reasons suggested, I much prefer the Kelly Criterion for estimating maximum bet size. Vince says that the Kelly Criterion should not apply to trading — it only applies to win-loss type data. However, you can use your past trading (or historical testing) to determine the information you need.
Basically, you need your winning percentage (which we'll call W) and you need the average size of your winning trades divided by the average size of your losing trades (which we'll call R). Thus, the Kelly criterion can be calculated as follows:
Kelly % = W - [(1 - W)/R]
Let's look at how the Kelly Criterion might work. Suppose you have a system that has a winning percentage of 0.5. Your system also has average profits that are twice as large as the size of your average loss. Thus, W = 0.5 and R = 2. Using these numbers results in the following.
Kelly % = 0.5 - [(I - 0.5)/2]
= 0.5 - [0.5/2]
= 0.5-0.25
= 0.25
Thus, the percentage of equity bet that would provide a maximum rate of return is 25%.
However, if you have a system that is right 50% of the time, you can easily be wrong 10 or even 20 times in a row during a large number of trials. Thus, you could never risk 25% of your remaining equity — unless you like the kind of drawdowns show in Table 4 at the 2530% level.
The Kelly Criterion can still be useful for people wanting to go for optimal rates of return. Simply take about 80% of the Kelly Criterion — in this case 80% of 25% is equal to 20%. Figure out how many trades you are likely to have on at one time and then divide your 80%-Kelly value by that number of trades. For example, if you are likely to have on as many as 10 trades at one time, then your optimal risk size would probably be about 2% using this system.
Technique 3 -Playing the "Market's Money"
Perhaps the best way to go for top returns is to distinguish between your starting equity and the market's money. You can't do this with other people's money, because they typically get upset-even when you give back open profits.
Suppose your objective is to achieve a maximum income by some future date. You're willing to do whatever it takes to increase that income as long as you don't lose your starting equity. On that assumption, you can design a special system that risks very little of your starting equity and instead risks the markets money at an optimal level.
As an example, suppose you start January I*’ with $100,000. Your objective is to make as much money as you can by December 31” while risking as little as possible of your starting equity. Here's one way you might do it:
You might begin by risking only 1% of your starting equity, but be willing to use an optimal level (or near optimal level) with the market's money. Let's say that you've determined that your system is optimal risking 20%. However, you've determined that you might have as many as five positions in the market at any one time (and this is the maximum you will have). Consequently, you are willing to risk up to 4% per position at an optimal level.
The real advantage of this system is that, as soon as you move into profits, your ability to make profits goes up dramatically — but so does your risk. Let's say that your first position is in crude oil. You initially risk 1% of your $100,000 or $1.000. By the time, your second trade comes along, you have $3,000 in open profits. You can now risk $1,000 of your original equity plus 4% of your open profits or $120. Thus, you can assume $I,,120 worth of risk on your second trade under this model.
Imagine you've been doing really well with this model. By March, you've accumulated $25,000 in new profits. At this point, you are now risking $1,000 (1% of your starting equity) plus 4% of your $25,000 in new profits or another $1,000. Your risk (Le., your ability to profit) has now doubled even though your equity has only gone up by 25%.
Of course, trading doesn't necessarily bless you by starting out with big profits. You might begin with a losing streak. If you want to be careful about protecting your starting equity, you may want to cut back your risk if you go into a drawdown in your starting equity. For example, you may decide that if you lose 5% of your starting equity (i.e., and get down to 595,000) you'll cut your risk down to 0.9%. If you drop another 5% down to $90,000, you'll cut your trading risk down to 0.8%. Since your trading risk drops down dramatically as you move into your equity, you are not likely to lose much of your starting equity."
Technique 4 -Creative Money Management with the Market's Money
Another equally profitable money management routine allowing you to build your capital quickly amounts to playing the market's money through pyramid money management and stop adjustment. For example, suppose you have a $100,000 account and you want to make your money grow as rapidly as possible, You are using a 3 times volatility stop as I did in the random entry trading system (reference Course Update #23a). You've also decided that your system is optimal risking 24% of equity at a time, using a reduced total equity model. You plan to have as many as six open positions at one time, so you are willing to risk up to 4% per position — but not all at once. You'll build up to a position as big as 4% as your profits increase. Your initial risk will only be 2%.
Let's see how such a money management system might work. You buy corn at $3.025. The ten day average true range (which we'll call "V") is 3.5 cents. Therefore, a 3 times volatility stop is 10.5 cents (i.e., at $2.92) which amounts to a total risk of $525. You can risk 2% of your $100,000, which amounts to 3 contracts (rounded down to the nearest contract).
Your pyramiding scheme is to add one contract every time your profit increases by one daily volatility or V (i.e., which is currently 3.5 cents). When this occurs, (i.e., corn moves to $3.06) you risk another 2% with a 3 times V stop at $2.955. However, your stop on the original position moves up by 3.5 cents to $2.955. Thus, you now have six contracts all with stops at $2,955. However, notice that vour total exposure of your original equity is now only 3% (actually less due to rounding) because you raised your initials too.
Let's say that your daily volatility now increases to 4 cents. Thus, a new stop would now be 12 cents or $600. Corn moves up to $3.10, so you can now risk another 2%. (Actually, you could have done so at 53.095 — when the price had increase by the old V-value of 3.5 cents.) Your reduced total equity is now $97,000 and 2% of that is 51,940. As a result, you can still purchase 3 contracts at $3.gO — with a stop at $2.98. You also get to raise your stop on both of your other units by their respective V-values. Therefore you now have six contracts with stops at $2.99 and three contracts with a stop at $2.98.
You might be saying, "How can you do that? Your risk is over the 3% limit with the reduced total equity model." No, it isn't because you raised your other stops enough so that your exposure is still about 3% of your reduced total equity.
|
Contracts |
Current Stop |
Remaining Risk in Original Equity |
Total Risk to Original Equity |
|
3 at $3,025 |
$2.99 |
3.5 cents |
10.5 cents = $525 |
|
3 at $3.06 |
$2.99 |
7 cents |
21 cents = $1,050 |
|
3 at 33.10 |
$2.98 |
12 cents |
36 cents = $1,800 |
Table 6
Table 6 summarizes your current position. Notice that your total risk to your original $100,000 is now $3,375 (or 3.375%).
Let's say that volatility stays at 4 cants and corn now goes to $3.14. Its time to risk another two percent. Your reduced total equity is now $96,525. You can risk 2% of that or $1932.50. Your 12 cent stop is a 5600 risk, so you can again purchase another 3 contracts. You 'must also raise your stops on the existing contracts. The stop on the first six contracts raises to 53.025 (i.e., it was raised 3.5 cents, the original V). The stop on the last three contracts raises to 53.02.
Consider where you are with respect to the reduced total equity model in terms of risk, You now have risked 2% four times, but have you exceeded your 4% limit?
|
Contracts |
Current Stop |
Remaining Risk in Original Equity |
Total Risk to Original Equity |
|
3 at $3,025 |
$303 |
0 |
|
|
3 at $3,06 |
$3,03 |
3.5 cents |
10,5 cents = $550 |
|
3 at $3.10 |
S3.02 |
8 cents |
24 cents = $1,200 |
|
3 at S3 14 |
S3.02 |
12 cents |
36 cents = $1,800 |
Table 7
The total risk to your original equity is now only $3,550 or 3.55% — still under our 4% limit. So let's say corn starts to really get volatile now and V goes to 6 cents. And you get a chance to buy more corn as it goes up to $3.20 (actually you could buy at $3.18, when it increased by the last value of V). But we'll say that you buy at $3.20.
Your total reduced equity is now $96,450 and 2% of that is $1,929. Your new stop, at 3 V, is now 18 cents or $900. Thus, you can now only purchase two contracts, but you also get to raise your other stops. Let's say that we make a decision to leave the breakeven stop alone, giving it plenty of room to move. However, you can now move the stop on the second 3 contracts purchased to breakeven; move the stop on the contracts purchased at $3.10 to $3.06; and move the stop on the contracts purchased at $3.14 to $3.06. Thus, the current risk picture is shown in Table 8.
Notice that by the reduced total equity model, your risk has changed very little. The risk to your original equity is now $3,600 or 3.6%.
|
Contracts |
Current Stop |
RemalnlngRisk in Original Equity |
Total Risk to Original Equity |
|
|
3 at 33.02? |
$3.03 |
n |
n |
|
|
3 at $3.06 |
$3.06 |
0 |
0 |
|
|
3 at $3.10 |
53.06 |
4 cent5 |
12 cents = $600 |
|
|
3 at 53.14 |
$3.06 |
8 cents |
24 cents = 51,200 |
|
|
7 ui 53 20 |
$3~02 |
18 cents |
36 cents =$1,800 |
|
Table 8
Corn now goes to $3.26, and V remains at 6. As a result, you decide to add another 2% and raise your other stops by their previous V values. Again, you can only buy two more units and their stop is now 53.08. Your portfolio now looks like Table 9.
|
Contracts |
current Stop |
Remaining Risk in Original Equity |
Total Risk to Original Equity |
|
3 at 53.025 |
$3.025 |
0 |
0 |
|
3 at $3.06 |
$3.06 |
0 |
0 |
|
3 at 53.10 |
$3.10 |
0 |
0 |
|
3 at $3.14 |
53.10 |
4 cents |
12 cents = 5600 |
|
2 at 53.20 |
53.08 |
12 cents |
24 cents = $1,200 |
|
7 at s3 7fi |
$3~08 |
1 a C~S |
36 cents = $1.800 |
Table 9
Notice that your original exposure is still just 53600. If the market kept going up, you could continue to add contracts to your portfolio — even if you never raised any of your stops past breakeven — and you would still be unlikely to exceed your 4% risk ceiling per position. However. you do run the risk of a series of limit moves against you. As a result, you must set a physical limit to the total number of times that you are willing to add 2% more risk and increase your stops.
Now let's say the market dropped the next day and gave you a sell signal (i.e., your sell signal is independent of your money management stops). You get out at 53.21. Basically, you'd make 55.5 cents on the first 3 contracts; 45 cents on the next three contracts, 33 cents on the next three contracts, 21 cents on the next three contracts, and 2 cents on the next 2 contracts. You'd lose 10 cents on the last two contracts. Your total profit is $7,325.
Initially, you only risked $1575 on what might have been a false signal, You only added risk as the signal proved itself. Had you invested the 4% initially, you would have purchased 7 contracts at a risk of $3,675. Those 7 contracts would have made you $6,475.
Some of you might be saying "... but you ended up with 16 contracts. It might have been disastrous if you'd had some limit moves against you." That's true. but my point was to show you creative money management. A method very similar to the one described has been used by a number of well-known traders to produce consistent and very large rates of return. Furthermore, you could offset the risk with options which would avoid the risk of a runaway market against you7
There are any number of variables that you can vary in creative money management — your initial stop, your maximum risk per commodity, moving your stops in your favor, your equity model, your money management model, etc.. For example, you could even use the idea of increasing your "reduced total equity" by raising your stop to justify opening up positions in other commodities. This could really help the small trader who does not have a large enough account to trade using most of these models.
Conclusion
My point in writing this report is to get you to think about money management (especially, creative money management) instead of just creative entry techniques. Money management is the most important part of a trading system. Yet for psychological reasons most people avoid thinking about it entirely. These money management variables will have much more of an impact on your bottom line profits (or losses, if misused) than the latest entry signal you've been studying.
Literature
1. Ed Seykota and Dave Drut. Determining Optimal Risk. /Technical Analysis of Stocks and Commodities , March 1993, p. 46-49.
2. Ralph Vince The New Money Management. New York: Wiley, 1995.Page 60
3. Ralph Vince Portfolio Money Management. New York: Wiley, 1995.