FINDING THE OPTIMAL f BY THE GEOMETRIC MEAN

In trading we can count on our wins being for varying amounts and our losses being for varying amounts. Therefore the Kelly formulas could not give us the correct optimal f. How then can we find our optimal f to know how many contracts to have on and have it be mathematically correct?
Here is the solution. To begin with, we must amend our formula for finding HPRs to incorporate f:

(III) HPR = 1 + f * ( -Trade/Biggest loss)

where f = The value we are using for f.
-Trade = The profit or loss on a trade (with the sign reversed so that losses are positive numbers and profits are negative).
Biggest Loss = The P&L that resulted in the biggest loss. (This should always be a negative number.)
And again, TWR is simply the geometric product of the HPRs and geomet¬ric mean (G) is simply the Nth root of the TWR.

 

 

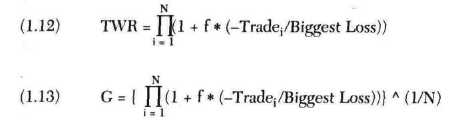
-Tradei = The profit or loss on the ith trade (with the sign
reversed so that losses are positive numbers and profits are negative).
Biggest Loss = The P&L that resulted in the biggest loss. (This should always be a negative number.)
N = The total number of trades.
G = The geometric mean of the HPRs.

By looping through all values forfbetween .01 and 1, we can find that value for f which results in the highest TWR. This is the value for f that would provide us with the maximum return on our money using fixed frac¬tion. We can also state that the optimal f is the f that yields the highest geometric mean. It matters not whether we look for highest TWR or geometric mean, as both are maximized at the same value for f.

Doing this with a computer is easy, since both the TWR curve and the geometric mean curve are smooth with only one peak. You simply loop from f = .01 to f = 1.0 by .01. As soon as you get a TWR that is less than the previous TWR, you know that the f corresponding to the previous TWR is the optimal f. You can employ many other search algorithms to facilitate this process of finding the optimal fin the range of 0 to 1. One of the fastest ways is with the parabolic interpolation search procedure detailed in Portfolio Management Formulas.

TO SUMMARIZE THUS FAR

You have seen that a good system is the one with the highest geometric mean. Yet to find the geometric mean you must know f. You may find this confusing. Here now is a summary and clarification of the process:

1. Take the trade listing of a given market system.
2. Find the optimal f, either by testing various f values from 0 to 1 or through iteration. The optimal f is that which yields the highest TWR.
3. Once you have found f, you can take the Nth root of the TWR that corresponds to your f, where N is the total number of trades. This isyour geometric mean for this market system. You can now use this geometric mean to make apples-to-apples comparisons with other market systems, as well as use the f to know how many contracts to trade for that particular market system.

Once the highestfis found, it can readily be turned into a dollar amount by dividing the biggest loss by the negative optimalf. For example, if our biggest loss is $100 and our optimal f is .25, then -$100/-.25 = $400. In other words, we should bet 1 unit for every $400 we have in our stake.

If you're having trouble with some of these concepts, try thinking in terms of betting in units, not dollars (e.g., one $5 chip or one futures contract or one 100-share unit of stock). The number of dollars you allocate to each unit is calculated by figuring your largest loss divided by the negative optimal f.

The optimal f is a result of the balance between a system's profit-making ability (on a constant 1 -unit basis) and its risk (on a constant 1 -unit basis).

Most people think that the optimal fixed fraction is that percentage of your total stake to bet. This is absolutely false. There is an interim step involved. Optimal f is not in itself the percentage of your total stake to bet, it is the divisor of your biggest loss. The quotient of this division is what you divide your total stake by to know how many bets to make or contracts to have on.

You will also notice that margin has nothing whatsoever to do with what is the mathematically optimal number ofcontracts to have on. Margin doesn't matter because the sizes of individual profits and losses are not the product of the amount of money put up as margin (they would be the same whatever the size of the margin). Rather, the profits and losses are the prod¬uct of the exposure of 1 unit (I futures contract). The amount put up as margin is further made: meaningless in a money-management sense, because the size of the loss is not limited to the margin.

Most people incorrectly believe that f is a straight-line function rising up and to the right. They believe this because they think it would mean that the more you are willing to risk the more you stand to make. People reason this way because they think that a positive mathematical expectancy is just the mirror image of a negative expectancy. They mistakenly believe that if increasing your total action in a negative expectancy game results in losing faster, then increasing your total action in a positive expectancy game will result in winning faster. This is not true. At some point in a positive expectancy situation, further increasing your total action works against you. That point is a function of both the system's profitability and its consistency (i.e., its geometric mean), since you are reinvesting the returns back into the system.

It is a mathematical fact that when two people face the same sequence of favorable betting or trading opportunities, if one uses the optimal f and the other uses any different money-management system, then the ratio of the optimal f bettor's stake to the other person's stake will increase as time goes on, with higher and higher probability. In the long run, the optimal f bettor will have infinitely greater wealth than any other money-management sys¬tem bettor with a probability approaching 1. Furthermore, if a bettor has the goal of reaching a specified fortune and is facing a series of favorable betting or trading opportunities, the expected time to reach the fortune will be lower (faster) with optimal f than with any other betting system.

Let's go back and reconsider the following sequence of bets (trades):
+9, +18, +7, +1, +10,-5,-3,-17,-7
Recall that we determined earlier in this chapter that the Kelly formula was not applicable to this sequence, because the wins were not all for the same amount and neither were the losses. We also decided to average the wins and average the losses and take these averages as our values into the Kelly formula (as many traders mistakenly do). Doing this we arrived at an f value of .16. It was stated that this is an incorrect application of Kelly, that it would not yield the optimal f. The Kelly formula must be specific to a single bet. You cannot average your wins and losses from trading and obtain the true optimal fusing the Kelly formula.
Our highest TWR on this sequence of bets (trades) is obtained at .24, or betting $1 for every $71 in our stake. That is the optimal geometric growth you can squeeze out of this sequence of bets (trades) trading fixed fraction. Let's look at the TWRs at different points along 100 loops through this sequence of bets. At 1 loop through (9 bets or trades), the TWR for f = .16 is 1.085, and for f = .24 it is 1.096. This means that for 1 pass through this sequence of bets an f = .16 made 99% of what an f = .24 would have made.