Новое в динамическом управлении капиталом
 

Abstract

Smirnov A.V., Gurianova Т. У. Article "New technologies in money management dynamic ". The well-known R. Vince's method of optimal fraction is analyzed. The method shortcomings are indicated. Three new algorithms of money managements are proposed. These money fraction estimations depends on P & L, (current investment risk level) characteristics on stationarity interval.

Введение

В мире постоянно растет интерес инвесторов к практической реализации моделей и алгоритмов динамического управления капиталом (ДУК). Задача любого инвестора - в максимально короткий срок умножить свой первоначальный капитал и, одновременно, противостоять пагубному влиянию присутствующих
инвестиционных рисков. В своей монографии Р. Вине разработал оригинальную теорию «оптимального f» - оптимальной части капитала при реинвестировании [1]. Проведенные нами в [2] исследования Показали, что теоретические изыскания Р. Винса нуждаются в серьезной корректировке. Применение их на практике может привести трейдеров и портфельных менеджеров к существенному ущербу. Данная работа является органическим продолжением [2]. Она направлена на изыскание новой модели и новых алгоритмов ДУК на основе современных достижений в области теории вероятностей, математической статистики и теории управления.

Постановка задачи

Главной задачей настоящей работы является разработка новой адекватной модели и эффективных алгоритмов ДУК. Новая модель и алгоритмы ДУК должны учитывать нестационарный стохастический характер функционирования управляемой экономической системы. Особое место при этом имеет доброжелательная критика модели Р. Винса и ее сравнение с предложенной.

Критика исходной модели Р. Винса

Сущность предложенной в [1] Р. Винсом модели ДУК заключается в следующем: автор считает, что достаточно короткая реализация случайных выигрышей и проигрышей (Р&L) экономической системы, состоящей из n элементов, способна адекватно ее характеризовать на достаточно продолжительном интервале времени (бесконечные игры). Свою модель он  строит на неоднократном повторении этой короткой реализации Р&L₁, Р&L₂,… Р&L_n, Р&L₁, Р&L₂,… Р&L_n, и т.д. При этом он справедливо считает, что «оптимальное f»,  определяемое им по n элементам скользящего окна анализа, будет неизменной. Множитель первоначального капитала инвестора (TWR) при этом будет расти в степени N, где N - число повторов исходной реализации. С точки зрения теории вероятностей, при любом законе распределения значений случайных величин Р&L_i в  исходной реализации, закон распределения всей совокупности случайных величин Р&L_i при многократном повторении этой короткой реализации совершенно не зависит от исходного закона. Плотность вероятностей этой реализации представляет собой сумму из n δ-функций с одинаковыми коэффициентами, равными 1/n. Таким образом, предложенная в [1] Р. Винсом  модель ДУК - это модель детерминированной экономической системы, которая совершенно не учитывает нестационарный характер развития экономики и управляемой системы. По нашему мнению, модель ДУК Р. Винса слишком академична, не адекватна реалиям и не может быть достаточно эффективной при ее реализации на практике.

 

Предлагаемая модель ДУК

Любая экономическая система при нестационарном характере внешних воздействий может быть описана одномерным законом распределения вероятностей ее выходных случайных величин Р&L_i, на интервале стационарности их реализации  τ_cm. В большинстве практических случаев это нормальный закон, который вытекает из центральной предельной теоремы теории вероятностей (когда на систему действует одновременно большое количество разнонаправленных случайных факторов). В этом случае на интервале стационарности τ_cm система характеризуется двумя числовыми характеристиками: математическим ожиданием  AHPR_n  и дисперсией  SD²_n, которые являются постоянными и не зависят от времени.

где AHPR_n , SD²_n  - соответственно математическое ожидание и дисперсия HPR,;n<=τ - время анализа.Нестационарную реализацию Р&L_i можно характеризовать с помощью соответствующих автокорреляционных функций R₁ (τ, t) _и R₂ (τ, t). Первая из них характеризует временные изменения AHPRn, а вторая - SD². От R₁ (τ, t) и R₂ (τ, t) можно легко перейти к максимальным интервалам автокорреляций, путем известных преобразований

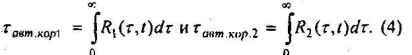
Интервал стационарности τ_ст меньше самой малой величины из τ_{авт.кор.1} и τ_{авт.кор.2}, которые проанализированы за N>>τ_cт достаточно продолжительный интервал времени. В случае использования этой модели, оценки f* - части капитала при реинвестировании даже при AHPR_n = const и SDl = const, будут отличаться друг от друга. Для их нахождения можно воспользоваться эмпирической формулой Р. Винса[1]

 

 

где Р& Lj - величина выигрыша или проигрыша системы, взятая с противоположным знаком; P&L_k - самый большой проигрыш системы (всегда со знаком «-»), вычисленный на интервале п<τ_ст. При    использовании    предложенной модели ДУК не корректно применять точечные оценки. Здесь целесообразно применение интервальных оценок f*.

 

Литература

 

1. Винc Р. Математика управления капиталом. Методы анализа риска для трейдеров ипортфельных менеджеров: Пер. с англ. - М.:Альпина Паблишер, 2001. -400 с.

2. Смирнов А.В., Гурьянова Т.В. Об «оптимальном /» Ральфа Винса. Наукові праці Донецького нашонального технічного университету, серія «Інформатика, кібернетика та обчислювальна техніка», вып. 9 (132), Донецк, ДонНТУ, 2008.-С. 216-220.

3. Левин Д.М., Кребиль Т.С. и др.Статистика для менеджеров с использованием MS Exel. 4-е изд.: Пер. с англ. - М.: «Вильяме», 2004.-1312 с.

4. Четыркин Е.М. Статистические методы прогнозирования. Изд. 2-е, перераб. и доп. - М.:Статистика, 1977.-200 с.

5. Мертенс А.В. Инвестиции: Курс лекций по современной финансовой теории. - К.: Киевское инвестиционное агентств, 1997. - XVI, 416 с.