Leo J. Zamansky, Ph.D., and David C. Stendahl. Стратегия безопасного процента управления активами

БЕЗОПАСНЫЙ ПРОЦЕНТ УПРАВЛЕНИЯ АКТИВАМИ

В данной статье рассматривается способ нахождения нового значения процента капитала для инвестирования в каждую сделку с целью максимизации дохода на капитал для достижения величины ограничивающих факторов, используя разновидность стратегии оптимального f.

В течение последних 4-х лет мы разработали и применили программные средства для оценки торговых систем, которые используют методы управления капиталом, а также изучили этих методов на торговые системы. Новая стратегия управления капиталом, названная «безопасным f» является одним из результатов этой работы. И здесь мы покажем, как найти размер безопасного процента капитала для инвестирования в каждую сделку для достижения величины ограничивающих факторов.

Безопасное f может быть как консервативной стратегией, так и к агрессивной, в зависимости от уровня допустимых максимальных расходов, выбранных данным трейдером. Это модификация стратегии оптимального f, представленной Ральфом Винсом в его «Перечне формул управления». Безопасное f отличается от оптимального f, т.к. оно учитывает значения прошлых издержек при расчете и использует информацию о ценах на базовые ценные бумаги.

Оптимальное f - это стратегия управления капиталом, которую можно использовать для улучшения и максимизации характеристик системы путем нахождения лучшего процента капитала для инвестирования в каждую сделку. Эта стратегия определяет, какой процент собственного капитала, инвестированного в сделку, принесет наибольший доход, основываясь на последовательности прошлых сделок. Т.к. трейдеры могут применять разнообразные стратегии управления капиталом, может быть полезным знать, каким бы был оптимальный размер инвестиций в каждом случае.

Концепция процентной или долевой стратегии сама по себе берет истоки из формулы Келли, которая оценивает процентное соотношение вашего капитала, участвующего в сделке, когда размеры потерь и выигрышей не равны.

b = соотношение размеров выигрышей при выишрышных сделках к рамзмеру проигрышей при проигрышных.

Простой пример: если бы у вас было три ставки - две выигрышных и одна проигрышная (1, 1, 0) – и вы получили и потеряли равную сумму:

Эта формула для вычисления f. Это формула применима, когда есть только два исход. Для трейдеров существует много исходов. Винс вводит оптимальное f, а для его нахождения нам надо максимизировать то, что Винс называет относительным конечным благосостоянием (Terminal Wealth Relative (TWR)). Задачу можно сформулировать таким образом:

HPRi(f)=1+(f((-доход от i-той сделки)/(Затраты от худшей проигрышной сделки))

Рисунок 1. Иллюстрирует задачу оптимизации, решаемую с помощью нахождения оптимального. Как модно видеть из Рис. 1, оптимальное f максимизирует конечную стоимость путем инвестирования правильной суммы в каждую сделку. Эта сумма равна f% от существующего капитала на момент начала сделки. Для нахождения значения оптимального f применяются расчеты на основе истории сделок.

Рис. 1 – Оптимальное f. Целью является использование оптимального f для управления торговым капиталом с целью максимизации относительного конечного благосостояния

История сделок должна быть с положительным балансом, в противном случае ни оптимальное f, ни любая другая стратегия не превратит проигрышную стратегию в выигрышную. Чем дольше применяется оптимальное f, тем больший конечный капитал будет получен в результате его применения.

В качестве примера представьте следующую игру. Эта игра может быть рассмотрена как упрощенная версия биржевой торговли. Вы совершаете 3 серии бросков монеты по 11 бросков каждая. Вы платите или вам платят только по окончании каждой серии. Для того, чтобы принять участие в игре, вам нужно заключить одну или более сделок. Цена одной сделки, предположим, $ 10 000. Бросок монеты эквивалентен точке открытия сделки. Выигрыш (или проигрыш) за один бросок составляет, предположим, $ 500.

Если вы заплатили $10 000 за одну сделку и выиграли восемь раз, а проиграли 3, то вы получили $2 500. Или если вы заплатили $20 000 за две сделки и выиграли семь раз, а проиграли 4, то вы получили $3000. В игре, в которую вы играете, за каждую оплаченную сделку вы выиграли 6 раз из 11 в первой и второй серии бросков и проиграли 5 раз в третьей. Это дает вам результат 1, 1, 0 – вы дважды выиграли и один раз проиграли.

Ниже приведены результаты каждой серии вашей игры

Теперь, предположим, у вас есть $100 000. Найдем оптимальное f на основе исхода 1, 1, 0. Получим сделки по $500,

Эта функция достигает максимума при f=1/3. Это значит, что оптимальное f указывает на необходимость инвестировать в каждую сделку третью часть ваших денег, что для первой сделки составит $33 333. Рассчитайте свои максимальные потери за игру, используя оптимальное f. Эти $ 33 333 позволят вам заключить три сделки, как и в первой серии. Предположим, вы выиграли $500 процентов за сделку, что в сумме дало $1500. Ваш суммарный капитал после первой серии составляет $33 833, что снова позволяет вам заключить три сделки.

Поскольку вы теряете $500 за каждый 0 в серии, то в течение второй серии вы потеряете $2500 после первых пяти бросков. Это значит, что к настоящему моменту ваш проигрыш составит $7500 за серию, или $6000 суммарных потерь капитала. Что составит 7500 деленное на 101500=0,0739 или 7,39% капитала к началу 2-й серии. Это максимальная торговая потеря.

Как видно из наших расчетов, у оптимального f существует несколько недостатков. Прежде всего, эта стратегия приводит к стремительному возрастанию количества оплачиваемых сделок. Как правило, это приводит к неприемлемо большим расходам.

Второе ограничение для применения оптимального f состоит в том, что эта стратегия психологически нежелательна для среднего трейдера, имеющего дело с риском. Также может иметь место нереалистичное допущение, зависящее от участника торгов, о существовании ликвидности или о том, что торговая система будет все еще действующей, приводящее к геометрическому приращению числа поданных сделок.

И, наконец, оптимальное f не принимает во внимание последовательность, в которой находится сделка: оно не учитывает сокращение капитала.

Эти проблемы приводят к очень ограниченному применению стратегии оптимального f в торговом сообществе. Ключевой вопрос в том, сколько вам следует инвестировать в игру, если у вас стоят ограничения по максимальным потерям? Это может быть и абсолютное значение (в долларах), и относительное значение (в процентном соотношении). Если ваши ограничения выше, чем $7 500 (предположим, $10 000), то ничего не изменится и оптимальное f будет решением. Однако если ваши ограничения по максимально допустимым потерям в течение игры будут, предположим, $50 000, тогда вы сможете провести только две сделки из трех. То же верно, если мы предположим, что ограничения на максимально допустимые потери составляют 5%. Это значит, что для вас предпочтительней в этой игре инвестировать оптимальный объем капитала в размере 20% . Это та доля, которую мы называем безопасным f. Каждый трейдер использует свое значение безопасного f, поскольку у каждого трейдера своя восприимчивость к потерям.

Для того, чтобы сформулировать проблему, разрешаемую с помощью безопасного f, мы добавили ограничение при вычислении оптимального f . Ограничение может отражать максимально допустимые потери ( и/или другие характеристики. Это более консервативная стратегия, преимущество которой состоит в нахождении доли капитала, инвестируемого в каждую сделку, которая принесет наибольший возможный доход при максимально допустимых издержках. Давайте переформулируем проблему нахождения оптимального f путем добавления ограничений на потери.

Допуская , что максимальные издержки (f) меньше или равны максимальным допустимым издержкам трейдера, решение, которое максимизирует TWR, будет безопасным f. Постановка задачи, учитывающей потери, приведена на рисунке 2.

Эта постановка задачи такова, что решение максимизирует TWR и гарантирует, что издержки при построении системы по прошлым данным не превысят размера, установленного трейдером – значение D. Это значение относится к максимально допустимым потерям. (Это могут быть потери как от сделки, так и потери капитала, или другая оценка риска, или нескольких рисков одновременно. Это могут быть ограничения по мере волатильности. Другие ограничения могут быть учтены таким же образом, как показано на рис. 1, путем простого добавления большего числа ограничений.) Рис.2 показывает цены в качестве дополнительных данных, необходимых для расчетов.

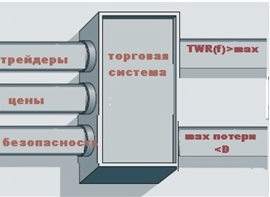
Рис. 2 – Безопасное (f). Постановка задачи, учитывающая максимальные потери в наборе ограничений при максимизации относительного конечного благосостояния.

Если максимальные допустимые издержки меньше, чем максимальные издержки за рассматриваемый период, то значение безопасного f будет равно значению оптимального f, и стратегия безопасного f принесет те же результаты, что и стратегия оптимального f. Рис. 3 показывает график TWR и максимальные потери по отношению к значению f. Рис. 4 представляет собой сравнение оптимального и безопасного f.

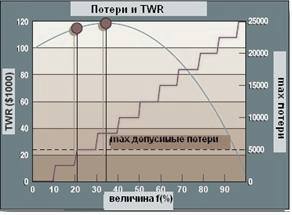
Рис. 3 – Сравнение соотношения. Здесь изображено относительное конечное благосостояние и максимальные потери, соотнесенные с величиной f. C ростом f увеличиваются и максимальные потери. Оптимальное f достигает максимума при 33,3%. Когда максимальные потери устанавливаются на уровне $5000, величина безопасного f составляет 20% капитала.

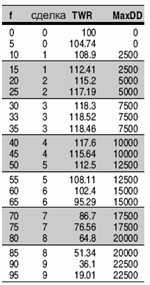
Рис. 4 – Возрастающее значение f для процентного соотношения изменения величины капитала после каждой сделки. Относительное конечное благосостояние достигает максимума при 118,52.

Пусть f^s будет значением безопасного f, D – максимально допустимые издержки, TWR (f,D) - относительное конечное благосостояние для данных значений f и D, delta –желаемая точность для вычисления безопасного f.

Если максимально допустимые издержки больше или равны максимальным историческим издержкам, тогда конец. В противном случае – шаг 3.

- Рассчитать MDD(f) – максимальные издержки для доли капитала f, которая будет инвестирована в каждую сделку, используя информацию о сделках и ценах. Если MDD(f)<D, тогда рассчитать TWR(f,D) и сохранить значение f и TWR(f,D).

- найти значение f такое, чтобы оно отвечало максимуму всех сохраненных TWR(f,D). Это значение является безопасным f, т.е. f^s.

Такая же логика может быть применена для нахождения безопасного f для ограничений, отличных от максимальных издержек.

Для сравнения рассмотрим простую систему выхода для продажи немецких марок. Система покупает при повышении цены выше уровня поддержки на 20-й день и продает при падении цены ниже уровня поддержки на 10-й день. Код TradeStation для этих пробоев системы приведен ниже.

Как стратегия оптимального f, так и стратегия безопасного f, повышают чистую прибыль за счет снижения максимальных издержек. Возрастание максимальных издержек по отношению к чистой прибыли ясно показывает существенное различие между этими двумя стратегиями. Хотя стратегия оптимального f приводит к намного большей чистой прибыли, соотношение чистая прибыль/максимальные издержки для стратеги безопасного f в семь раз выше, чем то же значение для оптимального f. Рисунок 5 показывает различия между стратегиями.

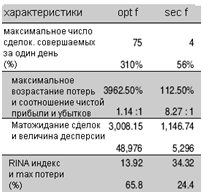
Рис. 5 – Простая система выхода, покупающая марки и выходящая из торгов при пробое на 20-й и 10-й дни торгов соответственно. При использовании оптимального f максимальное число сделок достигает 75 за один день и максимальные потери составляют 65,8%. При использовании безопасного f число сделок равно 4, а максимальные потери – 24,4%.

На протяжение 12 лет испытаний (1985-97) стратегия оптимального f попыталась бы продать 75 сделок по немецким маркам в один день. Стратегия безопасного f, с другой стороны, продавала бы максимум 4 сделки по немецким маркам за один раз.

Характеристики системы выхода использованием оптимального и безопасного f показаны на рис. 6 и 7.

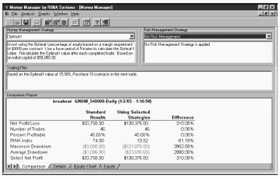
Рис. 6 – Статистические характеристики. Здесь показаны статистические характеристики простой системы выхода при продаже марок с использованием стратегии оптимального f. В первой колонке представлены результаты типовых испытаний при совершении одной сделки. Во второй колонке стратегия оптимального f применяется к последним пяти сделкам. Третья колонка показывает разницу между двумя стратегиями.

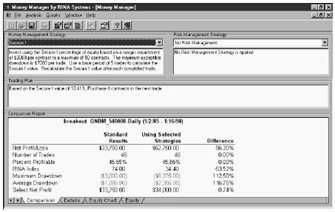
Рис. 7 – Статистические характеристики. Здесь показаны статистические характеристики простой системы выхода при продаже марок с использованием стратегии безопасного f. Описание колонок такое же, как на рис. 6

Рис. 8 и 9 иллюстрируют соответствие кривых Underwater Equity для обеих стратегий. Рисунок 9 показывает процент потерь, начиная с конца каждого месяца, относительно предыдущего пика и отражает максимально возможную коррекцию в процентах на каждом шаге. Эти рисунки показывают большую разницу в потерях капитала между оптимальным и безопасным f.

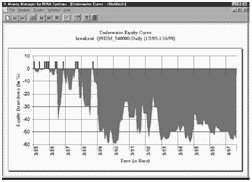
Рис. 8 – Кривая Underwater Equity. C использованием оптимального f эта диаграмма показывает процент потерь начиная с конца каждого месяца, рассчитанных на основе максимумов за предыдущий месяц и отражающих максимально возможную коррекцию в процентах на каждом шаге.

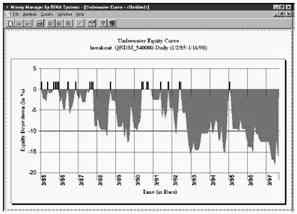
Рис. 9 – Кривая Underwater Equity. C использованием безопасного f эта диаграмма показывает процент потерь начиная с конца каждого месяца, рассчитанных на основе максимумов за предыдущий месяц и отражающих максимально возможную коррекцию в процентах на каждом шаге.

И наконец, рис. 10 и 11 описывают кривые доходности для оптимального и безопасного f соответственно.

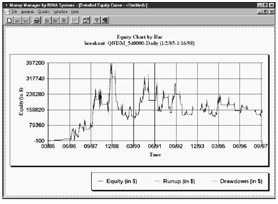
Рис. 10 – Кривая доходности. Здесь показана кривая доходности с использованием оптимального f. Она нестабильно возрастает с пиком в 1998.

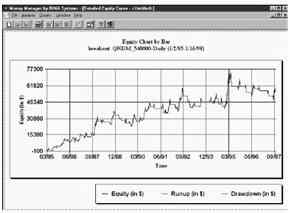
Рис.11 – Кривая доходности. Здесь показана кривая доходности при использовании безопасного f. Обратите внимание на ее устойчивый рост.

Стратегия безопасного f для управления капиталом дает трейдеру возможность максимизировать доход на том уровне риска, который он решает принять. Стратегия безопасного f может быть как консервативной, так и агрессивной стратегией, в зависимости от уровня максималыьно допустимых издержек, выбранного рейдером. Этот уровень может быть установлен каждым трейдером индивидуально в соответствии с его предпочтениями. Стратегия безопасного f может быть применена как для механических, так и немеханических торгов, а также для повышения прибыльности на любом рынке.

2. Zamansky, Leo J., and David Stendahl [1997]. “Dynamic zones,” Technical Analysis of STOCKS & COMMODITIES, Volume 15: July.

3. Zamansky, Leo J., and David Stendahl [1997]. “Evaluating system efficiency,” TechnicalAnalysis of STOCKS & COMMODITIES, Volume 15: October.

Стратегия безопасного процента управления активами

Leo J. Zamansky, Ph.D., and David C. Stendahl

Перевод с английского: Кравченко П.П.