Theme of master's work:
The Factors Ranging of the Internet Shop Advancement by Multisets
Summary of research and developments
Will consider the new approach of ranging of factors of advancement the Internet of shop which exist in a considerable quantity and with differing values of signs. As the problem decision application of the device of multisets which allows to consider all factors and their signs is offered.
Concepts of multisets
Multiattribute objects Ai, i=1, …, n it is usually accepted to represent as vectors or trains qi = (![]() …,
…,![]() ) in space Q=Q1 ?… ?Qm, where Qs = {
) in space Q=Q1 ?… ?Qm, where Qs = {![]() } – a continuous or discrete scale of s th sign, es=1?hs, s=1, …, m. The situation essentially becomes complicated, if one can correspond to same object Ai not, and some m-dimensional vectors. For example, object Ai is estimated k by independent experts on m to criteria, or it is necessary to consider simultaneously m the parametres of object Ai measured k in the various ways. In such cases object Ai is represented in m-dimensional space Q any more one vector qi, and the group consisting from k of vectors {qi (1), …, qi (k)} a kind qi (j) = (
} – a continuous or discrete scale of s th sign, es=1?hs, s=1, …, m. The situation essentially becomes complicated, if one can correspond to same object Ai not, and some m-dimensional vectors. For example, object Ai is estimated k by independent experts on m to criteria, or it is necessary to consider simultaneously m the parametres of object Ai measured k in the various ways. In such cases object Ai is represented in m-dimensional space Q any more one vector qi, and the group consisting from k of vectors {qi (1), …, qi (k)} a kind qi (j) = (![]() …,
…,![]() ), j=1, …, k which should be considered as a unit. Thus, obviously, values of signs can be similar, differing and even inconsistent, that in turn can lead несравнимости m-dimensional vectors qi (j), characterising the same object Ai.
), j=1, …, k which should be considered as a unit. Thus, obviously, values of signs can be similar, differing and even inconsistent, that in turn can lead несравнимости m-dimensional vectors qi (j), characterising the same object Ai.
Set of such "compound" objects can have in space Q difficult structure, difficult enough for the analysis. Uneasy to enter in this space and the metrics for measurement of distances between objects. The specified difficulties can be overcome if to take advantage of a representation different way multiattribute the objects, based on a formalism of the theory of multisets [1].
Let's enter instead of direct product m scales of signs Q=Q1 ?… ?Qm the generalised scale of signs – set G={Q1, …, Qm}, consisting of m groups of signs, and we will present object Ai in such symbolical kind:
Ai = {kAi (q11) •q11, …, kAi (![]() ) •
) •![]() , …, kAi (qm1) •qm1, …, kAi (
, …, kAi (qm1) •qm1, …, kAi (![]() ) •
) •![]() },
},
Where the number kAi (![]() ) specifies, how many time sign
) specifies, how many time sign ![]() IQs meets in the description of object Ai, the sign • designates frequency rate of a sign
IQs meets in the description of object Ai, the sign • designates frequency rate of a sign![]() . Set G characterises properties of set of objects A = {A1..., An}. Such record of object Ai represents it as set with repeating elements or multiset.
. Set G characterises properties of set of objects A = {A1..., An}. Such record of object Ai represents it as set with repeating elements or multiset.
Over multisets are carried out traditional teoretiko-mno-zhestvennye operations, such as association, crossing, subtraction, addition, a symmetric difference, direct product, and a number of new operations: addition, multiplication, multiplication to number, and also linear combinations of operations. New types of operations over multisets open new possibilities for grouping multiattribute objects. For example, group Xt of objects can be received as sum Xt=aiAi, association Xt=UiAi or crossing Xt=IiAi of multisets Ai describing objects Ai, or as a linear combination of various multisets of kind Xt=aiti•Ai, Xt=Uiti•Ai or Xt=Iiti•Ai, ti> 0.
Various classes of metric spaces of multisets (A, d) are defined by following metrics (pseudo-metrics) [1]:
d1p (A, B) = [m (A?B)] 1/p; d2p (A, B) = [m (A?B) /m (Z)] 1/p;
d3p (A, B) = [m (A?B) /m (AUB)] 1/p,
Where p - an integer, m - the multiset measure, the valid non-negative function set on algebra of multisets L (Z).
Representation multiattribute objects by means of multisets allows to expand considerably a circle of considered problems and to solve various problems of classification, sorting, ranging, cluster the analysis of objects.
The Mathematical Model of Factors Ordering of Internet Shop Advancement
In considered model we range the factors of Internet shop advancement. As there is considerable quantity of promotion factors cannot be established between them certain linear or nonlinear dependence, then we will apply the multisets means to ranging of factors.
On the basis of the collected statistical data, which are a resulted in table 1, we will allocate as objects of the analysis the set which ![]() , which represents the basic indicators of an overall performance of Internet shop:
, which represents the basic indicators of an overall performance of Internet shop:
- A1 - Quantity of viewings:
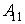 - High quantity of viewings;
- High quantity of viewings;
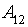 - Average quantity of viewings;
- Average quantity of viewings;
 - Low number of viewings;
- Low number of viewings;
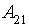 - High level of orders;
- High level of orders;
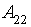 - An average level of orders;
- An average level of orders;
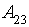 - Low level of orders;
- Low level of orders;
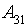 - Considerable quantity of visitors;
- Considerable quantity of visitors;
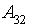 - Average quantity of visitors;
- Average quantity of visitors;
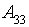 - Small quantity of visitors;
- Small quantity of visitors;
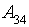 - Very small quantity of visitors.
- Very small quantity of visitors.
For an estimation of an overall performance of Internet shop we choose the factors influencing set of the analysis of objects:
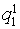 - "Yes" delivery has been made;
- "Yes" delivery has been made;
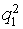 - "Is not present" there was no delivery.
- "Is not present" there was no delivery.
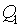 -Mass delivery:
-Mass delivery:
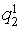 - Above an average (> 150);
- Above an average (> 150);
 - Average (<150).
- Average (<150).
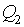 - Quantity of external references to a resource:
- Quantity of external references to a resource:
 - "Yes" it has been made
- "Yes" it has been made
 - "Is not present" it has not been made
- "Is not present" it has not been made
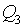 - Placing in catalogues
- Placing in catalogues
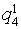 - It is made (> 10)
- It is made (> 10)
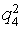 - An average (> 5, <10)
- An average (> 5, <10)
 - It is not enough (<5)
- It is not enough (<5)
 - Placing of banners
- Placing of banners
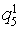 - To the full (> 5)
- To the full (> 5)
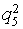 - An average (<5)
- An average (<5)
 - Site registration in searchers
- Site registration in searchers
Except an estimation of each factor of set And we will carry each object of the analysis to one of sets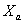 (
(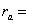 factor significant for Internet shop advancement) or (
factor significant for Internet shop advancement) or (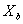
 factor insignificant for Internet shop advancement).
factor insignificant for Internet shop advancement).
Transformed for processing by means of the multisets means sample are resulted in table 2.Table 2. Sample for processing by means of multisets means
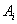
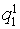
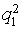
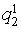
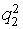



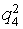

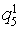
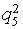
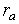
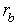
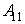
0
1
0
1
0
1
0
0
1
1
0
1
0

3
3
0
6
2
3
0
3
3
5
1
1
0
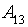
0
1
0
1
1
0
0
1
0
1
0
0
1

0
0
0
0
0
0
0
0
0
0
0
1
0
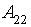
2
5
0
7
4
3
0
4
3
6
1
1
0
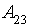
1
0
0
1
0
1
0
0
1
1
0
0
1

0
1
0
1
0
1
0
0
1
1
0
1
0
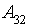
2
3
0
5
3
2
0
3
2
4
1
1
0

1
1
0
2
1
1
0
1
1
2
0
0
1
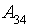
0
0
0
0
0
0
0
0
0
0
0
0
1
Let's unite objects Aij concerning set classes Xa and Xb. We will receive the transformed table of the decisions which lines correspond to multisets Xa and Xb (table 3). We consider, that object Aij belongs to the class Ха if,
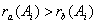 differently the object belongs to the class Хb
differently the object belongs to the class Хb Table 3. Results of division of criteria on significant Хa and insignificant Xb
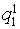

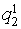

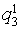
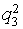
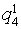
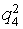
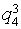
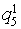
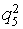
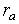
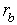
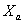
7
13
0
20
9
10
0
10
10
17
3
6
0
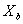
1
2
0
4
2
2
0
2
2
4
0
0
4
Let's calculate distance d1 for each factor according to the formula:
d1 (Qsa *, Qsb *) = axIQs * | kXa (xj) -kXb (xj) |, d1 (Ra, Rb) = axIR|kXa (xj) -kXb (xj) |.
Results of calculation are resulted in table 4.Table 4. Results of calculation of distances d1
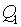

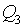
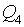
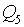
d1
17
16
15
16
16
Let's estimate accuracy of approximation on s th group of signs:
rs = d (Qsa *, Qsb *) /d (Ra, Rb).
Results of an estimation of accuracy of approximation are given in table 5.
Table 5. Results of an estimation of accuracy of approximation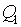
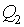
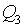


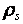
1,7
1,6
1,5
1,6
1,6
Let's choose approximating signs qs* for each factor (the approximating considers that sign for which the condition for table 2 data is satisfied
The ranging of approximating signs on distance size d1 shows, that the most important factor of advancement of Internet shop is the factor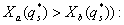
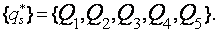
Let's order approximating signs qs* on decrease of accuracy of approximation rs:
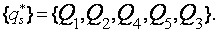
Having chosen some desirable value of accuracy of approximation r0, we will receive the generalised solving rules for selection.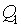 , which characterising the organisation the mass delivery.
, which characterising the organisation the mass delivery.
The literature
1. Петровский А.Б. Упорядочение и классификация объектов с противоречивыми признаками // Новости искусственного интеллекта. - 2003. - №4. - 17 с.
2. Миркин Б.Г. Анализ качественных признаков и структур. - М.: Статистика, 1980.
3. Петровский А.Б. Пространства множеств и мультимножесв. - Москва: Едиториал УРСС, 2003. - 248 с.
4. Журавлев Ю.И. Корректные алгебры над множествами некорректных (эвристических) алгоритмов.I,II,III.//Кибернетика, 1977, №4, 14-21; 1977, №6, 21-27; 1978, №2, 35-43.
5. Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. Вербальный анализ решений. - М.: Наука, Физматлит, 1996.
6. Ларичев О.И., Прохоров А.С., Петровский А.Б., Стернин М.Ю., Шепелев Г.И. Опыт планирования фундаментальных исследований на конкурсной основе.//Вестник АН СССР, 1989, №7, 51-61.
7. Миркин Б.Г. Анализ качественных признаков и структур. - М.: Статистика, 1980.
8. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. - М.: Физматлит, 2002.
9. Арлазаров В.Л., Логинов А.С., Славин О.А. Характеристики программ оптического распознавания текста.//Программирование, 2002, №3, 45-63.
10. Дорофеюк А.А. Алгоритмы автоматической классификации.//Автоматика и телемеханика. 1971, №12, 78-113.



