Тема випускної роботи:
Ранжування факторів просування інтернет-магазину за допомогою апарата мультимножин
Реферат з теми випускної роботи
Розглянемо новий підхід ранжування факторів просування Інтернет магазину, які існують у великій кількості й зі значеннями, що відрізняються ознаками. Як рішення проблеми пропонується застосування апарата мультимножин, що дозволяє враховувати всі фактори і їхні ознаки.
Поняття мультимножин
Багатозначні об'єкти Ai, i=1,…,n звичайно прийнято представляти як вектори або кортежі qi=(![]() ,…,
,…,![]() ) у просторі Q=Q1?…?Qm, де Qs={
) у просторі Q=Q1?…?Qm, де Qs={![]() } – безперервна або дискретна шкала s-го ознаки, es=1?hs, s=1,…,m... Ситуація істотно ускладнюється, якщо тому самому об'єкту Ai може відповідати не один, а кілька m-мірних векторів. Наприклад, об'єкт Ai оцінюється k незалежними експертами по m критеріях, або необхідно одночасно врахувати m параметрів об'єкта Ai, обмірюваних k різними способами. У таких випадках об'єкт Ai представляється в m-мірному просторі Q уже не одним вектором qi, а групою, що складається з k векторів {qi(1),…,qi(k)} виду qi(j)=(
} – безперервна або дискретна шкала s-го ознаки, es=1?hs, s=1,…,m... Ситуація істотно ускладнюється, якщо тому самому об'єкту Ai може відповідати не один, а кілька m-мірних векторів. Наприклад, об'єкт Ai оцінюється k незалежними експертами по m критеріях, або необхідно одночасно врахувати m параметрів об'єкта Ai, обмірюваних k різними способами. У таких випадках об'єкт Ai представляється в m-мірному просторі Q уже не одним вектором qi, а групою, що складається з k векторів {qi(1),…,qi(k)} виду qi(j)=(![]() ,…,
,…,![]() ), j=1,…,k, яка повинна розглядатися як єдине ціле. При цьому, мабуть, значення ознак можуть бути схожими, що розрізняються й навіть суперечливими, що у свою чергу може приводити до незрівнянності m-мірних векторів qi(j), що характеризують той самий об'єкт Ai.
), j=1,…,k, яка повинна розглядатися як єдине ціле. При цьому, мабуть, значення ознак можуть бути схожими, що розрізняються й навіть суперечливими, що у свою чергу може приводити до незрівнянності m-мірних векторів qi(j), що характеризують той самий об'єкт Ai.
Сукупність таких «складових» об'єктів може мати в просторі Q складну структуру, досить важку для аналізу. Непросто ввести в цьому просторі й метрику для виміру відстаней між об'єктами. Зазначені труднощі можна перебороти, якщо скористатися іншим способом подання багатозначних об'єктів, заснованим на формалізмі теорії мультимножини [1].
Уведемо замість прямого добутку m шкал ознак Q=Q1?…?Qm узагальнену шкалу ознак – безліч G={Q1,…,Qm},складається з m груп ознак, і представимо об'єкт Ai у такому символічному виді:
Ai = {kAi(q11)• q11,…,kAi(![]() )•
)•![]() ,…,kAi(qm1)•qm1,…, kAi(
,…,kAi(qm1)•qm1,…, kAi(![]() )•
)•![]() },
},
де число kAi(![]() ) указує, скільки разів ознака
) указує, скільки разів ознака ![]() IQs зустрічається в описі об'єкта Ai, знак • позначає кратність ознаки
IQs зустрічається в описі об'єкта Ai, знак • позначає кратність ознаки ![]() . Безліч G характеризує властивості сукупності об'єктів A={A1,...,An}. Такий запис об'єкта Ai представляє його як безліч із повторюваними елементами або мультимножина.
. Безліч G характеризує властивості сукупності об'єктів A={A1,...,An}. Такий запис об'єкта Ai представляє його як безліч із повторюваними елементами або мультимножина.
Над мультимножинами виконуються традиційні теоретико-множені операції, такі як об'єднання, перетинання, вирахування, доповнення, симетрична різниця, прямий добуток, і ряд нових операцій: додавання, множення, множення на число, а також лінійні комбінації операцій. Нові типи операцій над мультимножинами відкривають нові можливості для групування багатозначних об'єктів. Наприклад, група Xt об'єктів може бути отримана як сума Xt=aiAi, об'єднання Xt=UiAi або перетинання Xt=IiAi мультимножини Ai, що описує об'єкти Ai, або як лінійна комбінація різних мультимножин виду Xt=aiti• Ai, Xt=Uiti• Ai або Xt=Iiti• Ai, ti>0.
Різні класи метричних просторів мультимножин (A,d) визначаються наступними метриками (псевдометриками) [1]:
d1p(A,B) = [m(A?B)]1/p; d2p(A,B) = [m(A?B)/m(Z)]1/p;
d3p(A,B) = [m(A?B)/m(AUB)]1/p,
де p – ціле число, m – міра мультимножини, дійсна ненегативна функція, задана на алгебрі мультимножин L(Z).
Подання багатозначних об'єктів за допомогою мультимножин дозволяє значно розширити коло розглянутих проблем і вирішувати різноманітні завдання класифікації, сортування, ранжирування, кластерного аналізу об'єктів.
Математична модель ранжування факторів просування інтернет-магазину за допомогою аппарта мультимножин
У моделі, яка розглядається, ранжуємо фактори просування Інтернет-магазину. У зв'язку з тим, що факторів розкручування сайту велика кількість і не можна встановити між ними певної лінійної або нелінійної залежності застосуємо апарат мультимножин до ранжування факторів як до завдання багатокритеріального типу.
На основі статистичних даних, які аналізуються, наведених у таблиці 1, виділимо у якості об'єкту аналізу: множину ![]() , що містить основні показники ефективності роботи Інтернет-магазину:
, що містить основні показники ефективності роботи Інтернет-магазину:
- А1 – кількість переглядів:
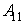 – висока кількість переглядів;
– висока кількість переглядів;
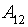 – середня кількість переглядів;
– середня кількість переглядів;
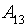 – низька кілкість переглядів;
– низька кілкість переглядів;
 – високий рівень замовлень;
– високий рівень замовлень;
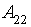 – середній рівень замовлень;
– середній рівень замовлень;
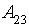 – низький рівень замовлень;
– низький рівень замовлень;
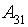 - велика кількість відвідувачів;
- велика кількість відвідувачів;
 - середня кількість відвідувачів;
- середня кількість відвідувачів;
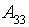 - маленька кількість відвідувачів;
- маленька кількість відвідувачів;
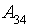 - дуже маленька кількість відвідувачів.
- дуже маленька кількість відвідувачів.
Для оцінки ефективності роботи Інтернет-магазина вибираємо критерії, що впливають на безліч аналізу об'єктів:
 - «так» було зроблене розсилання;
- «так» було зроблене розсилання;
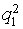 - «ні» не було розсилання.
- «ні» не було розсилання.
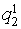 - вище за середнє (> 150);
- вище за середнє (> 150);
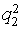 - середнє (<150).
- середнє (<150).
 - «так» було зроблено
- «так» було зроблено
 - «ні» не було зроблено
- «ні» не було зроблено
 - розміщено велика кількість банеров
- розміщено велика кількість банеров
 - розміщено середня кількість банеров
- розміщено середня кількість банеров
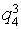 - розміщено низька кількість банеров
- розміщено низька кількість банеров
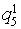 - повною мірою (> 5)
- повною мірою (> 5)
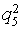 - середньо (<5)
- середньо (<5)
Перетворена для обробки за допомогою апарату мультимножин вибірка наведена в таблиці 2.
Таблиця 2. Вибірка для обробки за допомогою апарату мультимножин
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
3 |
3 |
0 |
6 |
2 |
3 |
0 |
3 |
3 |
5 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
2 |
5 |
0 |
7 |
4 |
3 |
0 |
4 |
3 |
6 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
2 |
3 |
0 |
5 |
3 |
2 |
0 |
3 |
2 |
4 |
1 |
1 |
0 |
|
1 |
1 |
0 |
2 |
1 |
1 |
0 |
1 |
1 |
2 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Об'єднаємо об'єкти Aij, що відповідають заданим класам Xa та Xb. Одержимо перетворену таблицю рішень, рядки якої відповідають мультимножинам Xa й Xb (таблиця 3). Зазначимо, що об'єкт Aij відносять до класу Ха, якщо ![]() , інакше об'єкт відносять до класу Хb
, інакше об'єкт відносять до класу Хb
Таблиця 3. Результати розподілу критеріїв на значимі Хa і незначимі Xb
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
13 |
0 |
20 |
9 |
10 |
0 |
10 |
10 |
17 |
3 |
6 |
0 |
|
1 |
2 |
0 |
4 |
2 |
2 |
0 |
2 |
2 |
4 |
0 |
0 |
4 |
Розрахуємо відстань d1 для кожного критерію відповідно до формули:
d1(Qsa*,Qsb*) = axIQs*|kXa(xj)-kXb(xj)|, d1(Ra,Rb) = axIR|kXa(xj)-kXb(xj)|.
Результати розрахунку наведені в таблиці 4.
Таблиця 4. Результати розрахунку відстаней d1
|
|
|
|
|
|
d1 |
17 |
16 |
15 |
16 |
16 |
Оцінимо точність апроксимації по s-ої групі ознак:
rs = d(Qsa*, Qsb*)/d(Ra, Rb).
Результати оцінки точності апроксимації дані в таблиці 5.
Таблиця 5. Результати оцінки точності апроксимації
|
|
|
|
|
|
|
1,7 |
1,6 |
1,5 |
1,6 |
1,6 |
Виберемо апроксимуючі ознаки qs* для кожного критерію (апроксимуючою будемо вважати ту ознаку, для якого виконується умова ![]() для даних таблиці 2):
для даних таблиці 2):
![]()
Упорядкуємо апроксимуючі ознаки qs* по убуванню точності апроксимації rs:
![]()
Вибравши деяке бажане значення точності апроксимації r0, одержимо узагальнені вирішальні правила для відбору критеріїв.
Ранжирування апроксимуючих ознак по величині відстані d1 показує, що найбільш важливим фактором просування Інтернет-магазину є критерій ![]() , що характеризує організацію масового розсилання.
, що характеризує організацію масового розсилання.
ЛІТЕРАТУРА
1. Петровский А.Б. Упорядкування й класифікація об'єктів із суперечливими ознаками // Новини штучного інтелекту. - 2003. - №4. - 17 с.
2. Миркин Б.Г. Аналіз якісних ознак і структур. - М.: Статистика, 1980.
3. Петровский А.Б. Простору безлічей і мультимножин. - Москва: Едиториал УРСС, 2003. - 248 с.
4. Журавльов Ю.И. Коректні алгебри над безлічами некоректних (евристичних) алгоритмів.I,II,III.//Кібернетика, 1977, №4, 14-21; 1977, №6, 21-27; 1978, №2, 35-43.
5. Ларичев О.И., Мошкович Е.М. Якісні методи прийняття рішень. Вербальний аналіз рішень. - М.: Наука, Физматлит, 1996.
6. Ларичев О.И., Прохоров А.С., Петровский А.Б., Стернин М.Ю., Шепелев Г.И. Досвід планування фундаментальних досліджень на конкурсній основі.//Вісник АН СРСР, 1989, №7, 51-61.
7. Миркин Б.Г. Аналіз якісних ознак і структур. - М.: Статистика, 1980.
8. Ногин В.Д. Прийняття рішень у багатокритеріальному середовищу: кількісний підхід. - М.: Физматлит, 2002.
9. Арлазаров В.Л., Логинов А.С., Славин О.А. Характеристики програм оптичного розпізнавання тексту.//Програмування, 2002, №3, 45-63.
10. Дорофеюк А.А. Алгоритми автоматичної класифікації.//Автоматика й телемеханіка. 1971, №12, 78-113.



