Тема выпускной работы:
Ранжирование факторов продвижения интернет-магазина с помощью аппарата мультимножеств
Реферат по теме выпускной работы
Введение
Рассматриваетя новый подход ранжирования факторов продвижения Интернет магазина, которые существуют в большом количестве и с отличающимися значениями признаков. В качестве решения проблемы предлагается применение аппарата мультимножеств, который позволяет учитывать все факторы и их признаки.
Понятия мультимножеств
Многопризнаковые объекты Ai, i=1,…,n обычно принято представлять как векторы или кортежи qi=(![]() ,…,
,…,![]() ) в пространстве Q=Q1?…?Qm, где Qs={
) в пространстве Q=Q1?…?Qm, где Qs={![]() } – непрерывная или дискретная шкала s-го признака, es=1?hs, s=1,…,m. Ситуация существенным образом усложняется, если одному и тому же объекту Ai может соответствовать не один, а несколько m-мерных векторов. Например, объект Ai оценивается k независимыми экспертами по m критериям, или необходимо одновременно учесть m параметров объекта Ai, измеренных k различными способами. В таких случаях объект Ai представляется в m-мерном пространстве Q уже не одним вектором qi, а группой, состоящей из k векторов {qi(1),…,qi(k)} вида qi(j)=(
} – непрерывная или дискретная шкала s-го признака, es=1?hs, s=1,…,m. Ситуация существенным образом усложняется, если одному и тому же объекту Ai может соответствовать не один, а несколько m-мерных векторов. Например, объект Ai оценивается k независимыми экспертами по m критериям, или необходимо одновременно учесть m параметров объекта Ai, измеренных k различными способами. В таких случаях объект Ai представляется в m-мерном пространстве Q уже не одним вектором qi, а группой, состоящей из k векторов {qi(1),…,qi(k)} вида qi(j)=(![]() ,…,
,…,![]() ), j=1,…,k, которая должна рассматриваться как единое целое. При этом, очевидно, значения признаков могут быть похожими, различающимися и даже противоречивыми, что в свою очередь может приводить к несравнимости m-мерных векторов qi(j), характеризующих один и тот же объект Ai.
), j=1,…,k, которая должна рассматриваться как единое целое. При этом, очевидно, значения признаков могут быть похожими, различающимися и даже противоречивыми, что в свою очередь может приводить к несравнимости m-мерных векторов qi(j), характеризующих один и тот же объект Ai.
Совокупность таких «составных» объектов может иметь в пространстве Q сложную структуру, достаточно трудную для анализа. Непросто ввести в этом пространстве и метрику для измерения расстояний между объектами. Указанные трудности можно преодолеть, если воспользоваться иным способом представления многопризнаковых объектов, основанным на формализме теории мультимножеств [1].
Введем вместо прямого произведения m шкал признаков Q=Q1?…?Qm обобщенную шкалу признаков – множество G={Q1,…,Qm}, состоящее из m групп признаков, и представим объект Ai в таком символическом виде:
Ai = {kAi(q11)•q11,…,kAi(![]() )•
)•![]() ,…,kAi(qm1)•qm1,…, kAi(
,…,kAi(qm1)•qm1,…, kAi(![]() )•
)•![]() },
},
где число kAi(![]() ) указывает, сколько раз признак
) указывает, сколько раз признак ![]() IQs встречается в описании объекта Ai, знак • обозначает кратность признака
IQs встречается в описании объекта Ai, знак • обозначает кратность признака ![]() . Множество G характеризует свойства совокупности объектов A={A1,...,An}. Такая запись объекта Ai представляет его как множество с повторяющимися элементами или мультимножество.
. Множество G характеризует свойства совокупности объектов A={A1,...,An}. Такая запись объекта Ai представляет его как множество с повторяющимися элементами или мультимножество.
Над мультимножествами выполняются традиционные теоретико-мно-жественные операции, такие как объединение, пересечение, вычитание, дополнение, симметрическая разность, прямое произведение, и ряд новых операций: сложение, умножение, умножение на число, а также линейные комбинации операций. Новые типы операций над мультимножествами открывают новые возможности для группирования многопризнаковых объектов. Например, группа Xt объектов может быть получена как сумма Xt=aiAi, объединение Xt=UiAi или пересечение Xt=IiAi мультимножеств Ai, описывающих объекты Ai, либо как линейная комбинация различных мультимножеств вида Xt=aiti•Ai, Xt=Uiti•Ai или Xt=Iiti•Ai, ti>0.
Различные классы метрических пространств мультимножеств (A,d) определяются следующими метриками (псевдометриками) [1]:
d1p(A,B) = [m(A?B)]1/p; d2p(A,B) = [m(A?B)/m(Z)]1/p;
d3p(A,B) = [m(A?B)/m(AUB)]1/p,
где p – целое число, m – мера мультимножества, действительная неотрицательная функция, заданная на алгебре мультимножеств L(Z).
Представление многопризнаковых объектов с помощью мультимножеств позволяет значительно расширить круг рассматриваемых проблем и решать разнообразные задачи классификации, сортировки, ранжирования, кластерного анализа объектов.
Математическая модель ранжирования факторов продвижения интернет-магазина с помощью аппарта мультимножеств
В рассматриваемой модели ранжируем факторы продвижение Интернет-магазина. В связи с тем, что факторов раскрутки сайта большое количество и нельзя установить между ними определенной линейной или нелинейной зависимости применим аппарат мультимножеств к ранжированию факторов как к задачи многокритериальньного типа.
На основе собранных статистических данных приведенных в таблице 1, выделим в качестве объектов анализа множество ![]() , которое представляет собой основные показатели эффективности работы Интернет-магазина:
, которое представляет собой основные показатели эффективности работы Интернет-магазина:
- А1 – количество просмотров:
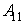 – высокое количество просмотров (>20000);
– высокое количество просмотров (>20000);
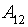 – среднее количество просмотров (больше 5000 и меньше 20000);
– среднее количество просмотров (больше 5000 и меньше 20000);
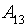 – низкое число просмотров (<5000);
– низкое число просмотров (<5000);
 – высокий уровень заказов (> 10 в неделю)
– высокий уровень заказов (> 10 в неделю)
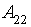 – средний уровень заказов (больше 2 в неделю и меньше 10 в неделю);
– средний уровень заказов (больше 2 в неделю и меньше 10 в неделю);
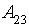 – низкий уровень заказов (< 2 в неделю);
– низкий уровень заказов (< 2 в неделю);
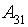 - большое количество посетителей (> 20000);
- большое количество посетителей (> 20000);
 - среднее количество посетителей (больше 5000 и меньше 20000);
- среднее количество посетителей (больше 5000 и меньше 20000);
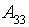 - маленькое количество посетителей (больше 1000 и меньше 5000);
- маленькое количество посетителей (больше 1000 и меньше 5000);
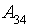 - очень маленькое количество посетителей (< 1000).
- очень маленькое количество посетителей (< 1000).
Таблица 1. Статистика сайта

Для оценки эффективности работы Интернет-магазина выбираем критерии, влияющие на множество анализируемых объектов:
 - «да» была сделана рассылка;
- «да» была сделана рассылка;
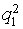 - «нет» не было рассылки.
- «нет» не было рассылки.
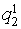 - выше среднего (> 150);
- выше среднего (> 150);
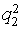 - среднее (<150).
- среднее (<150).
 - «да» было произведено;
- «да» было произведено;
 - «нет» не было сделано.
- «нет» не было сделано.
 - баннеров с ссылкой на сайт большое количество (>10);
- баннеров с ссылкой на сайт большое количество (>10);
 - баннеров с ссылкой на сайт среднее количество (больше 5 и меньше 10);
- баннеров с ссылкой на сайт среднее количество (больше 5 и меньше 10);
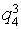 - баннеров с ссылкой на сайт маленькое количество (< 5).
- баннеров с ссылкой на сайт маленькое количество (< 5).
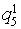 - в полной мере (> 5);
- в полной мере (> 5);
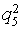 - недостаточно (<5).
- недостаточно (<5).
Преобразованная для обработки с помощью аппарата мультимножеств выборка приведена в таблице 2.
Таблица 2. Выборка для обработки с помощью аппарата мультимножеств
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
3 |
3 |
0 |
6 |
2 |
3 |
0 |
3 |
3 |
5 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
2 |
5 |
0 |
7 |
4 |
3 |
0 |
4 |
3 |
6 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
2 |
3 |
0 |
5 |
3 |
2 |
0 |
3 |
2 |
4 |
1 |
1 |
0 |
|
1 |
1 |
0 |
2 |
1 |
1 |
0 |
1 |
1 |
2 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Объединим объекты Aij, относящиеся к заданным классам Xa и Xb. Получим преобразованную таблицу решений, строки которой соответствуют мультимножествам Xa и Xb (таблица 3). Считаем, что объект Aij относится к классу Ха, если ![]() , иначе критерий относится к классу Хb
, иначе критерий относится к классу Хb
Таблица 3. Результаты разделения критериев на значимые Хa и незначимые Xb
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
13 |
0 |
20 |
9 |
10 |
0 |
10 |
10 |
17 |
3 |
6 |
0 |
|
1 |
2 |
0 |
4 |
2 |
2 |
0 |
2 |
2 |
4 |
0 |
0 |
4 |
Рассчитаем расстояние d1 для каждого критерия согласно формуле:
d1(Qsa*,Qsb*) = axIQs*|kXa(xj)-kXb(xj)|, d1(Ra,Rb) = axIR|kXa(xj)-kXb(xj)|.
Результаты расчета приведены в таблице 4.
Таблица 4. Результаты расчета расстояний d1
|
|
|
|
|
|
d1 |
17 |
16 |
15 |
16 |
16 |
Оценим точность аппроксимации по s-ой группе признаков:
rs = d(Qsa*, Qsb*)/d(Ra, Rb).
Результаты оценки точности аппроксимации даны в таблице 5.
Таблица 5. Результаты оценки точности аппроксимации
|
|
|
|
|
|
|
1,7 |
1,6 |
1,5 |
1,6 |
1,6 |
Выберем аппроксимирующие признаки qs* для каждого критерия (аппроксимирующим считаем тот признак, для которого выполняется условие ![]()
![]()
Упорядочим аппроксимирующие признаки qs* по убыванию точности аппроксимации rs:
![]()
Выбрав некоторое желаемое значение точности аппроксимации r0, получим обобщенные решающие правила для отбора критериев раскрутки интернет - магазина.
Ранжирование аппроксимирующих признаков по величине расстояния d1 показывает, что наиболее важным фактором продвижения Интернет-магазина является критерий ![]() , характеризующий организацию массой рассылки.
, характеризующий организацию массой рассылки.
ЛИТЕРАТУРА:
1. Петровский А.Б. Упорядочение и классификация объектов с противоречивыми признаками // Новости искусственного интеллекта. - 2003. - №4. - 17 с.
2. Миркин Б.Г. Анализ качественных признаков и структур. - М.: Статистика, 1980.
3. Петровский А.Б. Пространства множеств и мультимножесв. - Москва: Едиториал УРСС, 2003. - 248 с.
4. Журавлев Ю.И. Корректные алгебры над множествами некорректных (эвристических) алгоритмов.I,II,III.//Кибернетика, 1977, №4, 14-21; 1977, №6, 21-27; 1978, №2, 35-43.
5. Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. Вербальный анализ решений. - М.: Наука, Физматлит, 1996.
6. Ларичев О.И., Прохоров А.С., Петровский А.Б., Стернин М.Ю., Шепелев Г.И. Опыт планирования фундаментальных исследований на конкурсной основе.//Вестник АН СССР, 1989, №7, 51-61.
7. Миркин Б.Г. Анализ качественных признаков и структур. - М.: Статистика, 1980.
8. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. - М.: Физматлит, 2002.
9. Арлазаров В.Л., Логинов А.С., Славин О.А. Характеристики программ оптического распознавания текста.//Программирование, 2002, №3, 45-63.
10. Дорофеюк А.А. Алгоритмы автоматической классификации.//Автоматика и телемеханика. 1971, №12, 78-113.




