У статистичній моделі оперують показниками, обчисленими для якісно однорідних масових явищ (сукупностей). Вираження моделі у вигляді функціональних рівнянь використають для розрахунку середніх значень моделюємого показника по наборі заданих величин і для виявлення ступеня впливу на нього окремих факторів.
        Залежно від пізнавальної мети статистичні моделі підрозділяються на структурної, динамічні й моделі зв'язки. Нас цікавлять саме моделі зв'язку, і серед них найчастіше використовивався кореляційний і регресійний аналіз [4,5,6].

Кореляційний аналіз

        Кореляційним зв'язком є такий статистичний зв'язок, при якому різним значенням однієї змінної відповідають різні середні значення іншої. Основною особливістю кореляційного аналізу варто визнати те, що він установлює лише факт наявності зв'язку й ступінь її тісноти, не розкриваючи її причин.
        Задачі кореляційного аналізу зводяться до виміру тісноти зв'язку між ознаками, що варіюють, визначенню невідомих причинних зв'язків (причинний характер яких, повинен бути з'ясований за допомогою теоретичного аналізу) і оцінці факторів, що роблять найбільший вплив на результативну ознаку.
        Частіше використовується лінійний коефіцієнт кореляції. Значення r = -1 свідчить про наявність жорстко детермінованої обернено пропорційного зв'язку між факторами, r = +1 відповідає жорстко детермінованому зв'язку із прямо пропорційною залежністю факторів.
        Підсумовуючи, слід зазначити, що кореляційний аналіз вимагає для його застосування теоретичного аналізу даних для виявлення причинного характеру зв'язків. Також необхідна попередня підготовка даних для аналізу: угруповання, виключення аномальних спостережень, перевірка нормальності одномірного розподілу, усунення мультиколінеарності й уточнення набору показників шляхом розрахунку парних коефіцієнтів кореляції.

Регресійний аналіз

        Задачі регресійного аналізу - вибір типу моделі (форми зв'язку), установлення ступеня впливу незалежних змінних на залежну й визначення розрахункових значень залежної змінної (функції регресії).
        При рішенні задачі апроксимації за допомогою регресійного аналізу найбільш простим варіантом є лінійний однофакторний регресійний аналіз, коли передбачається лінійна залежність між фактором (входом) і параметром (виходом):

                                                        (1)

        Застосовуваний метод знаходження значень коефіцієнтів – МНК (метод найменших квадратів), тобто знаходить такі коефіцієнти, які мінімізують квадратичну помилку; або метод максимальної правдоподібності, що використовується для одержання оцінок параметрів генеральної сукупності за даними вибірки.
        Але на практиці часто доводиться визначати вид залежності не від одного фактору, а від декількох. Навмисна спрощення математичної моделі до лінійного виду робиться для зменшення об'єму розрахунків і спрощення виду функції залежності, допускаючи при цьому погрішність на лінеаризацію.
        Регресійний аналіз показує, по-перше, якість моделі, тобто ступінь того, наскільки дана сукупність іксів пояснює Y. Показник якості називається коефіцієнтом детермінації R2 і показує, який відсоток інформації Y можна пояснити поведінкою іксів. По-друге, регресійний аналіз обчислює значення коефіцієнтів В, тобто визначає, з якою силою кожний з Х впливає на Y. Множинний регресійний аналіз (багатофакторний) будує рівняння регресії у формі лінійного полінома із центрованим значенням змінних (факторів і параметра):

                               (2)

де - помилка апроксимації, так званий залишковий член, що фіксує ту частину інформації Y, що не пояснюється факторами Х..
        Недоліком класичного регресійного аналізу є спрощення форми математичної залежності до лінійної, що призводить до досить великої погрішності, тобто до втрати точності.
        Після одержання математичної моделі необхідно провести статистичний аналіз, що полягає у визначенні адекватності математичної моделі й оцінці значимості коефіцієнтів рівняння регресії.
        В ідеальній регресійній моделі незалежні змінні не корелюють один з одним. Однак сильна корелірованість змінних є досить частим явищем. Це приводить до збільшення помилок рівняння, зменшенню точність оцінювання, знижується ефективність використання регресійної моделі [7]. Тому вибір незалежних змінних, що включають у регресійну модель, повинен бути дуже ретельним.
         Пошук найкращої регресійної моделі являє собою досить громіздкий процес.
        Ще одним з недоліків класичного регресійного аналізу, в основі якого лежить МНК, є недостатня стійкість до змін вхідної інформації.
        Слід зазначити існування так називаного «парадокса регресії», що полягає в тім, що рівняння регресії Y від X значно відрізняється від залежності: X від Y.

Детерміновані моделі

        Детерміновані моделі [8] будуються на основі математично виражених закономірностей, що описують фізико-химічні процеси в об'єкті моделювання. Вони дозволяють однозначно знаходити значення змінних (які характеризують властивості об'єкта, що нас цікавлять) для будь-якої заданої сукупності значень вхідних змінних і конструктивних параметрів об'єктів моделювання.
        Для більшості процесів хімічної технології характерна наявність взаємодії потоків речовин, у яких відбуваються також хімічні перетворення. Тому в основу математичного опису, як правило, кладуть рівняння балансів мас й енергії в потоках, записані з урахуванням їхньої гідродинамічної структури.
        При використанні таких моделей особлива увага повинна приділятися розробці ефективних алгоритмів рішення системи рівнянь математичного опису.
        Часто детерміновані моделі надзвичайно складні й мають дуже складні граничні умови. Це приводить до необхідності використовувати в математичному описі, наприклад, конкретних потоків спрощені описи гідродинаміки на основі ідеалізованих моделей.
        При наявності в процесі декількох потоків речовин, а також потоків, що складаються з декількох фаз (наприклад, газ - рідина, рідина - тверде й т.п.), для кожного потоку й для кожної фази звичайно записуються свої рівняння гідродинаміки.
        При побудові детермінованої моделі важливе значення має розумна комбінація необхідної складності моделі із припустимими спрощеннями. Занадто складний математичний опис, що враховує множину, можливо, другорядних факторів й явищ, може виявитися неприйнятним через необхідність виконання величезного обсягу обчислень при рішенні вхідних у нього рівнянь. Навпаки, занадто спрощене математичний опис може привести до принципово неправильних висновків про властивості об'єкта моделювання.

Експертні моделі

        Побудова експертної моделі здійснюється за допомогою методів експертних оцінок [9] - це методи організації роботи з фахівцями-експертами й обробки думок експертів, виражених у кількісній й/або якісній формі з метою підготовки інформації для прийняття рішень.
        Рішення приймається за допомогою систематичного опитування фахівців, що володіють досвідом практичної роботи, здатних оцінити важливість питання, вибрати один з альтернативних шляхів його рішення. Ці методи застосовуються при відсутності необхідної інформації, обмеженості часу для рішення питання на основі формалізованих методів.
        Сутність експертних методів полягає в усередненні різними способами думок (суджень) фахівців-експертів по розглянутих питаннях. Від методу проведення опитування прямо залежить якість й об'єктивність експертної оцінки. Основним недоліком даного методу є те, що експертний метод повністю успадковує помилки експертів.
        Оскільки число експертів звичайно не перевищує 20-30, то формальна статистична погодженість думок експертів (установлена за допомогою тих або інших критеріїв перевірки статистичних гіпотез) може сполучатися з реально наявним поділом на групи, що робить подальші розрахунки не маючими змісту.

Огляд інструментальних засобів

Математична постановка задачі

        Якість отриманого коксу залежить значною мірою від підготовки вугілля і правильності складання вугільної шихти [2]. На коксохімічні заводи вугілля надходить звичайно з багатьох шахт і вуглезбагачувальних фабрик, і фахівець повинен не тільки знати властивості й склад вугілля, але й уміло складати з них суміш, що дає найкращий кокс. Складання вугільних шихт для коксування (шихтовання) виконується емпірично. Одне з основних вимог до якості коксу - висока міцність при достатньо великому розмірі.
        Основні характеристики, що описують шихту (вхідні параметри моделі):

• зольність (7-10%),
• серністість (0,5-3%),
• вологість (4-10%),
• марка вугілля.

        Основні характеристики, що описують кокс (вихідні параметри моделі):

• зольність (9-12%),
• серністість (1,6-2%),
• вологість (2-3%),
• структурна міцність(65-85%),
• вихід летучих речовин (1-2%),
• загальна пористість (45-55%),
• реакційна здатність (0,47-0,82 мл/(г*с)).

        Прийняті марки вугілля: Д - довгопламене, Г - газове, Ж - жирне, К - коксове, О - отощене, С - спікливе і Х - худе.
        Нехай множина представляє характеристики шихти. Потрібно знайти набір апроксимуючих функцій виду:

                                                        (3)

де – розрахункове значення залежної змінної, тобто одного з показників готового коксу;
     – фактори, показники шихти.
        При цьому задача зводиться до оптимізаційной задачі - мінімізації квадратичної помилки:

                                             (4)

де – помилка апроксимації;
     – апріорне значення вихідного параметра;
     – розрахункове значення вихідного параметра;
     – розмір вибірки.
                

Таблиця 1 - Обмеження на значення показників

Вибір та обгрунтування метода символьної регрессії

        Метод рішення задачі - метод символьної регресії (Рисунок 1 – Рішення задачі із використанням метода символьної регресії) генетичного програмування [15,16], що запропонований внаслідок своїх переваг у порівнянні з іншими методами моделювання. Даний метод є еволюційним методом, тобто він заснований на процесі природньої еволюції, що розвиває в процесі роботи алгоритму рішення, які являють собою математичні формули.

Рисунок 1 – Рішення задачі із використанням метода символьної регресії
(анімація: об'єм – 123 Кб; розмір – 183х697; кількість кадрів - 11; затримка між кадрами - 50 мс; затримка між останнім та першим кадрами - 200 мс; кількість циклів повторення - нескінчена)

        Генетичний алгоритм відрізняється від інших оптимізаційних і пошукових процедур наступними особливостями [17]:
             1. працює не з параметрами, а із закодованою множиною параметрів;
             2. здійснює пошук з популяції точок, а не з єдиної точки;
             3. використовує цільову функцію безпосередньо, а не її збільшення;
             4. використовує не детерміновані, а імовірнісні правила пошуку рішень;
             5. кожна нова популяція складається з життєздатних особин (хромосом);
             6. кожна нова популяція краще (у розумінні цільової функції) попередньої;
             7. у процесі еволюції наступна популяція залежить тільки від попередньої.
        Щоб еволюція була можлива, організми повинні відповідати 4 найважливішим властивостям:
             1. кожен індивід у популяції здатний до розмноження;
             2. відмінності індивідів друг від друга впливають на ймовірність їхнього виживання;
             3. кожен нащадок успадковує риси свого батька (подібне походить від подібного);
            4. ресурси для підтримки життєдіяльності й розмноження обмежені, що породжує конкуренцію й боротьбу за них.
         Всі ці властивості забезпечують оператори генетичного алгоритму.
        Завданням методу символьної регресії є знаходження такого математичного вираження функціональної залежності, що з мінімальною погрішністю апроксимує задані вибіркою значення.
        Для формування особини (математичного вираження) повинне бути визначене функціональна й термінальна множини [17,18]. Слід зазначити, що запропонований метод не вимагає використання заздалегідь визначеної форми функції залежності.
        Для даної задачі визначена функціональна множина: «+,-,*,/,^(зведення в ступінь)» і термінальна множина: значення факторів (Х) і речовинних констант із інтервалу [-5,5].
        Для представлення особини використана деревоподібна структура [17], приклад якої представлений на рисунку 2.

Рисунок 2 - Деревоподібне кодування особин

        Кожен вузол дерева являє собою або термінал (змінну, константу), або символ функції. Всі оператори функціональної безлічі вимагають двох аргументів. Якщо у вузлі записаний символ функції, то вузол повинен мати нащадків - аргументи функції, тобто термінали. Кінцеві вузли - це завжди термінали.
       Параметри алгоритму, що мають бути заданими: імовірність кросінговера, імовірність мутації, відсоток «еліти», кількість ітерацій алгоритму або точність рішення, розмір популяції.
        У якості фітнес-функції (функції оцінки придатності особини) у програмі буде використана:

                                           (5)

         Дана цільова функція є безперервною й стандартизованою.
        Значення придатності кожної особини (тобто її значення цільової функції) визначається як середньоквадратична помилка апроксимації даною особиною-формулою даних вибірки.
        На початку роботи алгоритму необхідно ініціалізувати популяцію особин. Загальним для всіх представлень є обмеження на розмір - на глибину дерева - не більше 20 рівнів. Найбільш ефективне значення цього параметра буде визначено експериментально.
        Для ініціалізації особин будуть застосовуватися два методи [17]. Перший - метод Росту дерев: дерево починає будуватися з кореня, запис у вузол виконується випадковим образом з множини, що включає термінальну й функціональну множини. Якщо вибирається функція, то процес рекурсивно триває для її нащадків. Другий метод - Повний. Будується дерево аналогічне методу росту, але вузли вибираються тільки з множини функцій, поки дерево не досягне заданої глибини. Потім заповнюються кінцеві вузли з множини змінних і констант.
        Використання тільки повного методу ініціалізації сприяє виродженню генетичного матеріалу й передчасної збіжності [17]. Тому застосовується комбінований метод. Популяція ділиться на 2 рівні частини, кожній частині ставиться своя максимальна глибина (наприклад, 20 й 10). Половина дерев з кожної групи будується за методом росту, інша - за повним методом.
        Критерієм завершення алгоритму є досягнення заданої точності рішення або виконання заданої кількості ітерацій еволюції.
        Для відбору особин-батьків буде використаний метод лінійного ранжирування [17], тому що він застосовний без модифікацій для задачі мінімізації й не вимагає масштабування для запобігання передчасної збіжності.
        Оператор кросінговера для деревоподібного представлення буде здійснюватися обміном піддерев. Випадковим чином вибираються 2 особини, а потім вузол в одному дереві й в іншому дереві. Для обміну піддеревами потрібно переконатися, що піддерева взаємозамінні, інакше - продовжувати підбір вузла. Піддерева відокремлюються у відповідних вузлах, і ставляться на місце відповідного піддерева в іншому дереві. На рисунку 3 представлене утворення нащадка методом обміну піддерев особин-батьків.

Рисунок 3 – Виконання оператора кросінговера й вузлової мутації

        Перед збереженням особин-нащадків, отриманих у результаті оператора кросінговера, необхідно перевіряти розмір нащадків, і з урахуванням цієї перевірки виконувати або скасовувати обмін.
        Мутація може бути вузлова (1%), що усікає (1%) і зростаюча (3%). Зростаючій мутації віддається перевага, тому що цей оператор має більші можливості [17]. При виконанні оператора мутації також буде перевірятися розмір особини, яка мутувала.
        Для формування нової популяції з поточного розширеного нащадками покоління застосовні 2 методи. Перший - елітарна схема, що полягає в копіюванні заданої кількості особин з найкращими значеннями фітнес-функції в наступну популяцію. Другий метод - пропорційний отбір, заснований на прямопропорціональності ймовірності вибору особини і її значень фітнес-функції.
        Принципова схема роботи алгоритму складається з наступних основних фаз (рисунок 4):

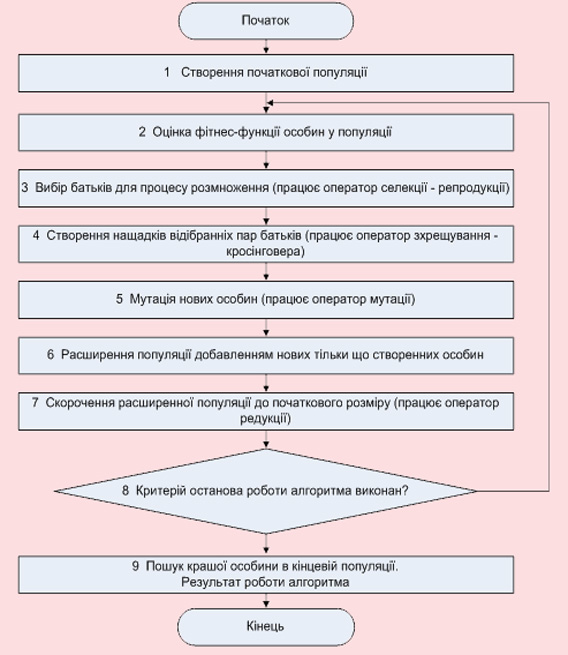
Рисунок 4 – Основні фази процесу еволюції рішень

        Програмна реалізація методу рішення задачі буде виконана в середовищі C++ Builder 6.0.

Висновки

        У магістрскій роботі запропоноване рішення актуальної наукової задачі - оптимізації параметрів коксування вугілля. Для одержання представлення про сучасний стан розробок по темі роботи був виконаний і відображений у роботі науковий пошук матеріалів. Увага приділялася моделям і методам моделювання й оптимізації процесу коксування вугілля з метою його оптимізації, а також інструментальним засобам, що дозволяють виконати апроксимацію по заданій вибірці даних.
        У результаті аналізу зібраної інформації були виявлені плюси й недоліки застосовуваних моделей, методів і програмних засобів і визначений напрямок власних досліджень. Розроблено математичну постановку задачі, обраний метод рішення - метод символьної регресії генетичного програмування. Для методу рішення визначені параметри: кодування рішень, проблемно-орієнтовані оператори кросінговера й мутації, функція оцінки придатності потенційного рішення.
        Подальша робота полягає в реалізації запропонованого методу рішення даної задачі, визначенні найбільш ефективних значень параметрів алгоритму, перевірці адекватності побудованої моделі, визначенні оптимальних значень параметрів шихти для одержання якісного коксу.

Література

        1. Шубеко П.З. Непрерывный процесс коксования / П.З. Шубеко, Г.И. Еник – М.: “Металлургия”, 1974. – 224 c.
        2. Иванов Е.Б. Технология производства кокса / Е.Б. Иванов, Д.А. Мучник – «Вища школа», 1976. – 232 c. – 71-74, 105-112 c.
        3. Кауфман А.А. Теория и практика современных процессов коксования: cборник примеров и задач / А.А. Кауфман, В.Д. Глянченко, С.А. Косорогов – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 61 c. – 11-19 c.
        4. Реакционная способность кокса и методы ее регулирования: материалы междунар. науч. конф. [«Химия, химическая технология и биотехнология на рубеже тысячелетий»], (Томск 11-16 сент. 2006 г.) – Томский гос. политех. ун-т, 2006. – 51 с. – с. 11-16с.
        5. Гребенюк А.Ф. Расчеты процессов коксового производства / А.Ф. Гребенюк, А.И Збыковский. – Донецк, 2008 – 188 с.
        6. Оптимизация качества каменноугольного пека в условиях ОАО “Авдеевский коксохимический завод”: научно-практ. конф. ["Донбасс 2020: наука и техника - производству"], (Донецк 5-6 фев. 2002 г.) – Д: Донецкий нац. тех. ун-т, 2002.
        7. Крыштановский А.О. Ограничения метода регрессионного анализа / А.О. Крыштановский // Социология – Режим доступа к журн.: http://socioline.ru/node/529.
        8. Моделирование тепловых свойств кокса: сб. трудов международ. науч. конф. [«Математические методы в технике и технологиях»] – Кострома: КГУ, 2004. - Т.1.
        9. Грешилов А.А. Математические методы построения прогнозов / А.А. Грешилов , В.А. Стакун, А.А. Стакун – Москва, 1997. – 106 с. – с. 28-29, 91-93.
        10. Dispulus : программ. продукт [Электронный ресурс]. – Режим доступа: http://www.rmltech.com/.
        11. DTREG: программ. продукт [Электронный ресурс]. – Режим доступа: http://www.dtreg.com/index.htm.
        12. Deductor 5: программ. продукт [Электронный ресурс]. – Режим доступа: http://www.basegroup.ru/.
        13. Мучник Д.А. Расчеты и прогнозирование показателей качества металлургического кокса с использованием ПК: учебное пособие / Д.А. Мучник, В.М. Гуляев – Днепродзержинск, 2007. – 225 с.
        14. AtteStat: программ. продукт [Электронный ресурс]. – Режим доступа: http://attestatsoft.com/download.htm.
        15. Genetic Programming: An Introduction / W. Banzhaf, P. Nordin, R. Keller, F. Francone. – San Francisco, 1998.
        16. Koza J. R. Genetic Programming: On the Programming of Computers by Means of Natural Selection / J. R. Koza. – MIT Press, Cambridge, 1992.
        17. Скобцов Ю.А. Основы эволюционных вычислений: учебное пособие для вузов/ Ю.А. Скобцов. – Донецкий нац. техн. ун-т. – Донецк: ДонНТУ, 2008.
        18. Zelinka I. Symbolic regression – an overview / I. Zelinka. – Tomas Bata University Zlin, 2002.

        Догори