Development of MIMD-simulator for researching of automated network objects with lumped
prof. V.A. Svjatnyj
Introduction
Network objects are widely-distributed in many areas of technology as objects for research, design, automation, control, etc. Network objects are complicated and critical for security and reliability dynamic systems. Not many problems can be solved analytically. Therefore simulation of object is important by working and design.
Urgent problem of computational mathematics is the development of parallel methods and algorithms for solving equations of network dynamic objects.
Here will be analyzed the development of parallel simulation for automated network object. The network object here is the mine ventilation network.
Automation in mine ventilation networks acting as regulators, which are situated in some branches of mine. With these regulators is done control of air flow occurs in network.
The formal description of the ANDO with lumped parameters.
Topological description
Graph of network object is created automatically. Graph of mine ventilation network is represented on Pic. 1.1. Qi — air flow, Ri — aerodynamic resistance. [2]
Branches in Q2, Q6, Q8, Q10 and Q11 have automated control.

Pic 1.1 – Graph of mine ventilation network
Mathematical description of air-dynamic system
Lumped parameter model allows for various research tasks required accuracy. Network object
considered as a graph G (n, m), with n = |U| nodes and m = |Q|
branches.
For acquisition of mathematical models with lumped parameters must be done the following steps:
From Table 1.1 is acquisitioned incidence matrix, which
clearly show the connections between nodes and branches of network, and
units matrix:
А = FА(AKJ, EKK, Qi) (1)
S = FS(AKJ, EKK, QI) (2),
where FA and FS — algorithms, which are generated by these
matrix.
Differential equations for branch Qi is the following
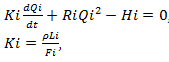 (3)
(3)
Emerging air flow vector Q, vector H and diagonal matrix of parameters K and R
Qi = (X,Y) (4)
H = (Hx,Hy) (5)
![]() (6)
(6)
![]() (7)
(7)
X and Y — are the air flow in a tree and antitree branches of graph
Thus, in the form of a matrix differential equation looks like:
 (8)
(8)
Getting a model suitable for simulation
A system of differential equations (8) is already a model. But tis model is not intended to calculating with computer. It must be leaded to such a form that it can be solved using a numerical method.
To bring the equations into proper form:
- Elements of incidence matrix A = (AxAy) and vector Q = (X, Y) substituted for the second equation in system of differential equations (8), and received:
- Find for Matrix Ax a return matrix. Then
- Convert contour equation, solving their relatively to vector derivatives
- Substitute to the first equation (14) the second and obtained the following system
- Find inverse matrix w1
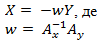 (13)
(13)
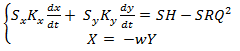 (14)
(14)
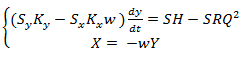 (15)
(15)
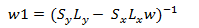 (16)
(16)
and accordingly:
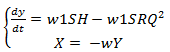 (17)
(17)
If Sp = w1S,
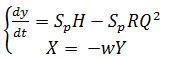 (18)
(18)
Thus, the resulting system of equations (18) is a simulation model, which can be solved using numerical methods on computer.
Problem-aided modeling ANDO
Methods and tools for modeling NDO
Solving differential equations using numerical methods — it is one of the most important tasks of scientific calculations. Because of the size of systems of equations there are special demands to algorithms and architectures of computers. [1] For a network of mine ventilation this solution is the value of air flows Qi in branches.
For numerical simulation was chosen Linear multistep method. Linear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point.
It is needed to find an approximate solution of
differential equation ![]() (19)
(19)
satisfying the initial conditions
![]() (20)
(20)
Two-step (or second order) algorithm is follows:
![]() (21)
(21)
The system of equations (18) can be represented as
 (22)
(22)
Tasks of research and development
Requirements of modeling ANDO
Simulator is based on MIMD Architecture (for Flynn's classification) — multiply instructions — multiply dates. This architecture is a multiprocessor and running asynchronously. At any time, different processors can perform different instructions on different pieces of data. Organization of MIMD machines can both with shared and with local memory.
For this simulator was chosen MIMD with the shared memory.
Level parallelization is elected so that one regulator relates to one processor. Thus, number of processors will match the number of regulators in network.
The structure also includes a CCM simulator — control calculating machine. The task of it is to monitor the processes that occurring in the ventilation mines, and if necessary, control regulators to raise or reduce air flows.
References
- Научные труда Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП – 2008). Выпуск 7(150): Донецк: ДонНТУ, 2008. – 290с.
- Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern
- Бройнль Т., Паралельне Програмування: — Початковий курс: Навч. Посібник. – К.:Наук.думка, 1997. – 358с.
- Святний В.А., Молдованова О.В., Перерва Л.О. Проблемно орієнтоване паралельне моделююче середовище для динамічних мережних обє’ктів. – Наукові праці ДонДТУ, серія «ІКОТ», вип. 29, 2001. – C 246-253.
- Хьюз К., Хьюз Т. Параллельное и распределенное программирование на С++ / Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 672 с.: ил.
- Святний В.А. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія ІКОТ, вип. 6., 1999, с. 6-14.
- MPI: A Message-Passing Interface Standard [Электронный ресурс]. — Режим доступа: http://www.mpi-forum.org/docs/mpi-11-html/mpi-report.html

