Розробка MIMD-симулятора для дослідження автоматизованих мережевих об’єктів з зосередженими параметрами
Актуальність
Мережні об'єкти розповсюджені у багатьох галузях техніки як об'єкти для дослідження, проектування, автоматизації, керування, тощо. Мережні об'єкти належать до складних та критичних за безпекою й надійністю динамічних систем. Невелика кількість задач може бути вирішена аналітично. Тому засоби моделювання об'єкту при експлуатації та проектуванні мають велике значення.
Актуальною проблемою обчислювальної математики є розробка паралельних методів і алгоритмів для вирішування рівнянь мережних динамічних об’єктів.
Створення моделей дозволяє прогнозувати результат експерименту і знижувати кількість помилок, що робить значно меньшими витрати під час наукового і технологічного пошуку. Через топологічні складності об'єктів і значного обсягу обчислень завдання можуть бути вирішені в потрібні терміни тільки при використанні високопродуктивних паралельних систем.
Метп розробки та досліджень
Метою даної роботи є розробка та налагодження паралельного моделюючого середовища для моделювання автоматизованного мережевого динамічного об'єкта з зосередженими параметрами.
Вступ
У цій роботі буде виконаний аналіз розробки паралельних симуляторів для автоматизованого мережного об'єкту. В якості мережного об'єкту виступає шахтна вентиляційна мережа (ШВС).
Автоматизація у ШВМ виконуєтья за допомогою регуляторів. За допомогою цих регуляторів відбувається управління потоками повітря у мережі.
Формальний опис МДО з зосередженими параметрами.
Топологічне описання
Граф мережного об'єкту створюється автоматично. У табл. 1.1 зображене початкове кодування графа для ШВМ, граф якої відповідно зображений на рис. 1.1. Стовпці таблиці мають наступні найменування: AKJ – початковий вузел, EKK – кінцевий вузел, Qi – i-ий повітряний потік, Ri – аеродинамічний опір, Hi – перепад тиску між вузлами AKJ та EKK. [2]
У гілках Q2, Q6, Q8, Q10 та Q11 знаходяться автоматизовані регулятори.

Рисунок 1.1 – Граф шахтної вентиляційної мережі
Таблиця 1.1 – Початкове кодування графа
|
AKJ |
EKK |
Qi |
Ri |
Ki |
Hi |
Коментар |
|
1 |
2 |
Q3 |
R3 |
K3 |
0 |
Відкаточний штрек |
|
1 |
3 |
Q2 |
R2 |
K2 |
0 |
Відкаточний штрек |
|
1 |
6 |
Q4 |
R4 |
K4 |
0 |
Відкаточний штрек |
|
1 |
7 |
Q5 |
R5 |
K5 |
0 |
Відкаточний штрек |
|
2 |
3 |
Q6 |
R6 |
K6 |
0 |
Повітропровід |
|
2 |
4 |
Q8 |
R8 |
K8 |
0 |
Повітропровід |
|
3 |
4 |
Q7 |
R7 |
K7 |
0 |
Повітропровід |
|
4 |
5 |
Q12 |
R12 |
K12 |
0 |
Вентиляційний штрек |
|
5 |
1 |
Q1 |
R1 |
K1 |
H1 |
Вентилятор |
|
6 |
8 |
Q10 |
R10 |
K10 |
0 |
Повітропровід |
|
7 |
8 |
Q11 |
R11 |
K11 |
0 |
Повітропровід |
|
8 |
5 |
Q13 |
R13 |
K13 |
0 |
Вентиляційний штрек |
Математичне описання аеро-динамічної системи
Модель з зосередженими параметрами дає для різноманітних дослідницьких завдань потрібну точність.
Мережевий об'єкт розглядається як граф G(n,m), з n = |U| вузлів та m = |Q| гілок.
Він кодується таким же чином, як було зазначено у попередньому розділі (табл. 1.1 та рис. 1.1).
Для отримання математичного описання моделі з зосередженими параметрами потрібно виконати наступні
кроки:
З таблиці 1.1 отримуються матриця інціденцій, яка однозначно відтворює зв’язки між вузлами та гілками
мереж та матриця контурів:
А = FА(AKJ, EKK, Qi) (1)
S = FS(AKJ, EKK, QI) (2),
де FA та FS – алгоритми, за якими генеруються ці матриці.
Диференціальне рівняння для гілки Qi має наступний вигляд
 (3)
(3)
Формуються вектор повітряних потоків Q, вектор перепадів тиску H та діагональні матриці параметрів K та R
Qi = (X,Y) (4)
H = (Hx,Hy) (5)
![]() (6)
(6)
![]() (7)
(7)
X та Y – це повітряні потоки у гілках дерева та антидерева графа відповідно.
У матричному вигляді диференціальні рівняння мають вигляд:
 (8)
(8)
Рішення отриманої системи (8) може використовуватися для багатьох завдань, таких як дослідження розподілення повітряних потоків за заданою топологією, спостереження за зміною цього розподілення при зміні параметрів та топології мережевого об'єкту та інші.
Структура багатозв'язаної системи автоматизованого керування потоками повітря в гілках МДО. Математичний опис системи
Задача автоматизованого керування повітрям в ШВМ є актуальною, тому що навіть наявність потужних вентиляторів не завжди забезпечує безпечний режим провітрювання. Безпечний режим може бути досягнутий автоматичним керуванням процесами повітряросподілення. Існує два способи керування цими процесами: використання вентиляторів з регуляторами та регуляторів, які знаходяться саме у вихідних струменях.
Вентилятори з H-регуляторами
Такі вентилятори мають аеродинамічні характеристики, які можуть бути апроксимовані за наступною формулою [2]:
![]() (9)
(9)
HiN автоматично регулюється за кількістю обертів електродвигунів вентилятора.
 (10)
(10)
Регулятори повітряних потоків
Схема вентиляції дільниці включає до свого складу регулятори повітряних потоків, які підтримують заданий повітряний потік Qsoll. Кожне рівняння для регуляторів може бути представлено за допомогою диференціальних та алгебраїчних рівнянь [2].
 (11)
(11)
Отримання моделі, придатної до симуляції
Система диференційних рівнянь (8) вже є модель. Але така модель не призначена для вирішення на обчислюючий машині. ЇЇ потрібно привести до такої форми, щоб вона могла бути вирішена за допомогою одного з чисельних методів.
Для приведення системи рівнянь до належної форми потрібно:
- Елементи матриці інциденцій А=(АxAy) та вектору Q=(X,Y) підставити до другого рівняння в системі диференційних рівнянь (8), та отримується:
- До матриці Ax знайти зворотню матрицю. Тоді,
- Перетворити рівняння контурів, вирішуючи їх відносно векторів похідних
- Підставити до першого рівняння системи (14) друге, отримати наступну систему
- Знайти зворотню матрицю w1
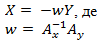 (13)
(13)
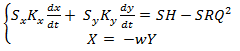 (14)
(14)
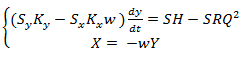 (15)
(15)
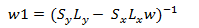 (16)
(16)
і відповідно:
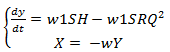 (17)
(17)
Якщо Sp = w1S,
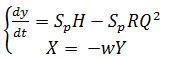 (18)
(18)
Таким чином, отримана система рівнянь (18) є моделю, придатною для вирішення на обчислюючій машині за допомогою чисельних методів.
Постановка задачі моделювання автоматизованого МДО
Задачею даного симулятора є моделювання автоматизованого мережного динамічного об'єкту, а саме автоматизованої ШВМ.
Поставлені цілі:
- Моделювання реальних автоматизованих ШВМ
- Моделювання роботи регуляторів при зміненні параметрів
- Реалізація паралельної моделі автоматизованих мережевих об'єктів (АМДО)
- Реалізація та дослідження паралельного симулятора АМДО
Методи та засоби моделювання МДО
Вирішення диференціальних рівнянь за допомогою чисельних методів – це одна з найважливіших задач наукових розрахунків і через розмір систем рівнянь ставить особливі вимоги як до алгоритмів, так і до архітектур обчислювальних машин. Для вирішення рівнянь вибирається певний чисельний метод, що у результаті дає отримане рішення. [1] Для ШВМ – це рішення є значенням потоків повітря, що установились, Qi в і-их гілках.
Існує багато різноманітних чисельних методів для вирішення диференційних рівнянь. Вони різняться за точністю та складністю розрахунків.
Для симулятора був обраний чисельний метод Адамса-Башфорта. Це різницевий метод чисельного інтегрування звичайних диференційних рівнянь, що дозволяє виліковувати таблицю наближених значень рішень у початкових точках.
Нехай потребується знайти наближене рішення диференційного рівняння
![]() (19)
(19)
що задовольняє початковій умові
![]() (20)
(20)
Чисельне рішення задачі полягає у побудуванні наближеного значення y1 рішення рівняння y(x) в точці x1 = x0 + h, де h – це шаг. Методами Адамса-Башфорта називають групу багатокрокових методів, в яких наближене рішення yn+1 = y(xn+1) в точці x n+1 = x0 + h(n+1) розраховується за формулою, що використовує поліном P(x)=Pkn(x). Методи Адамса k-го порядку потребують попереднього розрахування рішення в k початкових точках.
Цей алгоритм характеризується достатньою точністю.
Двухкроковий (або другого порядку) алгоритм Адамса-Башфорта має наступний вигляд:
![]() (21)
(21)
Система рівнянь (18) може бути представлена як
 (22)
(22)
Задачі розробок та досліджень
Вимоги до засобів моделювання АМДО
Ставляться наступні вимоги до засобів моделювання:
- Модель повинна відображати динамічні процеси реальних мереж
- Модель повинна включати до себе керуючу обчислювальну машину, яка керує регуляторами та перерозподіляє повітряні потоки
- Модельний опис та зображення результатів повинні мати інтуїтивно-зрозумілий інтерфейс
- Необхідно виконати симулятор таким чином, щоб робота, що виконується людьми, була зведена до мінімальної. Ця вимога обумовлюється можливою складністю динамічного мережного об'єкту. До цього входять також розподіл гілок на дерево та антидерево, формування матриць інціденцій та контурів.
- Імітація рішення проблем у режимі реального часу
- Високорозвинена система візуалізації та інтерфейс з користувачем.
Вимоги до засобів моделювання АМДО
Архітектура, на якій будується симулятор – це MIMD (за класифікацією Флінна) – multiply instructions – multiply dates. Ця архітектура є багатопроцесорною, працює асинхронно та незалежно. У будь-який час, різні процесори можуть виконувати різні інструкції над різними частинами даних. Організація MIMD машини може бути як із загальною, так і з розподіленою пам’яттю. Ця класифікація базується на тому, як процесори звертаються до пам'яті.
Для даного симулятору була обрана архітектура з загальною пам'яттю. З такою організацією всі процесори з'єднані з глобально-доступною пам’яттю.
Рівень розпаралелювання обирається таким чином, щоб одному регулятору ставилось у відповідність один процесор. Таким чином, кількість процесорів буде відповідати кількості регуляторів у мережі.
До структури симулятора також входить КОМ – керуюча обчислююча машина. Її задача – слідкувати за процесами, що відбуваються у вентиляції шахт, та у випадку необхідності, керувати регуляторами для підвищення або зменшення повітряних потоків.
Висновки
Архітектурою симулятору є MIMD із загальною пам’яттю. Паралелізація проходить на рівні регулятор-процессор.
Чисельним метод для вирішення диференціальних рівнянь обраний двухкроковий метод Адамса-Башфорта.
Такий MIMD-симулятор буде корисний для дослідження автоматизованих ШВМ, для моделювання критичних ситуацій та дослідження наслідків (для подальшого застереження можливих негативних результатів).
Використана література
- Научные труда Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП – 2008). Выпуск 7(150): Донецк: ДонНТУ, 2008. – 290с.
- Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern
- Бройнль Т., Паралельне Програмування: — Початковий курс: Навч. Посібник. – К.:Наук.думка, 1997. – 358с.
- Святний В.А., Молдованова О.В., Перерва Л.О. Проблемно орієнтоване паралельне моделююче середовище для динамічних мережних обє’ктів. – Наукові праці ДонДТУ, серія «ІКОТ», вип. 29, 2001. – C 246-253.
- Хьюз К., Хьюз Т. Параллельное и распределенное программирование на С++ / Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 672 с.: ил.
- Святний В.А. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія ІКОТ, вип. 6., 1999, с. 6-14.
- MPI: A Message-Passing Interface Standard [Электронный ресурс]. — Режим доступа: http://www.mpi-forum.org/docs/mpi-11-html/mpi-report.html
- B. Parhami, Introduction to Parallel Processing: Algorithms and Architectures, Plenum, New York, 1999.
- PD Dr.-Ing. Peter Sobe, Parallelrechnersysteme: Kapitel 3 - Parallelrechner Architekturen, Institute of Computer Engineering University of Lubeck, Germany, Parallelrechnersysteme WS 2009/2010
- Peter Rechenberg, Gustav Pomberger, Informatik-Handbuch 4., aktualisierte und erweiterte Auflage

