Разработка параллельного MIMD-симулятора для исследования автоматизированных сетевых объектов с сосредоточенными параметрами
Актуальность
Сетевые объекты распространены во многих отраслях техники как объекты для исследования, проектирования, автоматизации, управления и т.д. Сетевые объекты принадлежат к сложным и критическим по безопасности и надежности динамическим системам. Только небольшое количество задач может быть решено аналитически. Поэтому средства моделирования объекта при эксплуатации и проектировании имеют большое значение.
Создание моделей позволяет прогнозировать результат эксперимента и снижать количество ошибок, что значительно снижает затраты во время научного и технологического поиска. Из-за топологической сложности объектов и значительного объема вычислений задачи могут быть решены в приемлемые сроки только при использовании высокопроизводительных параллельных систем.
Цель разработки и исследований
Целью данной работы является разработка и отладка параллельной моделирующей среды для моделирования автоматичированного сетевого динамического объекта с сосредоточенными параметрами.
Вступление
В этой работе будет выполнен анализ разработки параллельных симуляторов для автоматизированного сетевого объекта. В качестве сетевого объекта выступает шахтная вентиляционная сеть (ШВС).
Автоматизация в сетях вентиляции шахты выступает в качестве регуляторов, находящихся в некоторых ветвях шахты. С помощью этих регуляторов происходит управление потоками воздуха в сети.
Формальное описание МДО с сосредоточенными параметрами.
Топологическое описание
Граф сетевого объекта создается автоматически. В табл. 1.1 изображено начальное кодирования графа для шахтной вентиляционной сети (граф на рис. 1.1). Столбцы таблицы имеют следующие наименования: AKJ — начальный узел, EKK — конечный узел, Qi — i-ый воздушный поток, Ri — аэродинамическое сопротивление, Hi - депрессия возможного активного элемента в і-й ветви. [2]
В ветвях Q2, Q6, Q8, Q10 и Q11 находятся автоматизированные регуляторы.

Рисунок 1.1 – Граф шахтной вентиляцийнной сети
Таблица 1.1 – Начальное кодирование графа
|
AKJ |
EKK |
Qi |
Ri |
Ki |
Hi |
Комментарий |
|
1 |
2 |
Q3 |
R3 |
K3 |
0 |
Откаточный штрек |
|
1 |
3 |
Q2 |
R2 |
K2 |
0 |
Откаточный штрек |
|
1 |
6 |
Q4 |
R4 |
K4 |
0 |
Откаточный штрек |
|
1 |
7 |
Q5 |
R5 |
K5 |
0 |
Откаточный штрек |
|
2 |
3 |
Q6 |
R6 |
K6 |
0 |
Воздухопровод |
|
2 |
4 |
Q8 |
R8 |
K8 |
0 |
Воздухопровод |
|
3 |
4 |
Q7 |
R7 |
K7 |
0 |
Воздухопровод |
|
4 |
5 |
Q12 |
R12 |
K12 |
0 |
Вентиляционный штрек |
|
5 |
1 |
Q1 |
R1 |
K1 |
H1 |
Вентилятор |
|
6 |
8 |
Q10 |
R10 |
K10 |
0 |
Воздухопровод |
|
7 |
8 |
Q11 |
R11 |
K11 |
0 |
Воздухопровод |
|
8 |
5 |
Q13 |
R13 |
K13 |
0 |
Вентиляцийнный штрек |
Математическое описание аэро-динамической системы
Модель с сосредоточенными параметрами дает для разных исследовательских задач нужную точность.
Сетевой объект рассматривается как граф G (n, m), с n = | U | узлов и m = | Q | ветвей.
Он кодируется так же, как было отмечено ранее (табл. 1.1 и рис. 1.1).
Для получения математического описания модели с сосредоточенными параметрами необходимо выполнить
следующие шаги:
Из таблицы 1.1 получается матрица инциденций, которая однозначно воспроизводит связи между узлами
и ветвями сетей, и матрица контуров:
А = FА(AKJ, EKK, Qi) (1)
S = FS(AKJ, EKK, QI) (2),
где FA и FS - алгоритмы, по которым генерируются эти матрицы.
Дифференциальное уравнение для ветки Qi имеет следующий вид
 (3)
(3)
Формируются вектор воздушных потоков Q, вектор депрессий H и диагональные матрицы параметров K и R
Qi = (X,Y) (4)
H = (Hx,Hy) (5)
![]() (6)
(6)
![]() (7)
(7)
X и Y - это воздушные потоки в дереве и антидереве графа ветвей.
Таким образом, в матричном виде дифференциальные уравнения имеют вид:
 (8)
(8)
Решение полученной системы (8) может использоваться для многих задач, таких как исследование распределения воздушных потоков по заданной топологии, наблюдение за изменением этого распределения при изменении параметров и топологии сетевого объекта и другие.
Структура многосвязанной системы автоматизованного управления потоками воздуха в ветвях СДО. Математическое описание системы
Задача автоматизированного управления воздухом в шахтах является актуальной, так как даже наличие мощных вентиляторов не всегда обеспечивает безопасный режим проветривания. Безопасный режим может быть достигнут автоматическим управлением процессами воздухораспределения. Существует два способа управления этими процессами: использование вентиляторов с регуляторами и регуляторов, которые находятся именно в вытяжках.
Вентиляторы с H-регуляторами
Такие вентиляторы имеют аэродинамические характеристики, которые могут быть аппроксимированны по следующей формуле [2]:
![]() (9)
(9)
HiN автоматически регулируется по количеству оборотов электромоторов вентилятора.
 (10)
(10)
Регуляторы воздушных потоков
Схема вентиляции участка включает в свой состав регуляторы воздушных потоков, которые поддерживают заданный воздушный поток Qзад. Каждое уравнение для регуляторов может быть представлено с помощью дифференциальных и алгебраических уравнений [2]
 (11)
(11)
Получение модели, пригодной для симуляции
Полученная система дифференциальных уравнений (8) уже есть модель. Но такая модель не предназначена для решения на вычислительной машине. Ее нужно привести к такой форме, чтобы она могла быть решена с помощью одного из численных методов.
Для приведения системы уравнений к надлежащей формы нужно:
- Элементы матрицы инциденций А = (АxAy) и вектора Q = (X, Y) подставляются во второе уравнение в системе дифференциальных уравнений (8), и получается:
- К матрице Ax находится обратная матрица. Тогда,
- Преобразовать уравнение контуров, решая их относительно векторов производных
- Подставив в первое уравнение системы (14) второе, получается следующая система
- Находится обратная матрица w1
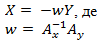 (13)
(13)
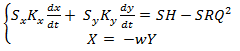 (14)
(14)
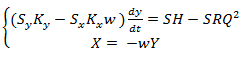 (15)
(15)
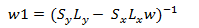 (16)
(16)
и соответственно:
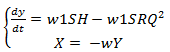 (17)
(17)
Если Sp = w1S,
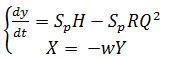 (18)
(18)
Таким образом, полученная система уравнений (18) является моделью, пригодной для решения с помощью численных методов.
Постановка задачи моделирования автоматизированного МДО
Задачей данного симулятора является моделирование автоматизированного сетевого динамического объекта, а именно автоматизированной сети шахтной вентиляции.
Поставленные цели:
- Моделирование реальных автоматизированных шахтных вентиляционных сетей
- Моделирование работы регуляторов при изменении параметров
- Реализация параллельной модели автоматизированных сетевых объектов (АМДО)
- Реализация и исследование параллельного симулятора АМДО
Методы и средства моделирования МДО
Была получена симуляционной модель, представленная системой дифференциальных уравнений.
Решение дифференциальных уравнений с помощью численных методов - это одна из важнейших задач научных расчетов и по размеру систем уравнений предъявляет особые требования как к алгоритмам, так и к архитектурам вычислительных машин. Для решения уравнений выбирается определенный численный метод, который в результате дает решение. [1] Для ШВС - это решение значения постоянных потоков воздуха Qi в і-ых ветках.
Существует много различных численных методов для решения дифференциальных уравнений. Они отличаются по степени точности и сложности расчетов.
Для симулятора был избран численный метод Адамса-Башфорта. Это разностный метод численного интегрирования обыкновенных дифференциальных уравнений, позволяет высчитывать таблицу приближенных значений решений в начальных точках.
Пусть требуется найти приближенное решение дифференциального уравнения
![]() (19)
(19)
удовлетворяющее начальному условию
![]() (20)
(20)
Численное решение задачи состоит в построении приближенного значения y1 решение уравнения y (x) в точке x1 = x0 h, где h - это шаг. Методами Адамса-Башфорта называют группу многошаговых методов, в которых приближено решения yn 1 = y (xn 1) в точке x n 1 = x0 h (n 1) рассчитывается по формуле, использующей полином P (x) = Pkn (x). Методы Адамса k-го порядка требуют предварительного расчета решения в k начальных точках.
Этот алгоритм характеризуется достаточной точностью.
Двухшаговый (или второго порядка) алгоритм Адамса-Башфорта имеет следующий вид: ![]() (21)
(21)
Система уравнений (18) может быть представлена, как
 (22)
(22)
Задачи разработок и исследований
Требования к средствам моделирования АМДО
Ставятся следующие требования к средствам моделирования:
- Модель должна отражать динамические процессы по реальным сетям
- Модель должна включать в себя управляющую вычислительную машину, которая управляет регуляторами и перераспределяет воздушные потоки
- Модельное описание и изображение результатов должны иметь интуитивно понятный интерфейс
- Необходимо выполнить симулятор таким образом, чтобы работа, выполняемая людьми, была сведена к минимальной. Это требование объясняется возможной сложностью динамичного сетевого объекта. Это включает в себя также распределение ветвей на дерево и антидерево, формирование матриц инциденций и контуров идругие.
- Имитация решения проблем в режиме реального времени
- Высокоразвитая система визуализации и интерфейс с пользователем
Разработка структуры параллельного симулятора
Архитектура, на которой строится симулятор - это MIMD (по классификации Флинна) - multiply instructions - multiply dates. Эта архитектура является многопроцессорной, работает асинхронно и независимо. В любое время, разные процессоры могут выполнять различные инструкции над различными частями данных. Организация MIMD машины может быть как с общей, так и с распределенной памятью. Эта классификация основана на том, как процессоры обращаются к памяти.
Для данного симулятора была выбрана архитектура с общей памятью. С такой организацией все процессоры соединены с глобально-доступной памятью.
Уровень распараллеливания избирается таким образом, чтобы одному регулятору ставился в соответствие один процессор. Таким образом, количество процессоров будет соответствовать количеству регуляторов в сети.
В структуру симулятора также входит УВМ - управляющая вычисляя машина. Ее задача - следить за процессами, происходящими в вентиляции шахт, и в случае необходимости, управлять регуляторами для повышения или уменьшения воздушных потоков.
Выводы
Архитектура симулятора - MIMD с общей памятью. Параллелизации проходит на уровне регулятор-процессор.
Численным метод для решения дифференциальных уравнений избран двухшаговый метод Адамса-Башфорта
Такой MIMD-симулятор будет полезен для исследования автоматизированных сетей шахтной вентиляции, для моделирование критических ситуаций и исследование последствий (для дальнейшего уменьшения возможных негативных результатов)
Структура параллельной моделирующей среды изображена на рис.2

Рисунок 2. Структура параллельной моделирующей среды. Анимация 176х332х5 кадров.
Задержка между кадрами 0.5 сек. Размер 5.03 Кбайт
При написании данного автореферата магистерская работа еще не завершенаю Окончательное завершение: декабрь 2010 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Литература
- Научные труда Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП – 2008). Выпуск 7(150): Донецк: ДонНТУ, 2008. – 290с.
- Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern
- Бройнль Т., Паралельне Програмування: - Початковий курс: Навч. Посібник. – К.:Наук.думка, 1997. – 358с.
- Святний В.А., Молдованова О.В., Перерва Л.О. Проблемно орієнтоване паралельне моделююче середовище для динамічних мережних обє’ктів. – Наукові праці ДонДТУ, серія «ІКОТ», вип. 29, 2001. – C 246-253.
- Хьюз К., Хьюз Т. Параллельное и распределенное программирование на С++ / Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 672 с.: ил.
- Святний В.А. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія ІКОТ, вип. 6., 1999, с. 6-14.
- MPI: A Message-Passing Interface Standard [Электронный ресурс]. — Режим доступа: http://www.mpi-forum.org/docs/mpi-11-html/mpi-report.html
- B. Parhami, Introduction to Parallel Processing: Algorithms and Architectures, Plenum, New York, 1999.
- PD Dr.-Ing. Peter Sobe, Parallelrechnersysteme: Kapitel 3 - Parallelrechner Architekturen, Institute of Computer Engineering University of Lubeck, Germany, Parallelrechnersysteme WS 2009/2010
- Peter Rechenberg, Gustav Pomberger, Informatik-Handbuch 4., aktualisierte und erweiterte Auflage
- Yunan Hu, Olga I. Koroleva and Miroslav Krsti, Nonlinear control of mine ventilation networks

