Рис.1. Структурная схема кластера (анимация: объем — 49,3 КБ, количество кадров — 40, количество циклов повторения — 7, размер — 80x20)

Цель

Цель работы заключается в анализе эффективности параллельных вычислительных систем.

Задачи исследования

В настоящее время значительный вклад в решение проблем создания новых многопроцессорных архитектурных реализаций и оценки их эффективности вносят дискретные марковские модели, которые по сравнению с непрерывными, более точно отражают работу вычислительных систем. Подобные задачи обладают большой размерностью и не могут быть эффективно реализованы на однопроцессорных ЭВМ. Решением этой проблемы является распараллеливание алгоритма построения дискретных марковских моделей на несколько вычислительных модулей [1]. Итак, среди задач магистерской работы, можно выделить следующие:

• oбзор методов анализа вычислительных систем;
• разработка дискретной марковской модели функционирования параллельной вычислительной системы неоднородного кластера;
• разработка параллельного алгоритма расчета характеристик функционирования параллельной вычислительной системы;
• исследование эффективности вычислительной системы .

Планируемые практические результаты

В работе магистерской работе предполагаются следующие практические результаты:

• дискретная марковская модель неоднородного кластера;
• разработанный и реализованный параллельныйо алгоритм построения дискретной марковской модели неоднородного кластера.
• анализ эффективности работы кластерных систем подобного типа.
• исследование эффективности вычислительной системы.

Актуальность темы

В настоящее время существует большое количество задач, требующих применения мощных вычислительных систем, среди которых задачи моделирования работы систем массового обслуживания и управления, распределённых систем, сложные вычислительные задачи и др. Для решения таких задач всё шире используются кластеры, которые становятся общедоступными и относительно недорогими аппаратными платформами для высокопроизводительных вычислений. Кластер представляет собой множество компьютеров (узлов), соединенных между собой высокоскоростными каналами связи, а специальное программное обеспечение позволяет организовать параллельную работу узлов.

Однако эффективность применения кластерных систем в настоящее время наталкивается на целый ряд нерешённых проблем, касающихся как их программного обеспечения (языков, технологий и инструментальных сред параллельного программирования), так и собственно организации параллельных вычислений и эффективности их выполнения [2]. Объединение большого количества компьютеров в единый вычислительный комплекс породило такие задачи, как сбалансированность нагрузки, выявление узких мест в вычислительной системе, обеспечение заданного времени ответа при работе большого количества пользователей, выбор оборудования при максимальной производительности при ограниченной заданной стоимости и т.д [3].

В связи с большим количеством создаваемых параллельных вычислительных систем и, во многих случаях, неэффективным их использованием, работы в этом направлении требуют дальнейшего развития и не утрачивают своей актуальности.

Научная новизна

• разработка дискретной модели параллельной вычислительной системы с разделяемыми дисками для оценки эффективности его работы;
• разработка нового параллельного алгоритма реализации дискретной марковской модели параллельной вычислительной системы на решетке процессоров, получение основных характеристик распараллеливания.

Общие понятия

Вычислительная система (ВС) — совокупность взаимосвязанных и взаимодействующих процессоров или ЭВМ, периферийного оборудования и программного обеспечения, предназначенную для подготовки и решения задач пользователей. Отличительной особенностью ВС по отношению к ЭВМ является наличие в них нескольких вычислителей, реализующих параллельную обработку. Создание ВС преследует следующие основные цели: повышение производительности системы за счет ускорения процессов обработки данных, повышение надежности и достоверности вычислений, предоставление пользователям дополнительных сервисных услуг и т.д.

Параллелизм в вычислениях в значительной степени усложняет управление вычислительным процессом, использование технических и программных ресурсов. Эти функции выполняет операционная система ВС [4].

В настоящее время накоплен большой практический опыт в разработке и использовании ВС самого разнообразного применения. Эти системы очень сильно отличаются друг от друга своими возможностями и характеристиками. Различия наблюдаются уже на уровне структуры.

Структура ВС — это совокупность комплексируемых элементов и их связей. В качестве элементов ВС выступают отдельные ЭВМ и процессоры. В ВС, относящихся к классу больших систем, можно рассматривать структуры технических, программных средств, структуры управления и т.д.

Для эффективности функционирования кластерной системы требуется соответствие класса решаемых задач структуре, на которой производят вычисления.

Большое разнообразие структур ВС затрудняет их изучение. Поэтому их классифицируют с учетом их обобщенных характеристик. С этой целью вводится понятие архитектура системы.

Архитектура ВС — совокупность характеристик и параметров, определяющих функционально-логическую и структурную организацию системы. Понятие архитектуры охватывает общие принципы построения и функционирования, наиболее существенные для пользователей, которых больше интересуют возможности систем, а не детали их технического исполнения [5]. Поскольку ВС появились как параллельные системы, то и рассмотрим классификацию архитектур под этой точкой зрения.

Классификация вычислительных систем

Существует большое количество признаков, по которым классифицируют вычислительные системы:

• по целевому назначению и выполняемым функциям;
• по типам и числу ЭВМ или процессоров;
• по архитектуре системы;
• по режимам работы;
• по методам управления элементами системы;
• по степени разобщенности элементов вычислительной системы;
• и др.

Самая ранняя и наиболее известная классификация архитектур вычислительных систем была предложенная в 1966 году М.Флинном. Она базируется на понятии потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. На основе числа потоков команд и потоков данных Флинн выделяет четыре класса архитектур: SISD,MISD,SIMD,MIMD.

SISD (single instruction stream / single data stream) — одиночный поток команд и одиночный поток данных. В таких машинах есть только один поток команд, все команды обрабатываются последовательно друг за другом и каждая команда инициирует одну операцию с одним потоком данных.

SIMD (single instruction stream / multiple data stream) — одиночный поток команд и множественный поток данных. В архитектурах подобного рода сохраняется один поток команд, включающий, в отличие от предыдущего класса, векторные команды. Это позволяет выполнять одну арифметическую операцию сразу над многими данными — элементами вектора.

MISD (multiple instruction stream / single data stream) — множественный поток команд и одиночный поток данных. Определение подразумевает наличие в архитектуре многих процессоров, обрабатывающих один и тот же поток данных. Однако ни Флинн, ни другие специалисты в области архитектуры компьютеров до сих пор не смогли представить убедительный пример реально существующей вычислительной системы, построенной на данном принципе. Ряд исследователей относят конвейерные машины к данному классу, однако это не нашло окончательного признания в научном сообществе.

MIMD (multiple instruction stream / multiple data stream) — множественный поток команд и множественный поток данных. Этот класс предполагает, что в вычислительной системе есть несколько устройств обработки команд, объединенных в единый комплекс и работающих каждое со своим потоком команд и данных [6].

Одним из преимуществ разновидности MIMD-систем, кластерных систем, является построение высокопроизводительного вычислительного комплекса заданной конфигурации. Для эффективности функционирования кластерной системы требуется соответствие класса решаемых задач структуре, на которой производят вычисления [3].

Эффективность кластерных систем

Одним из примеров вычислительных систем с распределенной обработкой являются кластеры. Они обладают высокой производительностью и «живучестью» вычислительных ресурсов. Классификация кластерных систем по cовместному использованию одних и тех же дисков отдельными узлами является самой распространенной. Одной из основных проблем при построении ВС с распределенной обработкой является выработка рекомендации для рационального использования ресурсов этой сети. Эта задача возникает как при эксплуатации, так и при проектировании сети. Для эффективной эксплуатации кластерной системы необходимо построить её аналитическую модель и для каждого класса решаемых задач определить основные параметры вычислительной среды. Эти модели можно использовать и для оптимизации ВС на стадии проектирования [3].

Для исследования эффективности функционирования кластеров и выработки рекомендаций рационального использования ресурсов могут быть применены непрерывные или дискретные аналитические модели. Дискретная модель по сравнению с непрерывной – более точная. Однако анализ кластерных систем с помощью дискретных моделей при большом количестве решаемых задач на ЭВМ сопряжен с большими временными затратами, так как количество состояний дискретной марковской модели комбинаторно возрастает при увеличении количества задач. Для уменьшения временных затрат надо распараллелить алгоритм построения дискретной модели кластера и оценить трудоемкость этого алгоритма и характеристики результатов распараллеливания [7].

Модель неоднородного кластера с совместным использованием дискового пространства

В модели с разделяемыми дисками каждый узел в кластере имеет свою собственную память, все узлы совместно используют дисковую подсистему [8]. Такие узлы связаны высокоскоростным соединением для того, чтобы передавать регулярные контрольные сообщения. При отсутствии таких сообщений определяются неисправности в вычислительной системе. Узлы в кластере обращаются к дисковой подсистеме по системной шине.

Одна из разновидностей кластера с совместным использованием дискового пространства представлена его упрощенной моделью на рис. 2.

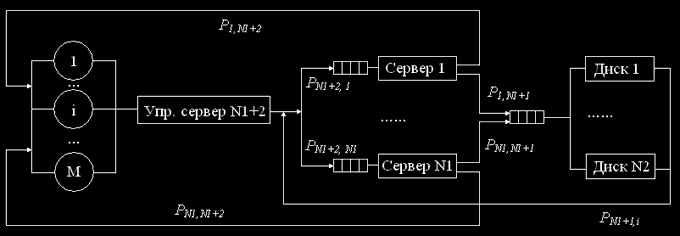
Рис.2. Структурная схема марковской модели неоднородного кластера с совместным использованием дискового пространства

Входной узел (управляющий сервер) распределяет между серверами приложений (выполняющими неодинаковые приложения) задачи. Количество серверов – приложений — N1. Каждый из них может обратиться к данным, расположенным на дисках, количество которых N2. Ввиду ограниченных вычислительных возможностей будем считать, что количество задач, обрабатываемое такой вычислительной системой не более М.

Построим дискретную марковскую модель. Так как дисковые накопители однородны, представим их многоканальным устройством.

Требования, поступающие на обслуживание на каждый из серверов, поступают в соответствующую ограниченную очередь (не более М), из которой на обслуживание выбираются по правилу «первый пришел – первый обслужился».

Кодирование состояний модели

Задачи, обрабатываемые на таком кластере, неоднородные имеют следующие характеристики:

• P_N1+2,i – вероятность запроса к i-му серверу, i=1..N1,
• P_i,N1+1 – вероятность запроса i-го сервера к одному из N2 дисков, i=1..N1,
• P_{i, N1+2} – вероятность завершения обслуживания задачи i-м сервером, i=1..N1,
• P_N1+1,i – вероятность завершения обслуживания задачи одним из N2 дисков и поступление на i-й сервер, i=1..N1,
• P_N1+2,0 – вероятность завершения обслуживания задачи,
• P_0,N1+2 – вероятность появления новой задачи.

Для вычислительных ресурсов примем, что длительности времен обслуживания заявок на входном узле, сервере приложений или дисковом массиве, соответственно, имеют геометрическое распределение со средним, равным T_i, (i=1..N1+2). Тогда

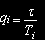– вероятность завершения обслуживания задачи на входном узле, сервере приложений или дисковом массиве, соответственно, (i=1..N1+2),

r_i – вероятность продолжения обслуживания задачи на входном узле, сервере приложений или дисковом массиве, соответственно, (i=1..N1+2), r_i=1-q_i.

Построение матрицы переходных вероятностей

За состояние системы примем размещение М заявок по N узлам 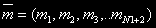, где m_i – количество задач в i-ом узле. Необходимо определить все возможные состояния. Обозначим множество состояний через 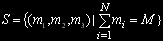. Число состояний системы для одного и того же количества задач j= 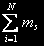равно числу размещений j задач по N узлам и определяется по формуле 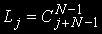, общее количество состояний вычисляется так:

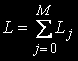
Вектор 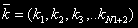определяет количество устройств в каждом узле ВС.

Расчет стационарных вероятностей

Для определения вектора стационарных вероятностей состояний 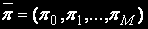необходимо решить систему линейных алгебраических уравнений (СЛАУ),

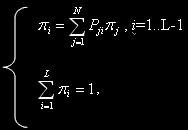
соответствующую рассмотренной модели кластера, где
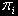— вероятность застать систему в i-м состоянии.

Расчет основных характеристик

Стационарные вероятности дают возможность определить средние значения временных характеристик обслуживания и занятости устройств вычислительной системы.

Для вычислений основных характеристик введем множество:

A_s = {l|0 =< m_s(l) < k_s},

где l € {1,L} номер состояния; s € {1,N} номер узла кластера.

Мощность этого множества обозначим . Множество A_s содержит номера тех состояний, для которых в s-м узле обработки находится менее k_s задач. Найдем среднее число занятых устройств в s-м узле обработки. Величина (k_s -m^l_s), l € A_s определяет число свободных устройств s-го узла в состоянии l. Среднее число свободных устройств в s-м узле вычисляется по формуле:

Среднее число занятых устройств в s-м узле определяется по формуле:

Загрузка устройств определяется по следующей формуле:

Среднее число задач, находящихся в s-м узле:

Среднее числo задач, находящихся в очереди к s-му узлу:

Среднее время пребывания в s-м узле:

Среднее время ожидания в s-м узле:

Среднее время пребывания в вычислительной системе:

Среднее время ожидания в вычислительной системе:

Распараллеливание задачи

Алгоритм состоит условно из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей.

Вычисление элемента матрицы переходных вероятностей не зависит от соседних элементов, следовательно, в основе параллельной реализации этой части параллельного алгоритма можно использовать принцип распараллеливания по данным [9].

В качестве базовой подзадачи можно взять расчет строки, столбца или блока матрицы переходных вероятностей. Это позволит сбалансировать загрузку вычислительных модулей кластера. Каждый процесс определяет, какие строки (столбцы, блоки) матрицы переходных вероятностей он должен вычислить и отправить управляющему процессу. Схема параллельного алгоритма приведена на рисунке 3.

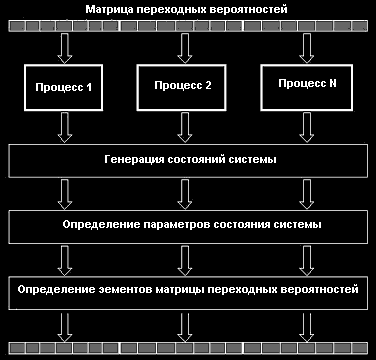
Рис.3. Параллельный алгоритм построения матрицы переходных вероятностей

Расчет стационарных вероятностей можно реализовать с использованием итерационного алгоритма, в котором в качестве базового используется алгоритм умножения матрицы на вектор. Схема алгоритма расчета вектора стационарных вероятностей представлена на рис.4. Для распараллеливания задачи умножения матриц можно использовать ленточную (по строкам, по столбцам) или блочную схему разделения данных.

При разделении данных по строкам для выполнения базовой подзадачи скалярного произведения матрицы на вектор процессор должен содержать соответствующую строку (столбец, блок) матрицы P={Pij} и копию вектора . После завершения вычислений каждая базовая подзадача определяет один из элементов вектора результата.

Для объединения результатов расчета и получения полного вектора, рассчитанных стационарных вероятностей, на каждом из процессоров вычислительной системы необходимо выполнить операцию обобщенного сбора данных, в которой каждый процессор передает свой вычисленный элемент вектора результата всем остальным процессорам [10].

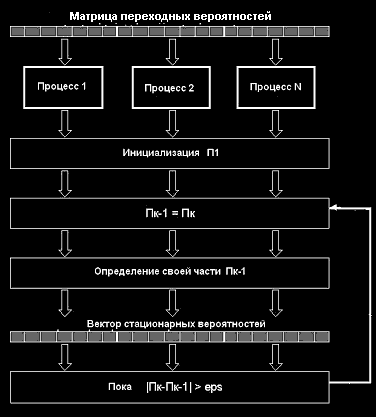
Рис.4. Параллельный алгоритм расчета вектора стационарных вероятностей

Выводы

В работе предложен параллельный алгоритм построения дискретной марковской модели неоднородного кластера. Предполагается анализ эффективности работы рассматриваемой параллельной вычислительной системы. Результаты моделирования могут быть использованы для повышения эффективности работы, для синтеза, анализа, реконфигурации кластерных систем подобного типа.

В дальнейшем этот алгоритм можно исследовать на параллельных структурах различной топологии.

Литература

1. Кучереносова О.В. Параллельный алгоритм построения дискретной марковской модели неоднородного кластера // Наукові праці Донецького національного технічного університету. — Донецьк, ДонНТУ, 2010.
2. Лю Лян. Исследование эффективности параллельных вычислений на кластере Московского энергетического института // Автореферат диссертации на соискание ученой степени к.т.н. — Москва, 2007.— 186 с. http://www.lib.ua-ru.net/diss/cont/296301.html
3. Михайлова Т.В. Повышение эффективности кластерных вычислительных систем на основе аналитических моделей. // Автореферат диссертации на соискание ученой степени к.т.н. — Донецк, 2007. — 20 с.
4. Воеводин Вл.В., Жуматий С.А. Вычислительное дело и кластерные системы. — Москва, 2007. — С. 79-91. — http://cluster.onu.edu.ua/docs/voevodin.pdf
5. Халабия Р.Ф. Организация вычислительных систем и сетей. — Москва, 2000. — С. 141 — http://window.edu.ru/window_catalog/pdf2txt?p_id=6623
6. Вл.В.Воеводин, А.П.Капитонова. Классификации архитектур вычислительных систем. — http://www.parallel.ru/computers/taxonomy/
7. Фельдман Л.П., Михайлова Т.В. Дискретная модель Маркова однородного кластера // Искусственный интеллект.— Донецк: ІПШІ МОН і НАН України «Наука і освіта», №3, 2006. — http://www.iai.dn.ua/public/JournalAI_2006_3/Razdel2/05_Fel%27dman_Mikhaylova.pdf
8. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя.— К.:«ДиаСофт», 1998. — 432 с.
9. Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. — http://www.nbuv.gov.ua/portal/natural/Npdntu/ikot/2009_10/09flppmm.pdf
10. Кучереносова О.В. Параллельный алгоритм построения дискретной марковской модели неоднородного кластера // Искусственный интеллект.— Донецк: ІПШІ МОН і НАН України “Наука і освіта”, 2010.

© Магистр ДонНТУ, Кучереносова Ольга Владимировна, 2010