«Дослідження ефективності паралельних обчислювальних систем»

Мал.1. Структурна схема кластера (анімація: об'єм — 49,3 КБ, кількість кадрів — 40, кількість циклів повторення — 7, розмір — 80x20)

Ціль

Ціль роботи полягає в аналізі ефективності паралельних обчислювальних систем.

Завдання дослідження

У цей час значний внесок у рішення проблем створення нових многопроцесорних архітектурних реалізацій й оцінки їхньої ефективності вносять дискретні марківскі моделі, які в порівнянні з безперервними, більш точно відбивають роботу обчислювальних систем. Подібні завдання мають велику розмірність і не можуть бути ефективно реалізовані на однопроцесорних ЕОМ. Рішенням цієї проблеми є розперелелювання алгоритму побудови дискретних марківських моделей на кілька обчислювальних модулів [1]. Отже, серед завдань магістерської роботи, можна виділити наступні:

oбзор методів аналізу обчислювальних систем;
розробка дискретної марківської моделі функціонування паралельної обчислювальної системи неоднорідного кластера;
розробка паралельного алгоритму розрахунку характеристик функціонування паралельної обчислювальної системи;
дослідження ефективності обчислювальної системи

Плановані практичні результати

У роботі магістерській роботі передбачаються наступні практичні результати:

дискретна марківська модель неоднорідного кластера;
розроблений і реалізований паралельний алгоритм побудови дискретної марківскої моделі неоднорідного кластера.
аналіз ефективності роботи кластерних систем подібного типу
дослідження ефективності обчислювальної системи

Актуальність теми

У цей час існує велика кількість задач, що вимагають застосування потужних обчислювальних систем, серед яких задачі моделювання роботи систем масового обслуговування й керування, розподілених систем, складні обчислювальні завдання й ін. Для рішення таких задач усе ширше використовуються кластери, які стають загальнодоступними й відносно недорогими апаратними платформами для високопродуктивних обчислень. Кластер являє собою набір комп'ютерів (вузлів), з'єднаних між собою високошвидкісними каналами зв'язку, а спеціальне програмне забезпечення дозволяє організувати паралельну роботу вузлів.

Однак ефективність застосування кластерних систем у цей час натрапляє на цілий ряд невирішених проблем, що стосуються як їхнього програмного забезпечення (мов, технологій й інструментальних середовищ паралельного програмування), так і власне організації паралельних обчислень й ефективності їхнього виконання [2]. Об'єднання великої кількості комп'ютерів у єдиний обчислювальний комплекс породило такі задачі, як збалансованість навантаження, виявлення вузьких місць в обчислювальній системі, забезпечення заданого часу відповіді при роботі великої кількості користувачів, вибір обладнання при максимальній продуктивності при обмеженій заданій вартості й т.д [3].

У зв'язку з великою кількістю створюваних паралельних обчислювальних систем й, у багатьох випадках, неефективним їхнім використанням, роботи в цьому напрямку вимагають подальшого розвитку й не втрачають своєї актуальності.

Наукова новизна

розробка дискретної моделі паралельної обчислювальної системи з поділюваними дисками для оцінки ефективності його роботи;
розробка нового паралельного алгоритму реалізації дискретної марківскої моделі паралельної обчислювальної системи на ґратах процесорів, одержання основних характеристик розпаралелювання.

Загальні поняття

Обчислювальна система (ОС) — сукупність взаємозалежних і взаємодіючих процесорів або ЕОМ, периферійного обладнання й програмного забезпечення, призначена для підготовки й рішення завдань користувачів. Відмінною рисою ОС стосовно ЕОМ є наявність у них декількох обчислювачів, що реалізують паралельну обробку. Створення обчислювальної системи переслідує наступні основні цілі: підвищення продуктивності системи за рахунок прискорення процесів обробки даних, підвищення надійності й вірогідності обчислень, надання користувачам додаткових сервісних послуг і т.д.

Паралелізм в обчисленнях у значній мірі ускладнює керування обчислювальним процесом, використання технічних і програмних ресурсів. Ці функції виконує операційна система ОС [4].

У цей час накопичений великий практичний досвід у розробці й використанні ОС найрізноманітнішого застосування. Ці системи дуже сильно відрізняються друг від друга своїми можливостями й характеристиками. Розходження спостерігаються вже на рівні структури.

Структура ОС — це сукупність елементів й їхніх зв'язків. Як елементи ОС виступають окремі ЕОМ і процесори. У ОС, що ставляться до класу більших систем, можна розглядати структури технічних, програмних засобів, структури керування й т.д.

Для ефективності функціонування кластерної системи необхідна відповідність класу розв'язуваних завдань структурі, на якій роблять обчислення.

Велика розмаїтість структур ОС утрудняє їхнє вивчення. Тому їх класифікують із урахуванням їхніх узагальнених характеристик. Із цією метою вводиться поняття архітектура системи.

Архітектура ОС — сукупність характеристик і параметрів, що визначають функціонально-логічну й структурну організацію системи. Поняття архітектури охоплює загальні принципи побудови й функціонування, найбільш істотні для користувачів, яких більше цікавлять можливості систем, а не деталі їхнього технічного виконання [5]. Оскільки ОС з'явилися як паралельні системи, то й розглянемо класифікацію архитектур під цієї точки зору.

Класифікація обчислювальних систем

Існує велика кількість ознак, по яких класифікують обчислювальні системи:

по цільовому призначенню й виконуваним функціям;
по типах і числу ЕОМ або процесорів;
по архітектурі системи;
по режимах роботи;
по методах керування елементами системи;
по ступені роз'єднаності елементів обчислювальної системи;
й ін.

Сама рання й найбільш відома класифікація архитектур обчислювальних систем була запропонована в 1966 році М.Флінном. Вона базується на понятті потоку, під яким розуміється послідовність елементів, команд або даних, оброблювана процесором. На основі числа потоків команд і потоків даних Флінн виділяє чотири класи архитектур: SISD, MISD, SIMD, MIMD.

SISD (single instruction stream / single data stream) — одиночний потік команд й одиночний потік даних. У таких машинах є тільки один потік команд, всі команди обробляються послідовно один за одним і кожною командою ініціює одну операцію з одним потоком даних.

SIMD (single instruction stream / multiple data stream) — одиночний потік команд і множинний потік даних. В архитектурах подібного роду зберігається один потік команд, що включає, на відміну від попереднього класу, векторні команди. Це дозволяє виконувати одну арифметичну операцію відразу над багатьма даними — елементами вектора.

MISD (multiple instruction stream / single data stream) — множинний потік команд й одиночний потік даних. Визначення має на увазі наявність в архітектурі багатьох процесорів, що обробляють той самий потік даних. Однак ні Флінн, ні інші фахівці в області архітектури комп'ютерів дотепер не змогли представити переконливий приклад реально існуючої обчислювальної системи, побудованої на даному принципі. Ряд дослідників відносять конвеєрні машини до даного класу, однак це не знайшло остаточного визнання в науковому співтоваристві.

MIMD (multiple instruction stream / multiple data stream) — множинний потік команд і множинний потік даних. Цей клас припускає, що в обчислювальній системі є кілька пристроїв обробки команд, об'єднаних у єдиний комплекс і працюючих кожне зі своїм потоком команд і даних [6].

Одним з переваг різновиду MIMD-систем, кластерних систем, є побудова високопродуктивного обчислювального комплексу заданої конфігурації. Для ефективності функціонування кластерної системи необхідна відповідність класу розв'язуваних завдань структурі, на якій виконують обчислення [3].

Ефективність кластерних систем

Одним із прикладів обчислювальних систем з розподіленою обробкою є кластери. Вони мають високу продуктивність й «живучістю» обчислювальних ресурсів. Класифікація кластерних систем з cумісного використання тих самих дисків окремими вузлами є найпоширенішою. Однієї з основних проблем при побудові ОС із розподіленою обробкою є вироблення рекомендації для раціонального використання ресурсів цієї мережі. Це завдання виникає як при експлуатації, так і при проектуванні мережі. Для ефективної експлуатації кластерної системи необхідно побудувати її аналітичну модель і для кожного класу розв'язуваних задач визначити основні параметри обчислювального середовища. Ці моделі можна використати й для оптимізації ОС на стадії проектування [3].

Для дослідження ефективності функціонування кластерів і вироблення рекомендацій раціонального використання ресурсів можуть бути застосовані безперервні або дискретні аналітичні моделі. Дискретна модель у порівнянні з непреривною — більш точна. Однак аналіз кластерних систем за допомогою дискретних моделей при великій кількості розв'язуваних задач на ЕОМ сполучений з більшими часовими витратами, тому що кількість станів дискретної марківскої моделі комбінаторно зростає при збільшенні кількості завдань. Для зменшення тимчасових витрат треба розпаралелити алгоритм побудови дискретної моделі кластера й оцінити трудомісткість цього алгоритму й характеристики результатів розпаралелювання [7].

Модель неоднорідного кластера зі спільним використанням дискового простору

У моделі з поділюваними дисками кожен вузел у кластері має свою власну пам'ять, всі вузли спільно використають дискову підсистему[8]. Такі вузли пов'язані високошвидкісним з'єднанням для того, щоб передавати регулярні контрольні повідомлення. При відсутності таких повідомлень визначаються несправності в обчислювальній системі. Вузли в кластері звертаються до дискової підсистеми по системній шині.

Один з різновидів кластера зі спільним використанням дискового простору представлена його спрощеною моделлю на мал. 2.

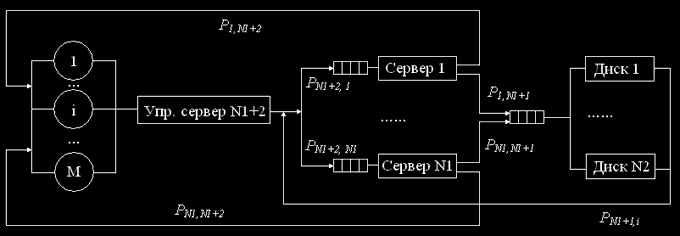
Структурна схема марківскої моделі неоднорідного кластера зі спільним використанням дискового простору

Мал.2. Структурна схема марківскої моделі неоднорідного кластера зі спільним використанням дискового простору

Вхідний вузел (керуючий сервер) розподіляє між серверами додатків (виконуючими неоднакові додатки) задачі. Кількість серверів-додатків — N1. Кожен з них може звернутися до даних, розташованим на дисках, кількість яких N2. Через обмежені обчислювальні можливості будемо вважати, що кількість задач, оброблювана такою обчислювальною системою не більше М.

Побудуємо дискретну марківску модель. Тому що дискові накопичувачі однорідні, представимо їх многоканальним пристроєм.

Вимоги, що надходять на обслуговування на кожний із серверів, надходять у відповідну обмежену чергу (не більше М), з якої на обслуговування вибираються за правилом «перший прийшов — перший обслужився».

Кодування станів моделі

Задачі, оброблювані на такому кластері, неоднорідні мають наступні характеристики:

P_N1+2,i — імовірність запиту до i-му сервера, i=1..N1,
P_i,N1+1 — імовірність запиту i-го сервера до одному з N2 дисків, i=1..N1,
P_{i, N1+2} — імовірність завершення обслуговування задачі i-м сервером, i=1..N1,
P_N1+1,i — імовірність завершення обслуговування задачі одним з N2 дисків і надходження на i-й сервер, i=1..N1,
P_N1+2,0 — імовірність завершення обслуговування задачі,
P_0,N1+2 — імовірність появи нового задачі

Для обчислювальних ресурсів приймемо, що тривалості часів обслуговування заявок на вхідному вузлі, сервері додатків або дисковому масиві, відповідно, мають геометричний розподіл із середнім, рівним T_i, (i=1..N1+2). Тоді

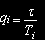— імовірність завершення обслуговування завдання на вхідному вузлі, сервері додатків або дисковому масиві, відповідно, (i=1..N1+2),

r_i — імовірність продовження обслуговування задачі на вхідному вузлі, сервері додатків або дисковому масиві, відповідно, (i=1..N1+2), r_i=1-q_i.

Побудова матриці перехідних імовірностей

За стан системи приймемо розміщення М заявок по N вузлах 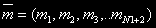, де m_i — кількість задач в i-ом вузлі. Необхідно визначити всі можливі стани. Позначимо безліч станів через 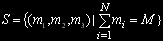. Число станів системи для того самого кількості завдань j= 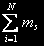дорівнює числу розміщень j задач по N вузлах і визначається по формулі 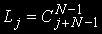, загальна кількість станів обчислюється так:

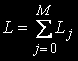
Вектор 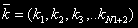визначає кількість пристроїв у кожному вузлі ОС.

Розрахунок стаціонарних імовірностей

Для визначення вектора стаціонарних імовірностей станів 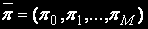необхідно вирішити систему лінійних алгебраїчних рівнянь (СЛАУ),

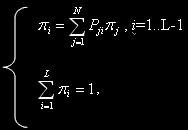
відповідної розглянутої моделі кластера, де
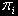— імовірність застати систему в i-м стані.

Розрахунок основних характеристик

Стаціонарні ймовірності дають можливість визначити середні значення тимчасових характеристик обслуговування й зайнятості пристроїв обчислювальної системи.

Для обчислень основних характеристик введемо множину:

A_s = {l|0 =< m_s(l) < k_s},

де l € {1,L} номер стану; s € {1,N} номер вузла кластера.

Потужність цієї множини позначимо . Множина A_s містить номери тих станів, для яких в s-м вузлі обробки перебуває менше k_s завдань. Знайдемо середнє число зайнятих пристроїв в s-м вузлі обробки. Величина (k_s-m^l_s), l € A_s визначає число вільних пристроїв s-го вузла в стані l. Середнє число вільних пристроїв в s-м вузлі обчислюється по формулі:

Середнє число зайнятих пристроїв в s-м вузлі визначається по формулі:

Завантаження пристроїв визначається по наступній формулі:

Середнє число задач, що перебувають в s-м вузлі:

Середнє числo задач, що перебувають у черзі до s-му вузла:

Середній час перебування в s-м вузлі:

Середній час очікування в s-м вузлі:

Середній час перебування в обчислювальній системі:

Середній час очікування в обчислювальній системі:

Розпаралелювання задачі

Алгоритм складається умовно із двох частин: обчисленя матриці перехідних імовірностей і вектора стаціонарних імовірностей.

Обчислення елемента матриці перехідних імовірностей не залежить від сусідніх елементів, отже, в основі паралельної реалізації цієї частини паралельного алгоритму можна використати принцип розпаралелювання по даним [9].

У якості базової підзадачі можна взяти розрахунок рядка, колонки або блока матриці перехідних імовірностей. Це дозволить збалансувати завантаження обчислювальних модулів кластера. Кожен процес визначає, які рядки (колонки, блоки) матриці перехідних імовірностей він повинен обчислити й відправити керуючому процесу. Схема паралельного алгоритму наведена на малюнку 3.

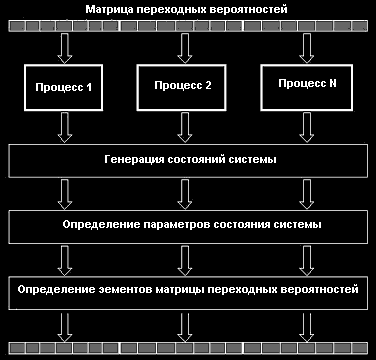
Паралельний алгоритм побудови матриці перехідних імовірностей

Мал. 3. Паралельний алгоритм побудови матриці перехідних імовірностей

Розрахунок стаціонарних імовірностей можна реалізувати з використанням ітераційного алгоритму, у якому в якості базового використається алгоритм множення матриці на вектор. Схема алгоритму розрахунку вектора стаціонарних імовірностей представлена на мал.4. Для распараллеливания завдання множення матриць можна використати стрічкову (по рядках, по стовпцях) або блокову схему поділу даних.

При поділі даних по рядках для виконання базової підзадачі скалярного добутку матриці на вектор процесор повинен містити відповідний рядок (колонка, блок) матриці P={Pij} і копію вектора . Після завершення обчислень кожна базова подзадача визначає один з елементів вектора результату.

Для об'єднання результатів розрахунку й одержання повного вектора, розрахованих стаціонарних імовірностей, на кожному із процесорів обчислювальної системи необхідно виконати операцію узагальненого збору даних, у якій кожен процесор передає свій обчислений елемент вектора результату всім іншим процесорам [10].

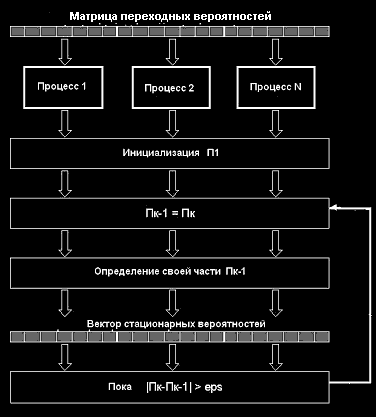
Паралельний алгоритм розрахунку вектора стаціонарних імовірностей

Мал.4. Паралельний алгоритм розрахунку вектора стаціонарних імовірностей

Висновки

У роботі запропонований паралельний алгоритм побудови дискретної маркіовскої моделі неоднорідного кластера. Передбачається аналіз ефективності роботи розглянутої паралельної обчислювальної системи. Результати моделювання можуть бути використані для підвищення ефективності роботи, для синтезу, аналізу, реконфігурації кластерних систем подібного типу.

Надалі цей алгоритм можна досліджувати на паралельних структурах різної топології.

Література

Кучереносова О.В. Параллельный алгоритм построения дискретной марковской модели неоднородного кластера // Наукові праці Донецького національного технічного університету. — Донецьк, ДонНТУ, 2010.
Лю Лян. Исследование эффективности параллельных вычислений на кластере Московского энергетического института // Автореферат диссертации на соискание ученой степени к.т.н. — Москва, 2007.— 186 с. http://www.lib.ua-ru.net/diss/cont/296301.html
Михайлова Т.В. Повышение эффективности кластерных вычислительных систем на основе аналитических моделей. // Автореферат диссертации на соискание ученой степени к.т.н. — Донецк, 2007. — 20 с.
Воеводин Вл.В., Жуматий С.А. Вычислительное дело и кластерные системы. — Москва, 2007. — С. 79-91. — http://cluster.onu.edu.ua/docs/voevodin.pdf
Халабия Р.Ф. Организация вычислительных систем и сетей. — Москва, 2000. — С. 141 — http://window.edu.ru/window_catalog/pdf2txt?p_id=6623
Вл.В.Воеводин, А.П.Капитонова. Классификации архитектур вычислительных систем. — http://www.parallel.ru/computers/taxonomy/
Фельдман Л.П., Михайлова Т.В. Дискретная модель Маркова однородного кластера // Искусственный интеллект.— Донецк: ІПШІ МОН і НАН України «Наука і освіта», №3, 2006. — http://www.iai.dn.ua/public/JournalAI_2006_3/Razdel2/05_Fel%27dman_Mikhaylova.pdf
Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя.— К.:«ДиаСофт», 1998. — 432 с.
Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. — http://www.nbuv.gov.ua/portal/natural/Npdntu/ikot/2009_10/09flppmm.pdf
Кучереносова О.В. Параллельный алгоритм построения дискретной марковской модели неоднородного кластера // Искусственный интеллект.— Донецк: ІПШІ МОН і НАН України “Наука і освіта”, 2010.