Fig. 1. The block claster diagramme (animation: volume — 49,3 KB, quantity of shots — 40, quantity of repetition cycles — 7, the size — 80x20)

The work purpose

The work purpose is to analyse the efficiency of parallel computing systems

Research problems

• the review of methods of the computing analysis systems;
• creating of the markow’s functioning models of the parallel computing system of the non-uniform claster;
• creation of calculation parallel algorithm of functioning parallel computing system characteristics;
• research of efficiency of the computing system.

Planned practical results

In magister’s the following practical results are expected:

• The discrete markow’s model of the non-uniform claster;
• developed and realised parallel algorithm of non-uniform discrete markows cluster construction;
• the overall performance cluster systems analysis.

Theme urgency

Now adways there is a considerable quantity of the problems demand with the application of powerful computing systems. For the decision of such problems clusters are starting to be used more and more widely. Association of a large quantity of computers in the one computer complex has caused such problems, as equation of loading, finding the bottlenecks in the computing system, maintenance of the server answer when working with a considerable quantity of users, an equipment choice with the maximum productivity at the limited cost, etc. [1].

Because of the large quantity of created parallel computing systems works in this area are still urgency.

Scientific novelty

• creating the parallel computing system with divided disks discrete model for an estimation of efficiency of its work;
• working out of discrete markow’s models of the parallel computing system new parallel algorithm of realisation on a lattice of processors, reception of the basic characteristics of parallelization.

Non-uniform cluster model with sharing of the disk space

In model with divided disks each knot in the cluster has it’s the own memory, also all knots share a disk subsystem [2].

One of cluster versions with disk sharing space is presented by its simplified model on fig. 2.

Fig. 2. The block markow’s claster model with sharing of disk space

Model conditions coding

The operating server distributes arriving problems on application servers. Quantity of application servers – N1, disks – N2. The problems processed on such cluster are non-uniform and have following characteristics:

• P_N1+2,i – inquiry probability to i server, i=1. N1,
• P_i,N1+1 – inquiry probability of i th server to one of N2 disks, i=1. N1,
• P_{i, N1+2} – end probability of service of a problem i-м a server, i=1. N1,
• P_N1+1,i – end probability of service of a problem one of N2 disks and receipt on i-й a server, i=1. N1,
• P_N1+2,0 – end probability of service of a problem,
• P_0,N1+2 – probability of occurrence of a new problem.

Construction of transitive probabilities matrix

Let's consider that the quantity of problems processed by such computing system is no more then M [3].

The number of conditions of system for the same quantity of problems is j = and is equal to number of placings j problems on N knots and is defined under the formula , the total of conditions is:

The vector defines the quantity of devices in each knot.

It is necessary to define a matrix of transitive probabilities P = {P_ij} LxL. Calculation of elements of a matrix directly depends on concrete structure of the computing system.

Stationary probabilities calculation

For definition of a stationary probabilities vector it is necessary to solve system of the linear algebraic equations (Slough),

corresponding to the considered claster model, where
— probability to find system in i-th condition.

Basic characteristics calculation

Stationary probabilities give the chance to define average values of service and employment of the computing system devices time characteristics.

The average number of the occupied devices in s-th knot is defined by the formula:

Loading of devices is defined by the following formula:

Average of the number problems which are processing in s-th knot:

Average number of the problems which are queueing to s knot:

Average time of being processing on the s-th knot:

Average for the problem to wait on s-th knot:

Average time of staying in the computing system:

Average waiting time:

Parallel problems processing

The algorithm consists of two parts: calculations of a transitive probabilities matrix and stationary probabilities vector.

Calculation of an element of a transitive probabilities matrix does not depend on the following elements. Therefore, as the main idea of parallel realization of this part of algorithm it is possible to use a principle of parallel processing to [4].

As a base subtask it is possible to take lines, a column or the block of a transitive probabilities matrix calculation. The scheme of parallel algorithm is shown on the figure 3.

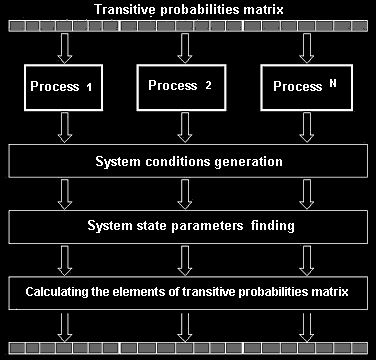
Fig. 3. Parallel algorithm of a transitive probabilities matrix construction

Calculation of stationary probabilities can be realised with the help of iterative algorithm. As the main idea the algorithm of multiplication of a matrix and a vector is used. The scheme calculation algorithm stationary probabilities vector is presented on fig. 4. For parallel processing of matrix multiplication is possible to use ribbon (in the lines or columns) or the block scheme of data division.

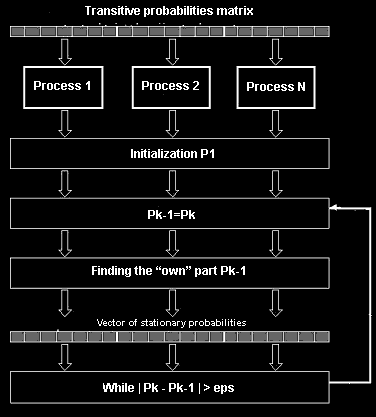
Fig. 4. Parallel algorithm of calculation of a vector of stationary probabilities

Conclusions

In this work the discrete markow’s construction algorithm of a non-uniform clusters is presented. In the future researches we are join to analyse the overall performance efficiency of the considered parallel computer system. Results of modelling can be used for overall performance increase, for synthesis, the analysis, reconfiguration of the cluster systems kind.

Further more this algorithm can be tested on parallel structures of various topology.

Literature

1. Михайлова Т.В. Повышение эффективности кластерных вычислительных систем на основе аналитических моделей. // Автореферат диссертации на соискание ученой степени к.т.н. — Донецк, 2007. — 20 с.
2. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя.— К.:«ДиаСофт», 1998. — 432 с.
3. Фельдман Л.П., Михайлова Т.В. Дискретная модель Маркова однородного кластера // Искусственный интеллект.— Донецк: ІПШІ МОН і НАН України «Наука і освіта», №3, 2006. — http://www.iai.dn.ua/public/JournalAI_2006_3/Razdel2/05_Fel%27dman_Mikhaylova.pdf
4. Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. — http://www.nbuv.gov.ua/portal/natural/Npdntu/ikot/2009_10/09flppmm.pdf

© DonNTU master, Olga Kucherenosova, 2010