Актуальність теми
У зв'язку з неухильним зростанням складності і функціональності приладів, а також необхідності діагностики їх технічного стану методи компактного тестування c локалізацією помилок є одними з найбільш актуальних методів вирішення завдань тестової діагностики. Достоїнством цих методів є значне скорочення обсягу інформації, необхідної для проведення тестового експерименту. При традиційному методі компактного тестування, контроль проводиться за принципом "придатний — не придатний", що є недостатнім у виявленні типу несправності у відмовленному елементі дискретного пристрою. Необхідно і важливо визначити момент часу, коли на виході схеми з'являється помилка, тобто локалізувати помилку у вихідний тестової послідовності бітів. Даний метод дозволяє виявити і визначити тип несправності на підставі отриманих послідовностей бітів, що дозволить прискорити діагностику елементів дискретних пристроїв [1].
Робота присвячена розробленню методики проектування пристроїв компактного тестування з локалізацією помилок і дослідження їх характеристик.
Мета і завдання
Метою даної роботи є розроблення методики проектування пристроїв компактного тестування з локалізацією помилок і дослідження їх характеристик.
Завданнями роботи є огляд існуючих методів локалізації помилок і дослідження їх характеристик для розробки методики проектування пристроїв компактного тестування.
Передбачувана наукова новизна
Передбачувана наукова новизна і плановані практичні результати полягають в отриманні методики проектування пристроїв компактного тестування з локалізацією помилок і дослідження їх характеристик, а також розробка нового і більш оптимального пристрою компактного тестування з локалізацією помилок, яке раніше не розглядалося у різній літературі, або недостатньо повно розглядалося.
Основний зміст роботи
У роботі розглядаються методи компактного тестування з локалізацією помилок у вихідній тестовій послідовності бітів, заснованих на циклічних кодах Хеммінга, Файра, БЧХ, Ріда-Соломона, а також проводиться дослідження їх характеристик.
Циклічні коди Хэммінга
Центральну роль при побудові циклічних кодів грають так звані поліноми, що породжують (утворюючі поліноми). Для циклічних кодів Хеммінга в якості утворюючих використовуються так звані незвідні поліноми.
Незвідним—називається поліном, що не може бути представлений у виді добутку поліномів нижчих степенів (аналогія з простими числами). Незвідні поліноми вибираються з таблиць.
Кількість перевірочних символів циклічного коду дорівнює степені полінома, що породжує, і, навпаки, степінь полінома, що породжує, дорівнює числу перевірочних символів.
Основна ідея циклічного кодування полягає в тім, що дозволене кодове слово повинне ділитися на поліном, що породжує, без залишку.
Залишок від ділення прийнятого декодером кодового слова на поліном, що породжує, виступає в ролі синдрому. Якщо залишок дорівнює нулю, декодер вважає, що помилок не було. У випадку ненульового синдрому в залежності від його виду декодер виконує виправлення помилок.
Розрізняють систематичні і несистематичні циклічні коди.
Приклад систематичного циклічного коду Хеммінга
Вихідні дані:
кількість виправляємих помилок: s=1, dmin=3;
кількість інформаційних символів: k=4;
кількість перевірочних символів: p = [log 2{(k + 1) + [log 2 (k + 1)]}] = 3;
степінь поліному, що породжує: deg K(x) = p = 3;
породжувальний поліном третьої степені: K(x) = х3 + х + 1.
Рисунок 1 — Принципова схема кодера систематичного коду Хеммінга
V — керуючий сигнал;
C — синхросигнал;
R — активний сигнал скидання;
In — інформаційний сигнал;
Out — вихід кодера.
Приклад несистематичного циклічного коду Хеммінга
Вихідні дані:
кількість виправляємих помилок: s=1, dmin=3;
кількість інформаційних символів: k=4;
кількість перевірочних символів: p = [log 2{(k + 1) + [log 2 (k + 1)]}] = 3;
степінь поліному, що породжує: deg K(x) = p = 3;
породжувальний поліном третьої степені: K(x) = х3 + х + 1.
Рисунок 2 — Принципова схема кодера несистематичного коду Хеммінга
C — синхросигнал;
R — активний сигнал скидання;
In — інформаційний сигнал;
Out — вихід кодера.
Декодер Меггітта
Декодер Меггітта виконує не тільки операцію ділення на поліном, що породжує, К(х), але і, як кодер циклічних кодів, операцію множення на поліном х р.
Рисунок 3 — Функціональна схема декодера Меггітта для систематичного (7, 4)-коду Хеммінга з поліномом, що породжує, K(x) = x3 + x + 1.
(Анімація: обсяг - 61.4 КБ; розмір - 628x321, кількість кадрів - 4, затримка між кадрами - 80 мс, затримка між першим і останнім - 320 мс, кількість циклів повторення - нескінчена.)
RG(n=7) — регістр розрядністю 7;
Ind — інформаційний сигнал декодера;
Out(СК) — вихід декодера.
Рисунок 4 — Функціональна схема декодера Меггітта для несистематичного (7, 4)-коду Хеммінга з поліномом, що породжує, K(x) = x3 + x + 1.
RG(n=7) — регістр розрядністю 7;
Ind — інформаційний сигнал декодера;
Out(Н) — вихід декодера [2].
Циклічні коди Файра
Кодуючи пристрої для кодів Файра будуються аналогічно кодуючим пристроям для циклічних кодів Хеммінга. Відмінності полягають у реалізації декодера.
Поліном коду, що породжує, має вигляд:
F(x) = (x 2b-1 + 1)* P(x),
де Р(х) — примітивний поліном, deg P(x) = b, b — довжина пакета помилок, що виправляється. Довжина коду n = (2b - 1)*(2b - 1), кількість перевірочних символів p = 3b – 1, кількість інформаційних символів k = n – p, параметр міри неефективності коду z = b - 1.
Приклад систематичного циклічного коду Файра
Вихідний код (105,94), b=2, g(x)= (х7+1)*(х4+х3+1)=х11+х10+х7+х4+х3+1.
Декодер має вигляд:
Рисунок 5 — Функціональна схема декодера Файра (105,94) для систематичного коду
Приклад систематичного циклічного коду Файра з перемеженням
Вихідний код (105,94), b=2, g(x) = (х7+1)*(х4+х3+1)=х11+х10+х7+х4+х3+1.
j=2, посимвольно перемеженний код (210,188), b=4, g(x) = х22+х20+х14+х8+х6+1.
Декодер має вигляд:
Рисунок 6 — Функціональна схема декодера Файра для систематичного (210,188) коду з перемеженням j = 2
Методом посимвольного перемеження ступеня j можна одержати більш довгі коди, що виправляють пакети помилок довжини (j*b). При цьому, якщо вихідний код має параметри (n,k) і поліном, що породжує, g(x), то новими параметрами будуть (jn, jk) и g(xj) відповідно [2].
Функціональна схема декодера Файра для несистематичної коду будується подібно, як і для коду Хеммінга.
Циклічні коди БЧХ (Боуза – Чоудхурі – Хоквінгема)
Кодуючи пристрої для кодів БЧХ будуються аналогічно кодуючим пристроям для циклічних кодів Хеммінга. Відмінності полягають у реалізації декодера.
Розглянемо на прикладі коду БЧХ (15, 7), що виправляє дві помилки: поліном, що породжує, В(х) = х8 + х7 + х6 + х4 + 1, довжина коду n=15, кількість перевірочних символів p = deg B(x) = 8, кількість інформаційних символів k = 7.
Декодер має вигляд:
Рисунок 7 — Функціональна схема декодера БЧХ для систематичного (15, 7) коду
Декодер працює 3n тактів. Перші n тактів: формується синдром, кодове слово заноситься в буферний регістр. Другі n тактів: виправляється одна з існуючих помилок і кодове слово знову записується в буферний регістр (ключ К – замкнутий), треті n тактів: виправляється друга помилка. Модифікація синдрому для даного коду обов'язкова.
Недоліком даної схемної реалізації є неузгодженість роботи кодера і декодера. Кодер повинен чекати 2n тактів, поки декодер виконає виправлення.
Для усунення цього недоліку використовується конвеєрний варіант реалізації декодера [2].
Метод посимвольного перемеження ступеня j для декодера коду БЧХ будується аналогічно, як і для кодів Файра. А функціональна схема декодера БЧХ для несистематичної коду будується подібно, як і для коду Хеммінга.
Циклічні коди Ріда-Соломона
Коди Ріда-Соломона є окремим випадком кодів БЧХ. Головна відмінність кодів Ріда-Соломона полягає в тому, що в якості символу виступає не двійковий символ (один біт), а елемент поля Галуа (кілька бітів).
Поліном, що породжує коду Ріда-Соломона, а також виправляє s помилок, повинен мати 2s коренів:
{aj0, aj0+1, aj0+2,…, aj0+2s-1},
де j0 – конструктивний параметр. Як правило, j0 вибирають рівним 1. Тоді безліч коренів полінома приймає вигляд {a, a2, a3… a2s}.
Для коду Ріда-Соломона, що виправляє s помилок, поліном, що породжує, має наступний вигляд:
RS(X) = (X - a)(X - a2)(X - a3)…(X - a2s).
При такому уявленні поліном, що породжує, має безліч коренів {a, a2, a3… a2s}.
Суть перешкодостійкого кодування полягає у введенні в первинні коди надмірності. Тому перешкодостійкі коди називають надмірними. Завдання перешкодостійкого кодування полягає в такому додаванні до інформаційних символів первинних кодів додаткових символів, щоб в приймачі інформації могли бути знайдені і виправлені помилки, що виникають під дією перешкод при передачі кодів по каналах зв'язку. Формула обчислення надмірності має вигляд: R=p/n, де p - кількість перевірочних символів, n-довжина коду. Значення p обчислюється за наступною формулою p=degRS(X)=2*s.
Довжина пакету помилок, що виправляється, для послідовного коду без яких-небудь обмежень рівна t=j*b-(b-1) для посимвольного перемеженого коду Ріда-Соломона поля Галуа GF(2b) з параметром перемеження j [8].
Схему посимвольно перемеженого коду Ріда-Соломона можно отримати зі схеми початкового коду, вставивши додатково до кожного елементу пам'яті j-1 елементів. Наприклад, для поля GF(23) при перемежені з параметром j=2 кожну тріаду елементів пам'яті потрібно замінити двома послідовно включеними тріадами [10].
Щоб з (n, k)-кода отримати (jn, jk)-код, виберемо з початкового коду j довільних кодових слів і укрупнимо кодові слова, чередуючи їх символи. Якщо початковий код виправляв довільний пакет помилок довжини d, то, очевидно, результуючий код виправлятиме всі пакети помилок довжини jd. Наприклад, застосовуючи метод перемеження до чотирьох копій (31, 25)-кода, що виправляє пакет помилок довжини 2, отримуємо (124, 100) - код, який може виправляти пакет помилок довжини 8[3].
Припустимо, що початковий код породжується поліномом g(X). Тоді поліном отримуваного перемеженого коду, що породжує, рівний g(Xj). Відмітимо, що перемеженням символів декількох інформаційних поліномів з подальшим множенням на g(Xj) дає те ж саме кодове слово, що і множення кожного з початкових інформаційних поліномів на g(X) з подальшим перемеженням цих слів (n, k)-кода [4].
На рисунках 8-9 представлені приклади схемної реалізації декодерів кодів Ріда-Соломона з полем Галуа GF(8) и GF(16), що виправляють одиночні помилки.
![Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(8) при s=1 [9]](../diss/decoderru.gif)
Рисунок 8 — Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(8) при s=1 [9]
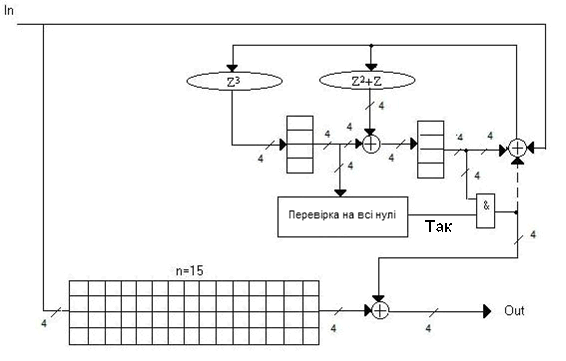Рисунок 9 — Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(16) при s=1
На рисунку 10 представлений приклад схемної реалізації декодера коду Ріда-Соломона з полем Галуа GF(16), що виправляє подвійні помилки.
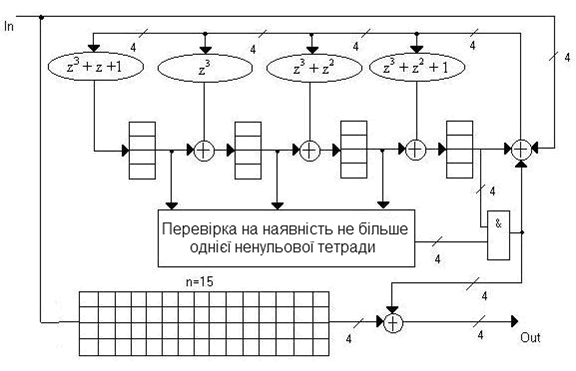Рисунок 10 — Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(16) при s=2
На рисунку 11 представлений приклад схемної реалізації декодера коду Ріда-Соломона з полем Галуа GF(8) і перемеженням j=2, що виправляє одиночні помилки.
![Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(8) і j=2 [9]](../diss/decoderr3u.gif)
Рисунок 11 — Функціональна схема декодера коду Ріда-Соломона для поля Галуа GF(8) і j=2 [9]
Пристрій компактного аналізу
Пристрій компактного аналізу (ПКА) з локалізацією пакетів помилок завдовжки b може бути побудований на основі декодера вибраного коду. Якщо (ПКА) побудовано на основі циклічного n, k-кода (n - довжина коду, k - число інформаційних символів коду, n-k - число перевірочних символів коду), то в якості компактної оцінки виступає залишок від ділення аналізованої послідовності, представленої в поліноміальной формі і помноженої на поліном xn-k, на породжуючий поліном g(x) коду. Якщо ПКА побудоване на основі укороченого n-i, k-i-кода, компактною оцінкою є залишок від ділення аналізованої послідовності, представленої в поліноміальной формі і помноженої на поліном xn-k+i, на поліном, що породжує g(x) кода. Операції множення і ділення поліномів у ПКА реалізуються на регістрах зрушення з лінійними зворотними зв'язками [3,5,6]. Достоїнствами застосування укорочених циклічних кодів для цілей компактного аналізу є скорочення часу локалізації пакету помилок, можливість застосування УКА для різних довжин аналізованої послідовності, забезпечення принципової можливості застосування кодів Файра для локалізації великих пакетів помилок [1,7].
Перш ніж перейти до порівняльного аналізу кодів, сформулюємо критерії ефективності їх застосування для цілей компактного тестування. Ці критерії і показники, що їх характеризують, виходять з вимог, що пред'являються до пристроїв компактного аналізу: довжина сигнатури і апаратні витрати повинні бути мінімальними; довжина аналізованої послідовності повинна бути прийнятною (не менше необхідної довжини, але не дуже великий); швидкодія повинна бути максимальною [1,7].
Методика проектування пристроїв компактного тестування (УКТ) має на увазі наступні етапи:
–аналіз об'єкту діагностики (тип пристрою (комбінаційний, послідовностний, одновивідний або багатовивідний), тип тестування (зондове, пристрій вбудованого контролю), справний або завідомо несправний, помилки викликані переміжними несправностями, постійними несправностями, випадковими збоями, характер розподілу помилок різної кратності );
–аналіз тестових впливів (вичерпне тестування (комбінаційні схеми), псевдовипадкове тестування, синтезовані тести, випадкові тести та ін.) Для синтезованих тестів ймовірність помилки малої кратності максимальна. Для переміжних несправностей ймовірність одиночних помилок максимальна. Для свідомо справних об'єктів ймовірність одиночного збою максимальна, при цьому при повторному тестуванні виявлення може бути різним;
–вибір коду для реалізації компактного тестування.
Для випадкових збоїв і переміжних несправностей досить вибрати код Хеммінга. Для постійних несправностей доцільно використовувати коди, що виправляють пакунки помилок (коди Файр або коди Ріда-Соломона). Всі ці коди відносяться до блокових кодів. Деревовидні коди для цих цілей незастосовують. Крім того, незастосовують для цих цілей такі коди, як наприклад турбо-коди, які хоча і є блоковим, для них використовуються методи кодування, розроблені для деревовидних кодів;
–розробка УКТ на основі циклічних блокових кодах.
Основа УКТ — декодер вибраного коду без буферного регістра не конвеєрної реалізації. Для локалізації помилок використовується лічильник. Перед стисканням тестових реакцій, еталонна сигнатура завантажується в генератор синдрому. У деяких випадках не для укорочених кодів доцільна альтернативна реалізація генератора синдрому (схема розподілу полінома із зовнішніми суматором в ланцюгах зворотнього зв'язку). Залежно від довжини тесту використовуються декодери для укорочених або не укорочених кодів;
–отримання еталонних компактних оцінок.
Еталонні компактні оцінки розраховуються або аналітично, або формуються за допомогою свідомо справного пристрою і кодера обраного коду. Завантаження еталонної послідовності УКТ може вироблятися або паралельним, або послідовним способом, як до початку тестування, так і після, головне щоб виконувався принцип суперпозиції, тобто при збігу компактних оцінок результат посімвольного складання нуль, а при неспівпаданні відмінний від нуля.
–аналіз характеристик різних реалізацій кодів.
Приміром, коди Ріда-Соломона. Опис характеристик можна подивитися за наступними посиланнями [4,,
8,
10].
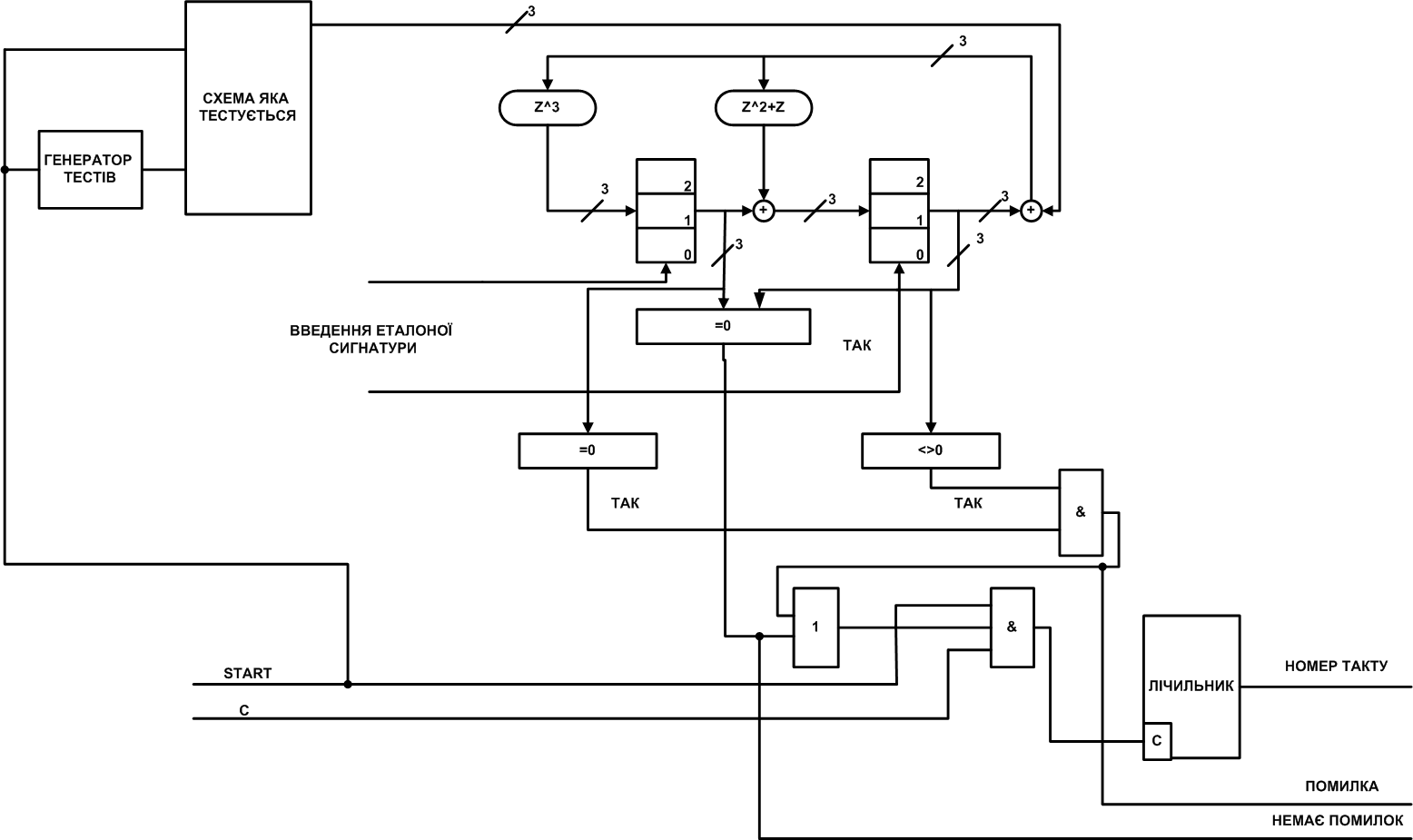Рисунок 12 — Функціональна схема УКТ заснована на декодері коду Ріда-Соломона для поля Галуа GF (8)
Опис роботи функціональної схеми УКТ наведеною на рисунку 12
Робота схеми починається з введення еталонної сигнатури в елементи пам'яті генератора синдрому Ріда-Соломона, потім по сигналу Start запускається генератор тестів і тестована схема. Генератор тестів посилає тестову послідовність на тестовану схему. Реакція тестованої схеми подається на генератор синдрому Ріда-Соломона, де відбувається ділення на поліном, що породжує, і посімвольное складання з еталонної сигнатурою. Потім відбувається перевірка бітів з генератора синдрому Ріда-Соломона на нуль, якщо так (усі нулі), то видається сигнал немає помилок, інакше при виявленні в одному блоці елементів пам'яті нульове значення, а в іншому не нульове значення в такому порядку, як показано на схемі, то видається сигнал про помилку і лічильник припиняє свою роботу на номері того такту, коли відбулася помилка.
Висновок
Таким чином, використовуючи термінологію перешкодостійкого кодування, ефективність застосування кодів для цілей компактного тестування слід порівнювати за наступними показниками. По-перше, число перевірочних символів n-k коду повинне бути мінімальним, в цьому випадку довжина сигнатури і апаратні витрати також будуть мінімальними. По-друге, довжина коду n, відповідна довжині аналізованої послідовності, повинна бути достатньо великою [1].
Список літератури
1. Дяченко О.Н. Компактное тестирование запоминающих устройств с локализацией пакетов ощибок // Электрон. моделирование.- 1996.- 18, №6.- С.43-48.
2. Дяченко О.М. Теорія інформації та кодування // Електронний конспект лекцій.-2008.
3. Блейхут Р. Теория и практика кодов, контролирующих ошибки / Пер. с англ. - М.: Мир, 1986. - 576 с.
4. Юрьев И.В., Дяченко О.Н. Определение оптимальных параметров кодов Рида-Соломона // Інформатика та комп'ютерні технології / Матеріали V міжнародної науково-технічної конференції студентів, аспірантів та молодих науковців - 24-26 листопада 2009 р., Донецьк, ДонНТУ. - 2009. - С. 82-88.
5. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки / Пер. с англ. - М.:Мир, 1976. - 575 с.
6. Касами Т., Токура Н., Ивадари Е., Инагаки Я. Теория кодирования / Пер. с яп. - М.: Мир, 1978.-576 с.
7. Dyachenko O.N. Memory Compact Testing with Error Burst Localization// Engineering Simulation.- 1997.- Vol.14.- pp.907-915. (0,63 др. арк.)
8. Дяченко О.Н. Аппаратная реализация и корректирующие возможности кодов Рида-Соломона // Наукові праці Донецького національного технічного університету. Серія "Проблеми моделювання та автоматизації проектування динамічних систем" (МАП-2007). Випуск: 6 (127) - Донецьк: ДонНТУ. - 2007. - С.113-121. [Электронный ресурс] &mdash Режим доступа: http://www.nbuv.gov.ua/portal/natural/Npdntu/Pm/2007/07donrsc.pdf
9. Дяченко О.Н. Компактный анализ над полем GF(3) // Наукові праці Донецького національного технічного університету. Серія: Проблеми моделювання та автоматизації проектування динамічних систем (МАП-2002). Випуск: 52.- Донецьк: ДонНТУ.- 2002.-С.162-167. (0,38 др. арк.)
10. Юрьев И.В., Дяченко О.Н. Влияние параметров поля Галуа и перемежения на избыточность кода Рида-Соломона // Інформаційні управляючі системи та комп'ютерний моніторинг (ІУС та КМ-2010) / Матеріали I всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених - 19-21 травня 2010 р., Донецьк, ДонНТУ. - 2010. - С. 164-168.
Примітка
При написанні даного автореферату магістерська робота ще не завершена. Дата остаточного завершення роботи: грудень 2010 р. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його наукового керівника після вказаної дати.
| 
